Kapilarni fenomeni (fizika). Kapilarni fenomeni u prirodi

Među procesima koji se mogu objasniti pomoću površinske napetosti i vlaženja tekućina, valja istaknuti kapilarne pojave. Fizika je misteriozna i izvanredna znanost, bez koje bi život na Zemlji bio nemoguć. Pogledajmo najživlji primjer ove važne discipline.

U životnoj praksi, takva zanimljiva sa stajališta fizičkih procesa, kao što su kapilarne pojave, vrlo su česta pojava. Činjenica je da smo u svakodnevnom životu okruženi mnogim tijelima koja lako upijaju tekućinu. Razlog tome je njihova porozna struktura i elementarni zakoni fizike, a rezultat su kapilarne pojave.

Uska cijev

Kapilara je vrlo uska cijev u kojoj se fluid ponaša na poseban način. Mnogo je primjera takvih žila u prirodi - kapilara cirkulacijskog sustava, poroznih tijela, tla, biljaka itd.

Kapilarni fenomen je podizanje ili spuštanje tekućina duž uskih cijevi. Takvi se procesi promatraju u prirodnim kanalima ljudi, biljaka i drugih tijela, kao iu posebnim uskim staklenim posudama. Slika pokazuje da su u cijevima za komunikaciju različite debljine uspostavljene različite razine vode. Primijećeno je da što je posuda tanja, to je viša razina vode.

Ti fenomeni leže u osnovi upijajućih svojstava ručnika, ishrane biljaka, kretanja tinte duž jezgre i mnogih drugih procesa.

Kapilarni fenomeni u prirodi

Gore opisani proces izuzetno je važan za održavanje biljnog svijeta. Tlo je dosta labavo, između njegovih čestica postoje praznine, koje su kapilarna mreža. Voda se uzdiže uz ove kanale, hrani korijenski sustav biljaka vlagom i svim potrebnim tvarima.

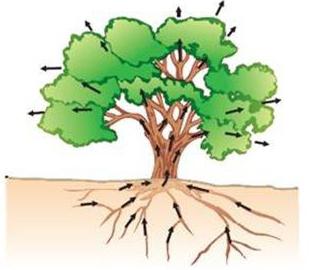
Za iste kapilare, tekućina aktivno isparava, pa je potrebno oranju zemlje, koja će uništiti kanale i zadržati hranjive tvari. I obrnuto, prešano tlo će brže isparavati vlagu. To objašnjava važnost obrađivanja tla kako bi se zadržale podzemne vode.

U biljkama kapilarni sustav osigurava porast vlage od malih korijena do najgornjih dijelova, a kroz lišće isparava u vanjsko okruženje.

Površinska napetost i vlaženje

U središtu pitanja ponašanja tekućine u posudama su fizički procesi kao površinska napetost i vlaženje. Njihove kapilarne pojave proučavaju se u kombinaciji.

Pod djelovanjem sile površinske napetosti, tekućina za vlaženje u kapilarama je iznad razine na kojoj bi trebala biti u skladu sa zakonom koji se odnosi na posude. Suprotno tome, tvar koja se ne vlaži nalazi se ispod te razine.

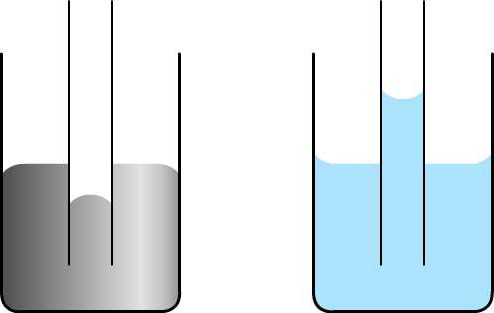
Tako se voda u staklenoj cijevi (tekućina za kvašenje) podiže na veću visinu, a tanjim je posuda. Naprotiv, živa u staklenoj epruveti (tekućina koja ne vlaži) spušta se niža, što je taj kapacitet tanji. Osim toga, kao što je prikazano na slici, tekućina za vlaženje oblikuje konkavni oblik meniska, a nevlaženje - konveksno.

vlaženje

To je fenomen koji se javlja na granici gdje tekućina dolazi u dodir s krutinom (druga tekućina, plinovi). Nastaje zbog posebne interakcije molekula na granici njihovog kontakta.

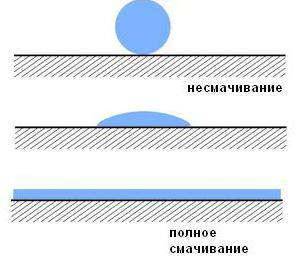
Potpuno vlaženje znači da se kapljica širi po površini krute tvari, a nevlaženje pretvara u sferu. U praksi se ovaj ili onaj stupanj vlaženja češće susreće nego ekstremne opcije.

Sila površinske napetosti

Površina kapljice ima sferni oblik, a razlog tome je zakon koji djeluje na tekućinu, površinsku napetost.

Fenomen kapilara je posljedica činjenice da konkavna strana tekućine u cijevi nastoji poravnati do ravnog stanja zbog sila površinske napetosti. To je popraćeno činjenicom da vanjske čestice nose tijela ispod njih gore s njima, a tvar se uzdiže do cijevi. Međutim, tekućina u kapilari ne može poprimiti ravan oblik površine, a taj se proces podizanja nastavlja do određenog trenutka ravnoteže. Da biste izračunali visinu na kojoj se vodeni stupac diže (pada), trebate koristiti formule koje će biti prikazane u nastavku.

Izračun visine uspona vodenog stupca

Trenutak zaustavljanja porasta vode u uskoj cijevi dolazi kada gravitacija P tvari tvari uravnotežuje silu površinske napetosti F. Ovaj trenutak određuje visinu porasta tekućine. Kapilarne pojave nastaju zbog dvije različito usmjerene sile:

• gravitacija P uzrokuje da se tekućina spusti;
• sila površinske napetosti F pomiče vodu prema gore.

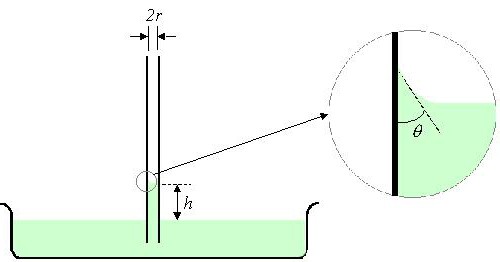
Sila površinske napetosti koja djeluje oko oboda, gdje je tekućina u dodiru sa stijenkama cijevi, jednaka je:

F = σ2πr,

gdje je r polumjer cijevi.

Težina koja djeluje na tekućinu u cijevi je:

P ty = ρπr2hg,

pri čemu je ρ gustoća tekućine; h je visina stupca tekućine u cijevi;

Dakle, tvar će prestati rasti, pod uvjetom da je P _teška = F, što znači da

ρπr ² hg = σ2πr,

stoga je visina fluida u cijevi jednaka:

h = 2σ / pqr.

Slično za tekućinu koja ne vlaži:

h je visina spuštanja tvari u cijevi. Kao što se može vidjeti iz formula, visina na koju se voda uzdiže u uskoj posudi (ponorima) obrnuto je proporcionalna radijusu spremnika i gustoći tekućine. To se odnosi na tekućinu za vlaženje i nevlaženje. Pod drugim uvjetima potrebno je napraviti izmjenu u skladu s oblikom meniskusa, što će biti prikazano u sljedećem poglavlju.

Laplaceov tlak

Kao što je već napomenuto, tekućina u uskim cjevčicama ponaša se na takav način da daje dojam kršenja zakona komuniciranja posuda. Ta činjenica uvijek prati kapilarne pojave. Fizika to objašnjava uz pomoć Laplaceovog tlaka, koji je usmjeren prema gore s tekućinom za vlaženje. Stavljajući vrlo usku cijev u vodu, promatramo kako se tekućina povlači na određenu razinu h. Prema zakonu o komuniciranju plovila, morao je biti uravnotežen s vanjskom razinom vode.

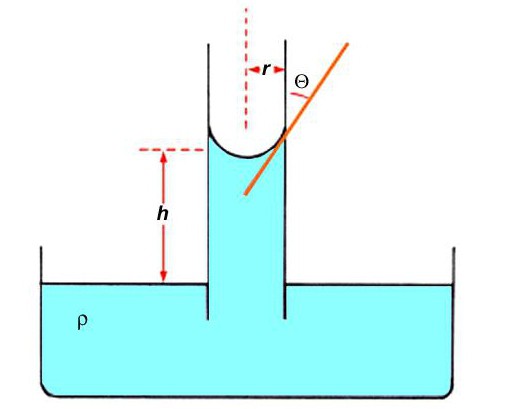
Ovo odstupanje se objašnjava smjerom Laplaceovog tlaka p _l :

p _l = 2σ / R,

U ovom slučaju, usmjeren je prema gore. Voda se uvlači u cijev do razine gdje dolazi do uravnoteženja s hidrostatskim tlakom p _g vodenog stupca:

pg = pqh

i ako je p _l = p _g , onda možete izjednačiti dva dijela jednadžbe:

2σ / R = pqh.

Sada je visinu h lako izvesti kao formulu:

h = 2σ / pqR.

Kada je vlaženje dovršeno, onda je meniskus, koji formira konkavnu površinu vode, u obliku polukugle, gdje je 0 = 0. U tom slučaju, radijus kugle R će biti jednak unutarnjem radijusu kapilare r. Odavde dobivamo:

h = 2σ / pqr.

A u slučaju nepotpunog vlaženja, kada je,, 0, radijus sfere može se izračunati pomoću formule:

R = r / cosƟ.

Tada će željena visina, koja ima ispravak za kut, biti jednaka:

h = (2σ / pqr) cos .

Iz prikazanih jednadžbi može se vidjeti da je visina h obrnuto proporcionalna unutarnjem radijusu cijevi r. Voda doseže svoju maksimalnu visinu u posudama koje imaju promjer ljudske kose, koje se nazivaju kapilare. Kao što znate, tekućina za vlaženje je izvučena i tekućina koja se ne vlaži potiskuje se dolje.

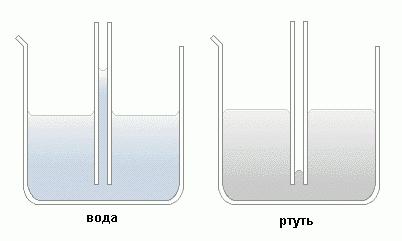
Eksperiment možete provesti uzimanjem posudica koje komuniciraju, gdje je jedna od njih široka, a druga vrlo uska. Nakon što se ulije u vodu, moguće je uočiti različitu razinu tekućine, au varijanti s vlažnom tvari razina u uskoj cijevi je viša, a kod ne-vlažnog niža.

Važnost kapilarnih fenomena

Bez kapilarnih pojava, postojanje živih organizama jednostavno je nemoguće. Ljudsko tijelo preko najmanjih posuda prima kisik i hranjive tvari. Biljke korijena - mreža kapilara, koji vuče vlagu iz tla, dovodeći ga do vrha lišća.

Jednostavno kućno čišćenje nije moguće bez kapilarnih fenomena, jer na tom principu tkanina upija vodu. Ručnik, tinta, fitilj u uljanoj svjetiljci i razni uređaji rade na toj osnovi. Kapilarne pojave u tehnologiji igraju važnu ulogu u sušenju poroznih tijela i drugih procesa.

Ponekad te iste pojave uzrokuju nepoželjne posljedice, na primjer, pore opeke upijaju vlagu. Da biste izbjegli vlagu zgrada pod utjecajem podzemnih voda, morate zaštititi temelj hidroizolacijskim materijalima - bitumenom, krovnim filcem ili krovnim papirom.

Drenaža odjeće na kiši, primjerice, hlače do koljena od hodanja po lokvama također je posljedica kapilarnih fenomena. Postoje mnogi primjeri ovog prirodnog fenomena oko nas.

Eksperimentirajte s cvijećem

Primjeri kapilarnih fenomena mogu se naći u prirodi, pogotovo kada su u pitanju biljke. Njihovi debla imaju mnogo malih posuda unutra. Možete provesti eksperiment s bojanjem cvijeća u bilo kojoj svijetloj boji kao rezultat kapilarnih fenomena.

Morate uzeti vedro obojenu vodu i bijeli cvijet (ili Pekinški list kupusa, stabljiku celera) i staviti ga u čašu s ovom tekućinom. Nakon nekog vremena na lišću pekinškog kupusa može se vidjeti kako se boja kreće prema gore. Boja biljke će se postupno mijenjati u skladu s bojom u kojoj se nalazi. To je zbog kretanja tvari prema stablima prema zakonima koje smo razmatrali u ovom članku.