Primjer algoritma Diffieja Hellmana

Objavljivanje teme kriptografije s javnim ključem mora započeti povijesnim putem problema. Whitfield Diffie i Martin Hellman prvi su pitali o otvorenoj metodi predaje ključeva. To se dogodilo 1976. Publikacija je napravila prve pokušaje rješavanja problema. Njihovo rješenje nije bilo bez nedostataka, već je postavilo temelje za potpuno drugačiji način razmišljanja u području šifriranog prijenosa podataka.

Preduvjeti za stvaranje Diffie-Hellmanova algoritma

Do ovog trenutka autentifikacija i šifriranje bili su mogući samo putem zajedničkog tajnog ključa. S razvojem tehnologije, pitanje je postalo sve akutnije. Ako 10 osoba treba međusobno prenijeti podatke preko nesigurnih kanala, morat će međusobno razmjenjivati ​​lozinke. Ovaj zadatak izgleda posve stvaran. Čak is potrebom da ih ažurirate. Uostalom, za 10 prijatelja trebat će vam samo 45 tajnih ključeva. A ako će kontakti biti 100? Trebat će 4950 zaporki. Situacija raste kao gruda snijega.

Glavno postignuće Diffieja i Hellmana bilo je ispravno formuliranje pitanja i genijalni odgovor na njega. Predložili su da se podaci mogu šifrirati na jedan način i dešifrirati u drugom. To jest, imati 2 ključa. Onaj koji se koristi za enkripciju može ostati otvoren. Dakle, svaka osoba može šifrirati poruku, ali samo vlasnici drugog tajnog ključa mogu je dešifrirati. Ali kako implementirati algoritam za prijenos takvog ključa? Znanstvenici su mogli djelomično i dati odgovor.

Kratka matematika: skupine

Diffie-Hellmanov algoritam ili protokol (dalje DH) radi uz pomoć jednostavnih brojeva. Neka je dovoljno velik broj koji pripada skupu prosti brojevi. Algoritam uključuje korištenje više od 250-500 bajtova. Neka Za bude multiplikativna skupina prstenastog prstena po modulu a, koji će se koristiti pomoću Diffie-Hellmanova algoritma enkripcije. Sastoji se od skupa brojeva 1, ..., a-1.

Uzmite neki element b iz grupe Z a razmislite o beskonačnom nizu 1, b, b ² , b ³ , b ⁴ , ... Iz činjenice da je skupina Z _a po definiciji konačni skup, prije ili kasnije razmatrani slijed {b} će se početi ponavljati. Postavite b ⁱ = b ^j (i <j).

Sada dijelimo svaki dio jednakosti s b ⁱ (modulo a) i dobivamo b ^ji = 1. To znači da postoji broj k = ji za koji je b ^k = 1 (mod a) istinit. Najmanji k za koji ta jednakost vrijedi naziva se redoslijed b. Da bi se izbjegla zabuna s drugom posebnom literaturom, standardna matematička notacija koristi se za objašnjenje Diffie-Hellmanova sustava.

Dakle, podizanjem broja b, koji se naziva generirajući element, na snagu dobivamo niz brojeva (set) 1, ..., b ^k-1 . Broj elemenata u ovom skupu je točno k.

Svojstvo množenja modulo a kaže da postoji najmanje jedan broj b koji generira sve elemente skupine Z * _a . Drugim riječima, postoji broj za koji je k = a - 1 istinit.Ovo svojstvo nam omogućuje da predstavimo brojeve skupine Z * _a u obliku 1, b, b ² , ... b ^a-2 . Takav broj b se naziva primitivnim brojem grupe.

U nastavku, iz grupnih znakova lako je dokazati da je skup koji generira broj b također i sama grupa i nasljeđuje sva svojstva skupina. Drugim riječima, operacije unutar generirane grupe ili podskupine mogu se izvesti na točno isti način kao u grupi modulo a.

Razmotrite izjavu. Za svaki element b njegov red je djelitelj a-1. Lako je pokazati. Neka je a = 7. Broj b = 3 je primitivan, jer 1, ..., b ⁵ = 1, 3, 2, 6, 4, 5. Tada će broj h = 2 generirati podskupinu 1, ..., h ² = 1 , 2, 4, budući da h ³ = 2 ³ mod 7 = 1. h = 6 generira podskupinu 1, 6. Veličine grupa su 3, odnosno 2. Očito, to su djelitelji broja a-1 = 6.

Prvi DH algoritam

U izvornoj verziji, algoritam je radio kako slijedi. Veliki broj a se bira iz skupa jednostavnog i primitivnog elementa b koji generira Z * _a . Oba broja a i b predstavljaju javni ključ, oni su poznati svima, uključujući i napadače. Kako onda sakriti poruke?

U tom su koraku Diffie i Hellman došli do vrlo genijalnog poteza. Pretpostavimo da imamo dvije osobe koje međusobno komuniciraju: A i B. Prvo, A bira slučajni broj x iz Z * _a , koji je ekvivalentan odabiru broja iz {1, ..., a-1}. Zatim izračunava vrijednost pomoću formule (b ^x mod a) i šalje je B. Naizmjence, B bira određeni broj y iz istog skupa, izračunava vrijednost (b ^y mod a) i šalje rezultat natrag A.

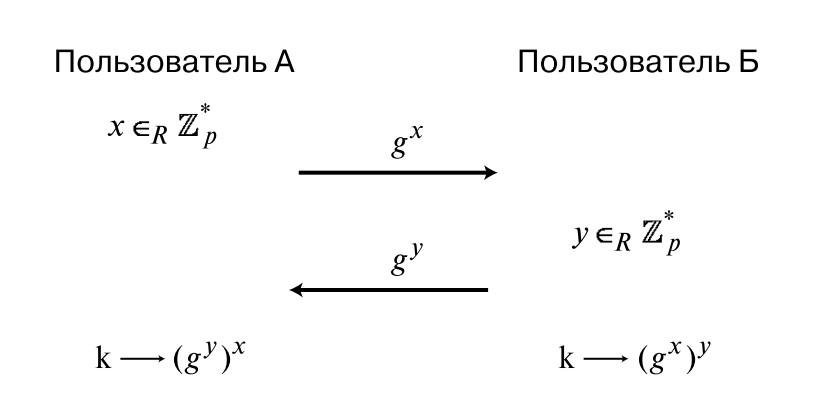
Na tako lukav način, ispada da tajni ključ izgleda b ^xy . Zbog svojstva stupnjeva, koji kaže g ^xy = (g ^y ) ^x , sugovornik A može izračunati željenu vrijednost i dešifrirati informacije koje su mu poslane. I na isti način, ovu vrijednost izračunava sugovornik B. Dakle, oboje imaju isti tajni ključ.

Koje probleme namjernik doživljava s tom razmjenom informacija? On može presresti brojeve g ^x i g ^y . Čak i uz poznavanje javnih ključeva, problem izračunavanja g ^xy nije trivijalan, t. Budući da ne postoji učinkovit algoritam za pronalaženje željene vrijednosti u distribuciji Diffie-Hellmanovih ključeva. Ovaj problem poznat je kao problem računanja diskretnog logaritma.

Napad posrednika

Jedna od slabosti primarnog Diffie-Hellmanova algoritma je njegova ranjivost na posredne napade. Što to znači? Sugovornik A zna da komunicira s određenim licem, ali s kim konkretno - nema pojma. Tako napadač može intervenirati u prijenosu informacija i oponašati sugovornika B kada komunicira s A, i obrnuto. Nitko od njih neće moći sumnjati da nešto nije u redu.

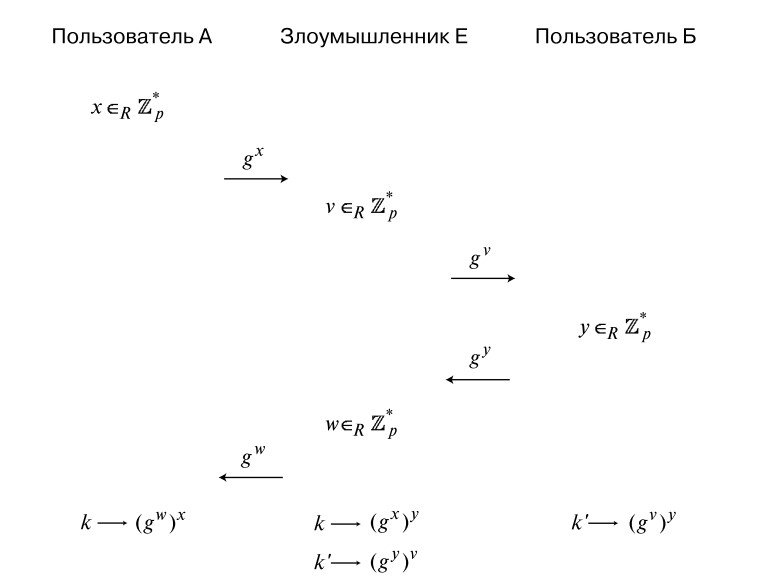
Postoji samo jedno područje uporabe u kojem su isključeni napadi na Diffie-Hellmanov algoritam. Ovo je telefonski i videopoziv. Ovdje se sugovornici mogu međusobno poznavati, tako da posrednik neće moći prodrijeti.

zamke

Osim napada posrednika, DH protokol sadrži i niz drugih problema. Na primjer, jedan od nedostataka je slučaj kada primitiv nije primitivan. Tada generira samo podskupinu. Zbog sužavanja broja mogućih opcija, napadač otvara mogućnost pretraživanja.

Problemi zbog ovog nedostatka mogu se izbjeći ako svaki od sugovornika provjeri jesu li brojevi a i b ispravni prije početka razmjene podataka. To jest, a je prost broj i b je primitivan. Međutim, kada je riječ o sigurnosti kroz implementaciju određenih uniformnih, opcionalnih koraka, korisnici ih često ignoriraju.

Drugi ozbiljan problem nastaje na temelju podgrupa modulo a. Ako napadač odabere da promijeni g ^x na 1 kako bi mu bilo lakše prisluškivati, korisnici ga mogu lako detektirati provjerom broja za utakmicu. Međutim, ako zamijeni ključ s niskim brojem narudžbe, korisnici neće moći ništa posumnjati. A budući da će broj elemenata u skupu s niskim redoslijedom biti mali, napadač će morati izdvojiti mali broj opcija za dekodiranje.

Pouzdanost prostih brojeva

DH algoritam koristi veliki i pouzdan broj mnogih jednostavnih. Kako točno odabrati? Analiziramo korake.

1. Pomoću formule a = 2k + 1 odaberite brojeve a i k tako da su jednostavni.
2. Iz skupa 1, ..., a-1 isključimo 1 i a-1.
3. Uzmite slučajni broj x iz skupa preostalog nakon drugog koraka i pronađite vrijednost b = x ² (mod a).
4. Provjerite je li b jednak 1 ili a-1. Ako je b jednaka jednoj od zabranjenih vrijednosti, trebate odabrati drugi x. I ponovite operaciju.

Skup (a, k, b) dobiven na ovaj način može se smatrati dovoljnim za upotrebu u Diffie-Hellmanovom algoritmu razmjene ključeva. U skladu s tim, primatelj poruke također treba provjeriti vrijednost, koja mora biti snaga b, i provjeriti (primjerice, funkciju Legendre simbola) da pada u skup koji generira broj b.

Korištenje podskupina

Glavni nedostatak gore navedenog algoritma je nedovoljna učinkovitost. Uz pretpostavku da je duljina prostog broja a n bita, tada je k n-1 bita. Pokazalo se da će svi stupnjevi biti dugi n-1. Zatim operaciju eksponenciranje u prosjeku će se sastojati od 3n / 2 množenja mod a. Ovo je veliki proces.

Kako bi se nosili s ovim problemom, odlučeno je da se koriste manje podskupine. Kakav je učinak u ovom slučaju? Ako se broj a sastoji od 2000 bita, tada je potrebno 3000 operacija množenja za izračunavanje b ^x . Korištenjem podskupina, taj se broj može smanjiti na ~ 400. Ovo značajno povećanje učinkovitosti algoritma omogućuje njegovu punu primjenu. Na primjer, algoritam Diffie-Hellman s tri ili više članova.

Što bi trebalo biti duljina a

Pravilan odabir veličina parametara Diffie-Hellmanova algoritma prilično je složen zadatak. Uobičajeni zahtjev u svijetu kriptografije je, primjerice, uvjet da napadač treba najmanje ^2.128 koraka kako bi provalio u sustav. Ako je u simetričnim algoritmima šifriranja u skladu s takvim zahtjevom vrlo jednostavno, u algoritmima s javnim ključem to je pravi problem. Ako ispunjavate gore navedeni zahtjev, duljina a mora se sastojati od najmanje 850 bajtova.

U praksi, ova veličina stvara velike probleme u performansama u sustavu, budući da operacije s javnim ključem traju mnogo dulje nego, na primjer, u simetričnom kodiranju s 128 ili 256 bitnim ključevima. Kako onda biti? Minimalna duljina javnog ključa mora započeti s 2048 bita. Iako je ključ duži, viša je razina sigurnosti. Treba razmotriti prvenstveno rad sustava i njegovu cijenu. Ako vam dopušta korištenje ključa od 4096 bita, morate to učiniti.

Kako se procjenjuje potrebna razina sigurnosti?

Veličina ključa u simetričnom šifriranju ostaje nepromijenjena (128, 256 bita) cijeli život sustava, dok su veličine javnog ključa uvijek varijabilne vrijednosti. Ako morate razviti sustav koji se mora koristiti 30 godina i čuvati podatke u tajnosti najmanje 20 godina nakon što je sustav izvađen iz upotrebe, tada veličina simetričnog ključa za šifriranje u početku mora biti dovoljno velika da zaštiti sustav za sljedećih 50 godina.

Zbog očitih problema s performansama, zbog činjenice da Diffie-Hellmanov algoritam šifrira mnogo više operacija, zahtjevi za javne ključeve se razlikuju. I dalje vrijedi godinu dana i štiti podatke za sljedećih 20 godina, odnosno koristi se ukupno 21 godinu. Zbog varijabilne veličine ključ se može mijenjati svake godine i stvarati sve duže kako bi se osigurala potrebna razina sigurnosti.

Na primjer, najbolje procjene pokazuju da ključ s duljinom od 256 bajtova može zaštititi podatke tijekom 20 godina, duljina od 384 bajta je 35 godina, a duljina 512 bajta je 47 godina, itd. Broj je 6800 bita, čime se osigurava da napadač Potrebno je ^2.128 koraka kako bi se ispucao, izveden iz sličnih procjena. Međutim, ovo je samo predviđanje, koje morate s velikom pažnjom vjerovati. Možete prilično točno predvidjeti razvoj događaja za 10 godina unaprijed, ali na 50 - to je fantastično.

Praktične preporuke

Evo nekoliko praktičnih savjeta o korištenju DH protokola. Odaberite k kao prost broj od 256 bita. To je minimum koji može pružiti barem neku adekvatnu razinu sigurnosti od napada. Za a, odaberite broj koji bi imao oblik Na + 1, gdje je N cijeli broj. O veličini broja a rečeno je ranije. Nakon toga, odabire se slučajni broj b i provjerava se za nekoliko uvjeta. Prvo, ne može biti jedinica. Drugo, b ^k = 1.

S druge strane, svaki sudionik u komunikaciji treba biti uvjeren u sljedeće:

• a i k su prosti brojevi, duljina k je 256 bita, duljina p je prilično velika.
• broj k je djelitelj a-1.
• b nije jednak 1 i b ^k = 1.

Ove uvjete treba provjeriti i uz bezuvjetno povjerenje u izvor.

zaključak

DH algoritam je genijalno rješenje jednog od ozbiljnih problema i još uvijek se aktivno koristi u modificiranom obliku za moderne sigurnosne zahtjeve u različitim protokolima. Diffie-Hellmanov algoritam, na primjer, koristi se u nekim dijelovima implementacije IKE protokola. Međutim, njegova uporaba trebala bi biti metodična i oprezna zbog prisutnosti očitih problema i ozbiljnih zamki.