Kako izračunati opseg i opseg kruga?
Okolnost se nalazi u svakodnevnom životu ne manje od pravokutnika. I mnogi ljudi imaju problem kako izračunati duljina opsega uzrokuje poteškoće. I sve zato što nema uglova. Uz njihovu prisutnost, sve bi bilo mnogo lakše.
Što je krug i gdje se to događa?
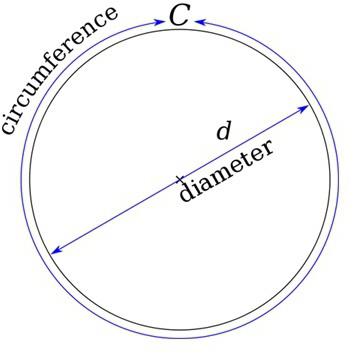
Ta ravna figura predstavlja više točaka koje se nalaze na istoj udaljenosti od druge, koja je središte. Ta se udaljenost zove radijus.
U svakodnevnom životu nije često potrebno izračunavati opseg, osim ljudi koji su inženjeri i dizajneri. Oni stvaraju nacrte mehanizama koji koriste, na primjer, zupčanike, prozore i kotače. Arhitekti stvaraju kuće koje imaju okrugle ili zasvođene prozore.
Svaki od ovih i drugih slučajeva zahtijeva vlastitu točnost. Štoviše, apsolutno je nemoguće izračunati duljinu opsega. To je zbog beskonačnosti osnovnog broja koji se nalazi u formuli. "Pi" se još uvijek razjašnjava. I najčešće se koristi zaokružena vrijednost. Stupanj točnosti odabire se tako da se dobije najtočniji odgovor.
Označavanje količina i formula
Prije izračuna duljine kruga, morate se dogovoriti o tome što znači slovo. Pogodno je pisati u tablici.
| vrijednost | oznaka |
| radius | r |
| dijametar | d |
| obujam | l |
Sada je lako odgovoriti na pitanje kako izračunati opseg kruga duž radijusa, što će zahtijevati sljedeću formulu:
l = 2π * r.
U nastavku je π zaokrućen. Najčešće zadaci koriste vrijednost 3.14. Ali ponekad je potrebna veća točnost i tada se koristi takav broj: 3.14159.

Budući da su radijus i promjer međusobno povezani, postoji još jedna formula za izračune. Kako je radijus dva puta manji, izraz se malo mijenja. I formula za izračunavanje opsega, znajući promjer, bit će kako slijedi:
l = π * d.
Što ako trebate izračunati opseg kruga?
Samo zapamtite da krug uključuje sve točke unutar kruga. Dakle, njegov se perimetar poklapa s njegovom duljinom. I nakon izračunavanja opsega, stavite znak jednakosti s obodom kruga.
Usput, imaju iste oznake. To vrijedi za radijus i promjer, a perimetar je latinsko slovo P.
Primjeri zadataka
Prvi zadatak
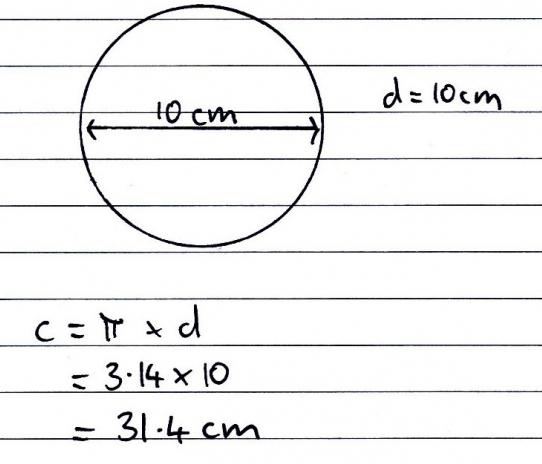
Stanje. Saznajte duljinu kruga čiji radijus iznosi 5 cm.
Odluka. Lako je razumjeti kako izračunati duljinu kruga. Vi samo trebate koristiti prvu formulu. Budući da je radijus poznat, potrebno je samo zamijeniti vrijednosti i brojati. 2 puta radijus od 5 cm će dati 10. Ostaje da se pomnoži s vrijednošću π. 3,14 x 10 = 31,4 (cm).
Odgovor: l = 31,4 cm.
Zadatak dva
Stanje. Postoji kolo, čiji je obujam poznat i jednak je 1256 mm. Potrebno je izračunati njegov radijus.
Odluka. U ovom zadatku trebate koristiti istu formulu. Ali samo poznatu duljinu treba podijeliti na proizvod 2 i π. Ispada da će proizvod dati rezultat: 6.28. Nakon podjele, broj ostaje: 200. To je željena vrijednost.
Odgovor: r = 200 mm.
Treći zadatak
Stanje. Izračunajte promjer ako je opseg poznat, što je 56,52 cm.
Odluka. Slično prethodnom zadatku, trebat ćete podijeliti poznatu duljinu s π vrijednošću, zaokruženu na stotinki. Kao rezultat ove akcije dobiva se broj 18. Rezultat je dobiven.
Odgovor: d = 18 cm.
Četvrti zadatak
Stanje. Ruke sata imaju duljinu od 3 i 5 cm, potrebno je izračunati duljinu krugova koji opisuju njihove krajeve.
Odluka. Budući da se strelice poklapaju s radijusima krugova, potrebna nam je prva formula. Treba je koristiti dvaput.
Za prvu duljinu, proizvod će se sastojati od množitelja: 2; 3.14 i 3. Rezultat će biti broj od 18,84 cm.
Za drugi odgovor trebate pomnožiti 2, π i 5. Proizvod će dati broj: 31,4 cm.
Odgovor: 1 = 18,84 cm, 2 = 31,4 cm.
Peti zadatak
Stanje. Vjeverica teče u kotaču promjera 2 m. Koja udaljenost radi u jednom punom obrtu kotača?
Odluka. Ta je udaljenost jednaka opsegu. Stoga morate koristiti odgovarajuću formulu. Naime, pomnožimo vrijednost π i 2 m. Izračuni daju rezultat: 6,28 m.
Odgovor: Vjeverica teče 6,28 m.