Izobarni proces, srodne jednadžbe i izvođenje formule rada

Izobarni proces (koji se naziva i izobarički proces) jedan je od termodinamičkih procesa koji se javljaju pri indikatoru konstantnog tlaka. Masa plinskog sustava istovremeno ostaje konstantna. Vizualni prikaz grafa koji prikazuje izobarični proces daje se termodinamičkim dijagramom u odgovarajućem koordinatnom sustavu.

primjeri

Najjednostavniji primjer izobarnog procesa je zagrijavanje određenog volumena vode u otvorenoj posudi. Kao drugi primjer, može se dati ekspanzija idealnog plina u cilindričnom volumenu, gdje klip ima slobodan hod. U svakom od tih slučajeva tlak će biti konstantan. To je jednako običnom atmosferskom tlaku, što je sasvim očito.

preokretljivost

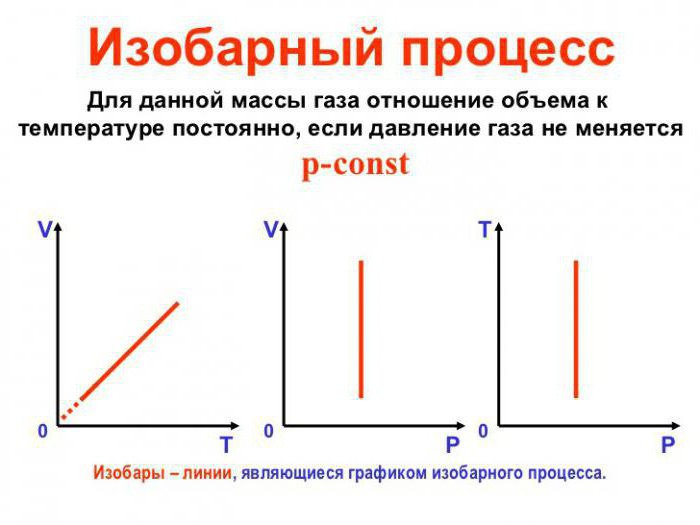
Izobarni se postupak može smatrati reverzibilnim ako se tlak u sustavu podudara s vanjskim tlakom i jednak je u svim točkama procesa (tj. Konstantan je u vrijednosti), a temperatura se vrlo sporo mijenja. Tako se termodinamička ravnoteža u sustavu održava u svakom trenutku vremena. Kombinacija gore navedenih faktora daje nam mogućnost da izobarni proces smatramo reverzibilnim.

Kako bi se u sustavu obavio izobarični proces, toplina se mora ili isporučiti ili ukloniti. U isto vrijeme, toplina se mora trošiti na rad na širenju idealnog plina i njegovu promjenu. unutarnja energija. Formula koja pokazuje ovisnost količina jednih na druge tijekom izobarnog procesa naziva se Gay-Lussacovim zakonom. To pokazuje da je volumen proporcionalan temperaturi. Izvedimo ovu formulu na temelju površnog znanja.

Zaključak Gay-Lussac Zakona (primarno razumijevanje)

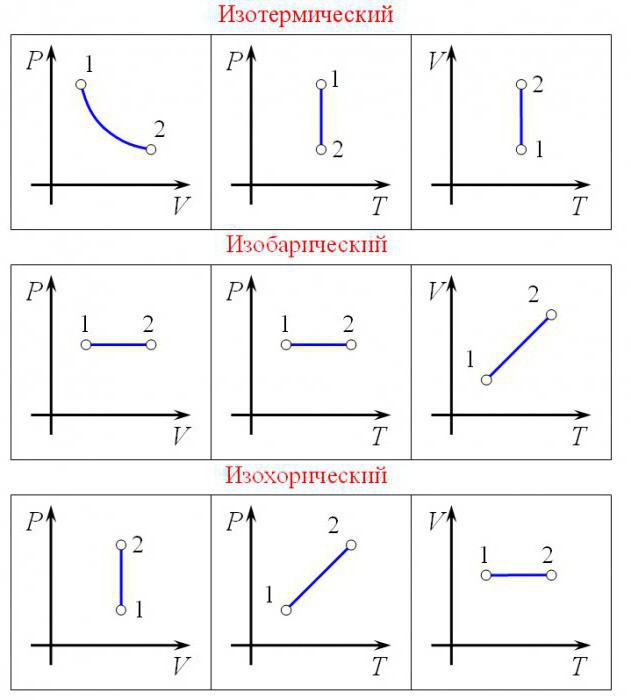
Čovjek, barem malo upućen u molekularnu fiziku, zna da su mnogi zadaci povezani s određenim parametrima. Njihovo ime je tlak plina, volumen plina i temperatura plina. U nekim slučajevima, molekularna i molarna masa količina tvari, univerzalna plinska konstanta i drugi pokazatelji. I postoji određena veza. Pričajmo detaljnije o univerzalnoj plinskoj konstanti. U slučaju da netko ne zna kako ga dobiti.

Dobivanje univerzalne plinske konstante

Ta konstanta (konstantni broj s određenom dimenzijom) također se naziva Mendeljejeva konstanta. Također je prisutan u Mendelejev-Clapeyron jednadžbi za idealan plin. Kako je naš poznati fizičar dobio ovu konstantu?

Kao što znamo, idealna jednadžba plina ima sljedeći oblik: PV / T (što je zvučalo ovako: "proizvod tlaka i volumena podijeljen s temperaturom"). S obzirom na univerzalnu plinsku konstantu, tzv Avogadrov zakon. Kaže se da, ako uzmemo bilo kakav plin, njegov jednak broj molova na istoj temperaturi i istom tlaku zauzima isti volumen.

Zapravo, riječ je o verbalnoj formulaciji jednadžbe stanja idealnog plina, koja je nešto ranije napisana u formuli formule. Ako uzmemo normalne uvjete (a to je kada je temperatura plina 273,15 Kelvina, tlak je 1 atmosfera, odnosno 101325 Paskala, a volumen mola plina 22,4 litre) i mi ih zamjenimo u jednadžbu, pomnožimo i podijelimo sve, a zatim dobijemo da nam kombinacija takvih postupaka daje brojčanu vrijednost jednaku 8,31. Dimenzija je prikazana u džulima, podijeljena proizvodom mola na Kelvin (j / mol * k).

Mendelejev-Clapeyronova jednadžba

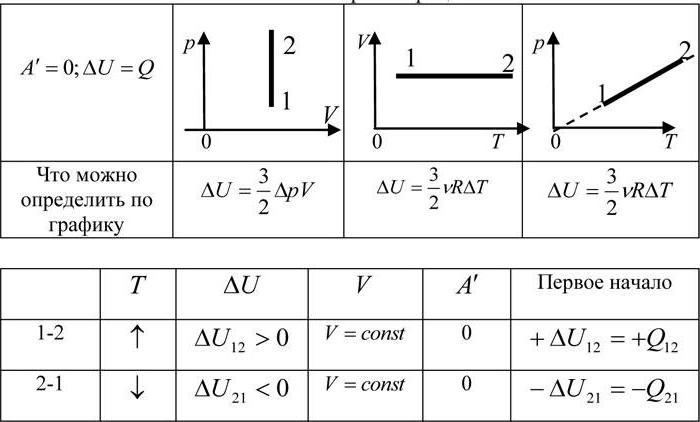
Uzmimo jednadžbu stanja idealnog plina i prepišemo ga u novom obliku. Prvobitna jednadžba, prisjećamo se, ima oblik PV / T = R. I sada pomnožimo oba dijela s indeksom temperature. Dobivamo formulu PV (m) = RT. To jest, proizvod tlaka po volumenu jednak je proizvodu univerzalne plinske konstante temperature.

Sada pomnožite obje strane jednadžbe s jednim ili drugim brojem molova. Njihov broj označavamo slovom, npr. X. Tako dobivamo sljedeću formulu: PV (m) X = XRT. Ali znamo da proizvod V s indeksom "m" rezultira samo volumenom V, a broj mola X se otkriva u obliku dijeljenja određene mase na molarnu masu, tj. Ona ima oblik m / M.

Stoga će konačna formula izgledati ovako: PV = MRT / m. To je upravo jednadžba Mendelejev-Clapeyrona, kojoj su oba fizičara stigla gotovo istodobno. Možemo pomnožiti desnu stranu jednadžbe (i istodobno podijeliti) s Avogadro broj. Tada dobivamo: PV = XN (a) RT / N (a). No, produkt broja molova Avogadrovim brojem, tj. XN (a), ne daje nam ništa više od ukupnog broja molekula plina, označenih slovom N.

Istovremeno, kvocijent univerzalne plinske konstante i Avogadrovog broja - R / N (a) dat će Boltzmannu konstantu (označenu s k). Kao rezultat toga, dobivamo drugu formulu, ali u nešto drugačijoj formi. Evo ga: PV = NkT. Ovu formulu možete otvoriti i dobiti sljedeći rezultat: NkT / V = ​​P.

Plinski rad u izobarnom procesu

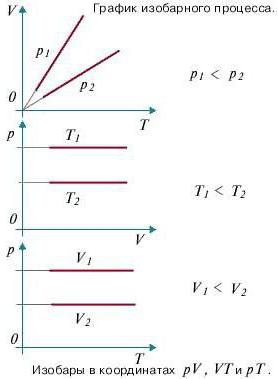
Kao što smo ranije otkrili, izobarni proces je termodinamički proces u kojem tlak ostaje konstantan. A kako bismo otkrili kako će se rad odrediti tijekom izobarnog procesa, morat ćemo se okrenuti prvom zakonu termodinamike. Opća formula je sljedeća: dQ = dU + dA, gdje je dQ količina topline, dU je promjena unutarnje energije, a dA je rad obavljen tijekom izvođenja termodinamičkog procesa.

Sada razmislite o izobarnom procesu. Uzmite u obzir faktor da tlak ostaje konstantan. Sada pokušajte prepisati prvi početak termodinamike za izobarični proces: dQ = dU + pdV. Da biste dobili vizualni prikaz procesa i rada, morate ga prikazati u koordinatnom sustavu. Neka je apscisa os, p, ordinatna os V. Neka se volumen poveća. Na dvije točke koje se međusobno razlikuju s odgovarajućom vrijednošću p (naravno, fiksne), zabilježite stanja koja predstavljaju V1 (početni volumen) i V2 (konačni volumen). U ovom slučaju, graf će biti ravna linija paralelna s osi x.

Pronalaženje posla lakše je nego ikad. To će jednostavno biti područje figure, omeđeno s obje strane projekcijama na os apscise, a na trećoj strani ravnu liniju koja povezuje točke koje se nalaze na početku i na kraju izobarične ravne linije. Pokušajmo izračunati vrijednost rada pomoću integrala.

Izračunat će se na sljedeći način: A = p (integral između V1 i V2) dV. Otvorimo integral. Dobivamo da će rad biti jednak proizvodu pritiska na razliku u volumenu. To jest, formula će izgledati ovako: A = p (V2 - V1). Ako otkrijemo neke količine, dobivamo drugu formulu. Izgleda ovako: A = xR (T2 - T2), gdje je x količina tvari.

Univerzalna plinska konstanta i njezino značenje

Može se reći da će posljednji izraz odrediti fizičko značenje R - univerzalne plinske konstante. Da bi to bilo jasnije, okrenimo se određenim brojevima. Uzmi za testiranje jedan mol tvari. U isto vrijeme neka temperatura bude 1 Kelvin. U ovom slučaju, lako je vidjeti da će rad plina biti jednak univerzalnoj plinskoj konstanti (ili obratno).

zaključak

Ta se činjenica može prikazati u malo drugačijem svjetlu, parafrazirajući tekst. Primjerice, univerzalna plinska konstanta brojčano će biti jednaka radu tijekom izobarnog ekspanzije s jednim molom idealnog plina ako se zagrijava za jedan Kelvin. Nešto će teže izračunati rad s drugim izoprocesima, ali glavno je primijeniti logiku. Onda će sve brzo pasti na svoje mjesto, a izvođenje formule će biti lakše nego što mislite.