Vjerojatnost događaja Određivanje vjerojatnosti događaja

U početku, kao zbirka informacija i empirijskih opažanja igre kockicama, teorija vjerojatnosti postala je čvrsta znanost. Prvi koji joj je dao matematički okvir bili su Farma i Pascal.

Od razmišljanja o vječnoj teoriji vjerojatnosti

Dvije osobnosti kojima teorija vjerojatnosti duguje mnoge temeljne formule, Blaise Pascal i Thomas Bayes, poznate su kao duboko religiozni ljudi, a drugi kao prezbiterijanski svećenik. Očigledno, želja tih dvaju znanstvenika da dokažu zabludu mišljenja o određenoj Fortune, dajući sreću svojim kućnim ljubimcima, dala je poticaj istraživanju u ovom području. Uostalom, svaka igra na sreću sa svojim dobitcima i gubicima samo je simfonija matematičkih načela.

Zahvaljujući uzbuđenju kavalira Meréa, koji je bio jednako igrač i osoba koja nije ravnodušna prema znanosti, Pascal je bio prisiljen pronaći način da izračuna vjerojatnost. De Mere je zanimalo takvo pitanje: "Koliko puta morate baciti dvije kockice u paru kako biste dobili 12 bodova više od 50%?" Drugo pitanje, iznimno zainteresirano za gospodina: "Kako podijeliti ulog između sudionika nedovršene igre?" Naravno, Pascal je uspješno odgovorio na oba pitanja de Merea, koji je postao nesvjestan pokretač razvoja teorije vjerojatnosti. Zanimljivo je da je persona de Mere ostala poznata na ovom području, a ne u literaturi.

Prije toga nijedan matematičar nije pokušao izračunati vjerojatnosti događaja, budući da se smatralo da je to samo odluka o proricanju sudbine. Blaise Pascal je dao prvu definiciju vjerojatnosti događaja i pokazao da je to specifična figura koja se može matematički potkrijepiti. Teorija vjerojatnosti postala je osnova za statistiku i široko se koristi u modernoj znanosti.

Što je nesreća

Ako uzmemo u obzir test koji se može ponoviti beskonačan broj puta, tada možemo definirati slučajni događaj. To je jedan od mogućih ishoda eksperimenta.

Iskustvo je provedba konkretnih akcija u nepromijenjenim uvjetima.

Za rad s rezultatima iskustva, događaji su obično označeni slovima A, B, C, D, E ...

Vjerojatnost slučajnog događaja

Da bismo prešli na matematički dio vjerojatnosti, potrebno je definirati sve njegove komponente.

Vjerojatnost događaja je numerički izražena mjera mogućnosti nastanka određenog događaja (A ili B) kao rezultat iskustva. Označava vjerojatnost kao P (A) ili P (B).

U teoriji vjerojatnosti, razlikuje se:

• zajamčeno je da će se pouzdani događaj pojaviti kao rezultat eksperimenta P (=) = 1;
• nemoguće da se događaj nikada ne može dogoditi P (Ø) = 0;
• slučajni događaj leži između pouzdanog i nemogućog, tj. vjerojatnost njegovog pojavljivanja je moguća, ali nije zajamčena (vjerojatnost slučajnog događaja je uvijek unutar 0≤P (A) ≤ 1).

Odnos između događaja

Razmotrimo i jedan i zbroj događaja A + B, kada događaj broji u implementaciji barem jedne od komponenti, A ili B, ili oboje - A i B.

U odnosu jedni na druge, događaji mogu biti:

• Jednako.
• Kompatibilni.
• Nespojivo.
• Suprotno (međusobno se isključuju).
• Ovisni.

Ako se dva događaja mogu pojaviti s jednakom vjerojatnošću, onda su jednako moguća .

Ako pojava događaja A ne poništava vjerojatnost pojave događaja B, onda su oni kompatibilni.

Ako se događaji A i B nikada ne pojavljuju istovremeno u istom iskustvu, nazivaju se nekompatibilni . Dobar je primjer bacanje novčića: izgled repa je automatski ne-pojavljivanje orla.

Vjerojatnost zbira takvih nekompatibilnih događaja sastoji se od zbroja vjerojatnosti svakog događaja:

R (A + V) = R (A) + R (V)

Ako pojava jednog događaja onemogućuje da se drugi dogodi, onda se nazivaju suprotnim. Tada je jedan od njih označen kao A, a drugi - Ā (čitaj se kao "ne A"). Pojava događaja A znači da nije došlo do. Ova dva događaja čine potpunu skupinu s zbrojem vjerojatnosti jednakim 1.

Zavisni događaji imaju uzajamni utjecaj, smanjujući ili povećavajući međusobnu vjerojatnost.

Odnos između događaja. primjeri

Primjerima je mnogo lakše razumjeti principe teorije vjerojatnosti i kombinaciju događaja.

Iskustvo koje će se provesti jest izvući lopte iz kutije, a rezultat svakog iskustva je elementarni ishod.

Događaj je jedan od mogućih ishoda iskustva - crvena lopta, plava kugla, lopta sa brojem šest i tako dalje.

Broj testa 1. Uključeno je 6 lopti, od kojih su tri plave boje, na njih se primjenjuju neparni brojevi, a ostala tri su crvena s parnim brojevima.

Test broj 2. Postoji 6 plavih kugli s brojevima od jedan do šest.

Na temelju ovog primjera možete nazvati kombinacije:

• Pouzdan događaj. Na španjolskom Događaj 2 “dobiti plavu kuglu” je pouzdan, jer je vjerojatnost njegovog pojavljivanja 1, budući da su sve lopte plave i ne može biti promašaja. Dok događaj "dobiti loptu s brojem 1" - slučajni.
• Nemogući događaj. Na španjolskom №1 s plavim i crvenim lopticama događaj "dobiti ljubičasta lopta" je nemoguće, jer je vjerojatnost njegova pojava je 0.
• Jednaki događaji. Na španjolskom Događaji broj 1 „dobivaju loptu s brojem 2“ i „dobivanje lopte s brojem 3“ jednako su mogući, a događaji „dobivanje lopte s parnim brojem“ i „dobivanje lopte s brojem 2“ imaju različitu vjerojatnost.
• Kompatibilni događaji. Dva puta za redom da bi dobili šest u procesu bacanja umrijeti - to su kompatibilni događaji.
• Nekompatibilni događaji. U istom isp. No1 događaji "dobiti crvenu loptu" i "dobiti loptu s neparnim brojem" ne mogu se kombinirati u istom iskustvu.
• Suprotni događaji. Najživlji primjer ovoga je bacanje kovanica, kada je vučenje orla jednako nevučenju repova, a zbroj njihovih vjerojatnosti je uvijek 1 (puna skupina).
• Ovisni događaji . Dakle, na španjolskom. Br. 1 može se podesiti da dvaput zaredom izvadi crvenu kuglu. Njegova ekstrakcija ili ne ekstrakcija po prvi put utječe na vjerojatnost ekstrakcije po drugi put.

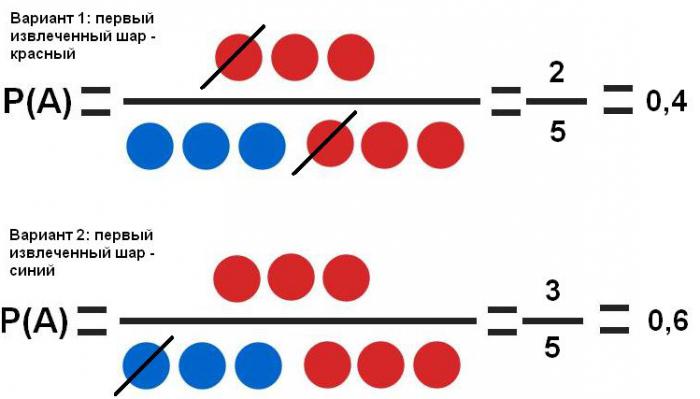
Vidljivo je da prvi događaj značajno utječe na vjerojatnost drugog (40% i 60%).

Formula vjerojatnosti događaja

Prijelaz iz refleksije proricanja sudbine na točne podatke događa se prenošenjem teme na matematičku ravninu. To jest, prosudbe o slučajnom događaju kao što su "velika vjerojatnost" ili "minimalna vjerojatnost" mogu se prevesti u konkretne numeričke podatke. Takav materijal je već dopušten za procjenu, usporedbu i ulazak u složenije izračune.

S točke gledišta izračuna, određivanje vjerojatnosti događaja je omjer broja elementarnih pozitivnih ishoda i broja mogućih ishoda iskustva u odnosu na određeni događaj. Vjerojatnost je označena s P (A), gdje P znači riječ "probabilit", što se s francuskog prevodi kao "vjerojatnost".

Dakle, formula vjerojatnosti događaja:

P (A) = m / n,

Gdje je m broj povoljnih ishoda za događaj A, n je zbroj svih mogućih ishoda za ovo iskustvo. U ovom slučaju, vjerojatnost događaja uvijek leži između 0 i 1:

0 ≤ P (A) ≤ 1.

Izračunavanje vjerojatnosti događaja. primjer

Uzmi sp. Br. 1 s kuglicama, kao što je opisano ranije: 3 plave lopte s brojevima 1/3/5 i 3 crvene s brojevima 2/4/6.

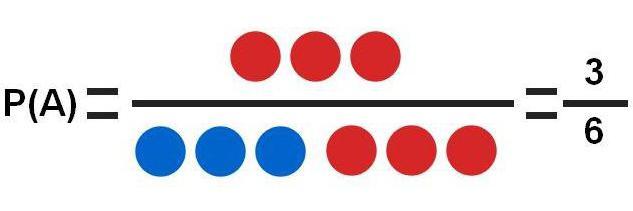
Na temelju ovog testa može se razmotriti nekoliko različitih zadataka:

• A - gubitak crvene kugle. Postoje 3 crvene loptice, a ukupno ima 6 opcija.To je najjednostavniji primjer u kojem je vjerojatnost događaja P (A) = 3/6 = 0.5.
• B - gubitak parnog broja. Ukupan broj parnih brojeva je 3 (2,4,6), a ukupan broj mogućih numeričkih varijanti je 6. Vjerojatnost tog događaja je P (B) = 3/6 = 0.5.
• C - gubitak broja većeg od 2. Ukupno postoje 4 takve opcije (3,4,5,6) od ukupnog broja mogućih ishoda 6. Vjerojatnost događaja C jednaka je P (C) = 4/6 = 0,67.

Kao što se može vidjeti iz izračuna, događaj C ima veću vjerojatnost, budući da je broj vjerojatno pozitivnih ishoda veći nego u A i B.

Događaji koji nisu u skladu

Takvi se događaji ne mogu istodobno pojaviti u istom iskustvu. Kao na španjolskom No. 1 nemoguće je istovremeno dobiti plavu i crvenu loptu. To jest, možete dobiti ili plavu ili crvenu kuglu. Slično tome, u kocki se čak ni ne može pojaviti u isto vrijeme. neparan broj.

Vjerojatnost dvaju događaja smatra se vjerojatnošću njihovog zbroja ili proizvoda. Zbroj takvih događaja A + B smatra se takvim događajem, koji se sastoji u pojavljivanju događaja A ili B, a proizvod njihovog AB - u izgledu oboje. Na primjer, pojavljivanje dvije šestice odjednom na licima dviju kockica u jednom valjku.

Zbroj nekoliko događaja je događaj koji uključuje pojavu barem jednog od njih. Stvaranje nekoliko događaja je zajednički nastup svih njih.

U teoriji vjerojatnosti, u pravilu, uporaba sindikata "i" označava zbroj, uniju "ili" - množenje. Formule s primjerima pomoći će razumjeti logiku zbrajanja i množenja u teoriji vjerojatnosti.

Vjerojatnost zbroja nekonzistentnih događaja

Ako se razmatra vjerojatnost nekompatibilnih događaja, tada je vjerojatnost zbira događaja jednaka zbrajanju njihovih vjerojatnosti:

R (A + V) = R (A) + R (V)

Na primjer: izračunajte vjerojatnost da u sp. №1 s plavim i crvenim kuglicama će ispasti broj između 1 i 4. Ne računamo u jednu radnju, već u zbroj vjerojatnosti elementarnih komponenti. Dakle, u ovom iskustvu, samo 6 lopti ili 6 svih mogućih ishoda. Brojevi koji zadovoljavaju uvjet su 2 i 3. Vjerojatnost odustajanja 2 je 1/6, vjerojatnost 3 je također 1/6. Vjerojatnost da je broj između 1 i 4 ispao jednak je:

1/6 + 1/6 = 1/3

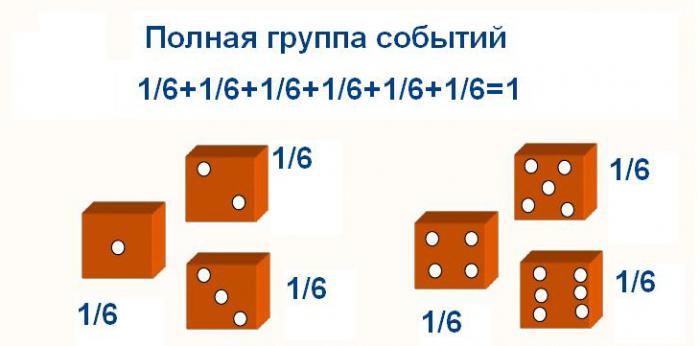
Vjerojatnost zbroja nespojivih događaja cijele skupine je 1.

Dakle, ako u eksperimentu s kockom zbrojimo vjerojatnosti ispuštanja svih znamenki, kao rezultat toga dobijemo jednu.

To vrijedi i za suprotne događaje, na primjer u iskustvu s novčićem, gdje je jedna strana događaj A, a drugi je suprotan događaj Ā, kao što je dobro poznato.

R (A) + R (Ā) = 1

Vjerojatnost stvaranja nekompatibilnih događaja

Množenje vjerojatnosti koristi se pri razmatranju pojave dva ili više nekompatibilnih događaja u jednom promatranju. Vjerojatnost da se događaji A i B pojavljuju istovremeno u njoj jednaka je proizvodu njihovih vjerojatnosti, ili:

R (A * V) = R (A) * R (V)

Na primjer, vjerojatnost da u sp. # 1 kao rezultat dva pokušaja dvaput pojavit će se plava kugla, jednaka

½ * ½ = ¼

To jest, vjerojatnost događaja, kada će se kao rezultat dva pokušaja izvlačenja loptica samo plavih loptica izvaditi, iznosi 25%. Vrlo je lako napraviti praktične pokuse ovog zadatka i vidjeti je li to doista slučaj.

Zajednička događanja

Događaji se smatraju zajedničkim kada se pojava jednog od njih može podudarati s pojavom drugog. Unatoč činjenici da su zajedničke, razmatra se vjerojatnost neovisnih događaja. Na primjer, bacanje dviju kockica može dati rezultat kada se na njih oboje pojavi broj 6. Iako su se događaji podudarali i pojavljivali u isto vrijeme, oni su neovisni jedni od drugih - moglo bi pasti samo jedan šest, druga kost ne bi imala utjecaj.

Vjerojatnost zajedničkih događaja smatra se vjerojatnošću njihovog zbira.

Vjerojatnost zbroja zajedničkih događaja. primjer

Vjerojatnost zbira događaja A i B, koji su međusobno povezani, jednaka je zbroju vjerojatnosti događaja minus vjerojatnost njihova rada (tj. Njihova zajednička provedba):

R _spoja. (A + B) = P (A) + P (B) - P (AB)

Pretpostavimo da je vjerojatnost udarca u metu s jednim metkom 0,4. Zatim događaj A - udaranje u cilj u prvom pokušaju, B - u drugom. Ovi događaji su zajednički, jer je moguće da možete pogoditi metu iz prvog i drugog udarca. Ali događaji nisu ovisni. Kolika je vjerojatnost pojave događaja poraziti metu s dva udarca (barem jedan)? Prema formuli:

0,4 + 0,4-0,4 x 0,4 = 0,64

Odgovor na pitanje glasi: "Vjerojatnost da pogodimo metu s dva hica je 64%."

Ova formula za vjerojatnost događaja može se primijeniti i na nespojive događaje, gdje je vjerojatnost zajedničkog pojavljivanja događaja P (AB) = 0. To znači da se vjerojatnost zbira nekompatibilnih događaja može smatrati posebnim slučajem predložene formule.

Geometrija vjerojatnosti za jasnoću

Zanimljivo je da se vjerojatnost zbira zajedničkih događaja može predstaviti u obliku dvije regije A i B, koje se međusobno sijeku. Kao što se može vidjeti na slici, područje njihove povezanosti jednako je ukupnoj površini minus područje njihova raskrižja. Ovo geometrijsko objašnjenje čini da je formula nelogična na prvi pogled razumljivija. Imajte na umu da geometrijska rješenja nisu neuobičajena u teoriji vjerojatnosti.

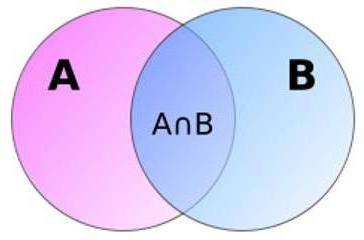
Utvrđivanje vjerojatnosti zbira skupa (više od dvije) zajedničkih događaja prilično je glomazno. Da biste je izračunali, morate upotrijebiti formule koje su navedene za te slučajeve.

Ovisni događaji

Zavisni događaji nazivaju se ako pojava jednog (A) od njih utječe na vjerojatnost pojavljivanja drugog (B). Štoviše, uzima se u obzir i utjecaj pojavljivanja događaja A i njegovog ne pojavljivanja. Iako se događaji nazivaju ovisni po definiciji, samo jedan od njih ovisi (B). Uobičajena vjerojatnost označena je kao P (B) ili vjerojatnost neovisnih događaja. U slučaju uzdržavanih osoba uveden je novi koncept - uvjetna vjerojatnost P _A (B), koja je vjerojatnost ovisnog događaja B pod uvjetom da se dogodi događaj A (hipoteza), o čemu ovisi.

No, događaj A je također slučajan, stoga također ima vjerojatnost koja se mora i može uzeti u obzir u proračunima. Sljedeći će primjer pokazati kako raditi s ovisnim događajima i hipotezom.

Primjer izračuna vjerojatnosti ovisnih događaja

Dobar primjer za izračunavanje ovisnih događaja može biti standardna špila karata.

Koristeći primjer palube od 36 kartica, razmatramo ovisne događaje. Potrebno je odrediti vjerojatnost da će druga kartica, izvađena s palube, biti od dijamantnog odijela, ako je prva karta:

1. Dijamanti
2. Još jedno odijelo.

Očigledno je da vjerojatnost drugog događaja B ovisi o prvom A. Dakle, ako je prva opcija valjana, da je na palubi bila 1 karta (35) i 1 dijamant (8) manje, vjerojatnost događaja B:

PA (B) = 8/35 = 0,23

Ako je druga opcija valjana, onda je na palubi 35 karata, a još uvijek je sačuvan cijeli broj tamburina (9), zatim vjerojatnost sljedećeg događaja B:

_{R A} (V) = 9/35 = 0,26.

Može se vidjeti da ako je događaj A uvjetovan činjenicom da je prva kartica tamburina, tada se vjerojatnost događaja B smanjuje i obrnuto.

Množenje ovisnih događaja

Vođeni prethodnim poglavljem, prihvaćamo prvi događaj (A) kao činjenicu, ali ako govorimo u biti, to je slučajno. Vjerojatnost ovog događaja, odnosno vađenje dijamanata iz špila karata, jednaka je:

P (A) = 9/36 = 1/4

Budući da teorija ne postoji sama od sebe, već je namijenjena za praktične svrhe, pošteno je napomenuti da je vjerojatnost proizvodnje ovisnih događaja najčešće potrebna.

Prema teoremu o proizvodu vjerojatnosti ovisnih događaja, vjerojatnost pojavljivanja zajednički ovisnih događaja A i B jednaka je vjerojatnosti jednog događaja A pomnoženog s uvjetnom vjerojatnošću događaja B (ovisno o A):

P (AB) = P (A) * P _A (B)

Zatim, u primjeru s palubom, vjerojatnost vađenja dviju kartica s odijelom dijamanata je:

9/36 * 8/35 = 0.0571, ili 5.7%

A vjerojatnost vađenja u početku nije tamburaša, a zatim tamburin je jednak:

27/36 * 9/35 = 0,19, ili 19%

Može se vidjeti da je vjerojatnost pojave događaja B veća, pod uvjetom da se prvo izdvoji kartica odijela, različita od dijamanta. Ovaj rezultat je sasvim logičan i razumljiv.

Ukupna vjerojatnost događaja

Kada problem s uvjetnim vjerojatnostima postane višestruk, ne može se izračunati konvencionalnim metodama. Kada postoji više od dvije hipoteze, tj. A1, A2, ..., A _n , .. čini kompletnu skupinu događaja, pod uvjetom:

• P (A _i )> 0, i = 1,2, ...
• A _{i j} A _j = Ø, i ≠ j.
• Σk A _k = Ω.

Dakle, formula ukupne vjerojatnosti za događaj B s punom skupinom slučajnih događaja A1, A2, ..., A _n jednaka je _:

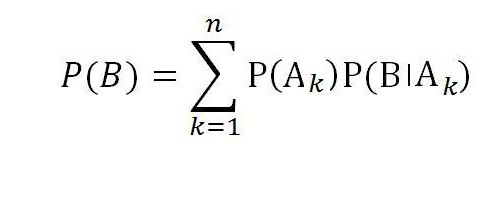
Gledajući u budućnost

Vjerojatnost slučajnog događaja bitna je u mnogim područjima znanosti: ekonometriji, statistici, fizici, itd. Budući da se neki procesi ne mogu odrediti deterministički, budući da su oni sami po sebi vjerojatnosni, potrebne su posebne metode rada. Teorija vjerojatnosti događaja može se koristiti u bilo kojem tehnološkom području kao način utvrđivanja mogućnosti pogreške ili kvara.

Možemo reći da, prepoznajući vjerojatnost, na neki način provodimo teoretski korak u budućnost, ispitujući ga kroz prizmu formula.