Kvadratne jednadžbe. Rješavanje jednadžbi kvadrata
Isprva se ova tema može činiti kompliciranom zbog mnogih ne baš jednostavnih formula. Ne samo da kvadratne jednadžbe imaju duge unose, nego se i korijeni mogu naći i preko diskriminanta. Postoji ukupno tri nove formule. Nije lako zapamtiti. To je moguće tek nakon čestog rješavanja takvih jednadžbi. Tada će se sve formule pamtiti same.

Opći prikaz kvadratne jednadžbe
Ovdje im se nudi eksplicitan zapis, kada se najprije zabilježi najveći stupanj, a zatim - silaznim redoslijedom. Često postoje situacije u kojima su komponente međusobno suprotne. Tada je bolje izmijeniti jednadžbu u opadajućem redoslijedu stupnja varijable.
Predstavljamo zapis. Prikazani su u tablici u nastavku.
| Oznaka veličine | Njeno ime |
| a, b, c | koeficijenti koji su proizvoljni brojevi |
| x | varijabla |
| D | diskriminacijska |
| x 1 x 2 | korijeni jednadžbe |
Ako prihvatimo ove oznake, sve kvadratne jednadžbe svodimo se na sljedeći unos.
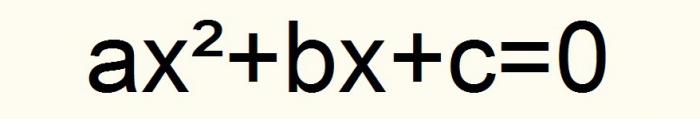
Štoviše, koeficijent a Let 0. Neka ova formula bude označena brojem jedan.
Kada je jednadžba dana, nejasno je koliko će korijena biti u odgovoru. Zato što je jedna od tri opcije uvijek moguća:
- otopina će imati dva korijena;
- odgovor je jedan broj;
- korijeni jednadžbe uopće neće biti.
I dok odluka nije dovršena, teško je razumjeti koja od opcija će pasti u određenom slučaju.
Vrste zapisa kvadratnih jednadžbi
U zadacima mogu postojati različiti unosi. Neće uvijek izgledati kao opća formula za kvadratnu jednadžbu. Ponekad će propustiti neke od stavki. Ono što je gore napisano je potpuna jednadžba. Ako uklonite drugi ili treći pojam u njemu, dobijete nešto drugo. Ti se zapisi nazivaju i kvadratne jednadžbe, samo nepotpune.
Štoviše, samo pojmovi čiji su koeficijenti "u" i "c" mogu nestati. Broj "a" ne može biti nula ni pod kojim uvjetima. Budući da se u ovom slučaju formula pretvara u linearnu jednadžbu. Formule za nepotpuni oblik jednadžbi su sljedeće:
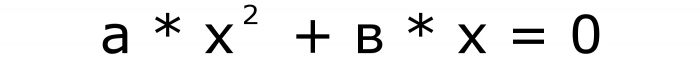
i
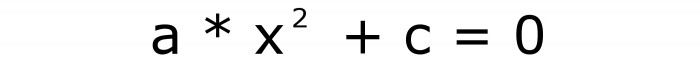
Dakle, postoje samo dvije vrste, osim pune, postoje i nepotpune kvadratne jednadžbe. Neka prva formula bude broj dva, a druga tri.
Diskriminantan i ovisnost broja korijena o njegovoj vrijednosti
Morate znati taj broj kako biste izračunali korijeni jednadžbe. Uvijek se može izračunati, bez obzira na formulu kvadratne jednadžbe. Da biste izračunali diskriminantnu osobu, morate upotrijebiti donju jednadžbu koja će imati broj četiri.

Nakon zamjene vrijednosti koeficijenata u ovoj formuli, možete dobiti brojeve s različitim znakovima. Ako je odgovor da, onda će odgovor na jednadžbu biti dva različita korijena. S negativnim brojem, korijeni kvadratne jednadžbe neće biti prisutni. U slučaju jednakosti nuli, odgovor će biti jedan.
Kako se rješava kvadratna jednadžba cjelovitog obrasca?
Zapravo, razmatranje ovog pitanja već je počelo. Jer prvo morate pronaći diskriminanta. Kad je jasno da postoje korijeni kvadratne jednadžbe, a njihov broj je poznat, potrebno je koristiti formule za varijable. Ako postoje dva korijena, tada morate primijeniti ovu formulu.
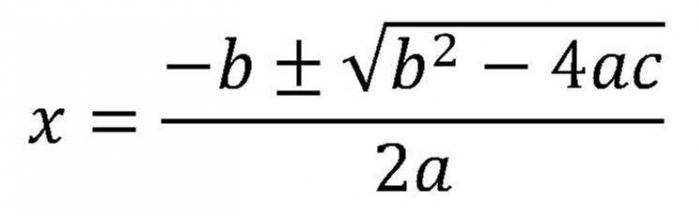
Budući da u njemu postoji znak "±", postojat će dvije vrijednosti. Izraz kvadratnog korijena je diskriminantan. Stoga se formula može ponovno napisati drugačije.
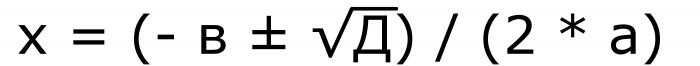
Formula 5. Iz istog zapisa jasno je da ako je diskriminant nula, tada će oba korijena uzeti iste vrijednosti.
Ako rješenje kvadratnih jednadžbi još nije razrađeno, bolje je zapisati vrijednosti svih koeficijenata prije primjene diskriminantnih i varijabilnih formula. Kasnije ovaj trenutak neće uzrokovati poteškoće. Ali na samom početku dolazi do zbrke.
Kako se rješava kvadratna nepotpuna jednadžba?
Ovdje je sve mnogo jednostavnije. Čak i nema potrebe za dodatnim formulama. I ne trebaju oni koji su već zabilježeni za diskriminanta i nepoznato.
Najprije ćemo razmotriti nepotpunu jednadžbu broj dva. U toj jednakosti pretpostavlja se da se nepoznata vrijednost stavi iz zagrade i riješi linearna jednadžba koja će ostati u zagradama. Odgovor će biti dva korijena. Prvi je nužno jednak nuli, jer postoji faktor koji se sastoji od same varijable. Drugi će se pojaviti na odluci linearna jednadžba.
Nepotpuna jednadžba broj tri rješava se prijenosom broja s lijeve strane jednakosti u desno. Tada morate podijeliti s koeficijentom prema nepoznatom. Ostaje samo izdvajanje kvadratni korijen i zapamtite da je zapišete dva puta s suprotnim znakovima.

Korisni savjeti
Zatim zapisujemo neke radnje koje nam pomažu naučiti kako riješiti sve vrste jednakosti koje se pretvaraju u kvadratne jednadžbe. Oni će pomoći učeniku da izbjegne nepažnje. Ti su nedostaci uzrok slabih procjena u proučavanju opsežne teme "Kvadratne jednadžbe (razred 8)". Nakon toga, ove akcije neće morati stalno izvesti. Zato što će postojati stalna vještina.
- Prvo trebate napisati jednadžbu u standardnom obliku. To jest, najprije izraz s najvećim stupnjem varijable, a zatim - bez stupnja i posljednjeg - samo broj.
- Ako se ispred koeficijenta "a" pojavi minus, tada može zakomplicirati posao početniku za proučavanje kvadratnih jednadžbi. Bolje ga je riješiti. U tu svrhu, sva jednakost mora biti pomnožena sa "-1". To znači da će svi izrazi promijeniti znak u suprotno.
- Na isti se način preporučuje da se riješite frakcija. Jednostavno pomnožite jednadžbu s odgovarajućim množiteljem, tako da su denominatori smanjeni.

primjeri
Potrebne su sljedeće kvadratne jednadžbe:
x2 - 7x = 0;
5x2 - 30 = 0;
15 - 2x - x2 = 0;
x2 + 8 + 3x = 0;
12x + x2 + 36 = 0;
(x + 1) 2 + x + 1 = (x + 1) (x + 2).
Prva jednadžba: x2 - 7x = 0. Ona je nepotpuna, stoga je riješena kao što je opisano za formulu dva.
Nakon stavljanja zagrada, x (x - 7) = 0.
Prvi korijen uzima vrijednost: x 1 = 0. Drugi će se naći iz linearne jednadžbe: x - 7 = 0. Lako je uočiti da je x 2 = 7.
Druga jednadžba: 5x 2 + 30 = 0. Opet nepotpuna. To se rješava samo kako je opisano za treću formulu.
Nakon prijenosa 30 na desnu stranu jednadžbe: 5x 2 = 30. Sada trebate podijeliti s 5. Ispada: x 2 = 6. Odgovori će biti brojevi: x 1 = ,6, x 2 = - .6.
Treća jednadžba: 15 - 2x - x 2 = 0. U daljnjem tekstu rješenje kvadratnih jednadžbi započinje ponovnim ispisivanjem u standardni oblik: - x 2 - 2x + 15 = 0. Sada je vrijeme da upotrijebimo drugi koristan savjet i sve pomnožimo sa minus jedan , Ispada da je x 2 + 2x - 15 = 0. Prema četvrtoj formuli, diskriminant se mora izračunati: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. To je pozitivan broj. Iz gore navedenog, ispada da jednadžba ima dva korijena. Potrebno ih je izračunati po petoj formuli. To znači da je x = (-2 ± )64) / 2 = (-2 ± 8) / 2. Tada x 1 = 3, x 2 = - 5.
Četvrta jednadžba x 2 + 8 + 3x = 0 pretvara se u ovo: x 2 + 3x + 8 = 0. Njegova diskriminanta jednaka je toj vrijednosti: -23. Budući da je ovaj broj negativan, odgovor na ovaj zadatak bit će sljedeći unos: "Nema korijena".
Petu jednadžbu 12x + x2 + 36 = 0 treba ponovno napisati na sljedeći način: x 2 + 12x + 36 = 0. Nakon primjene formule za diskriminant, dobivamo broj nula. To znači da će imati jedan korijen, to jest: x = -12 / (2 * 1) = -6.
Šesta jednadžba (x + 1) 2 + x + 1 = (x + 1) (x + 2) zahtijeva transformacije, koje se sastoje u dovođenju tih pojmova na mjesto prije otvaranja zagrada. Na mjestu prvog pojavit će se sljedeći izraz: x 2 + 2x + 1. Nakon jednakosti pojavit će se ovaj zapis: x 2 + 3x + 2. Nakon što se takvi pojmovi broje, jednadžba će izgledati kao: x 2 - x = 0. Pretvorila se u nepotpuna , Sličan njemu se već smatrao malo višim. Korijeni ovoga bit će brojevi 0 i 1.