Znakovi, sastavni elementi i svojstva jednakokračnog trokuta

Prvi povjesničari naše civilizacije - stari Grci - spominju Egipat kao rodno mjesto geometrije. Teško je s njima se ne slagati, znajući s kakvom je ogromnom preciznošću podignute divovske grobnice faraona. Međusobno raspoređivanje piramidalnih ravnina, njihovi razmjeri, orijentacija duž kardinalnih točaka - bilo bi nezamislivo postići takvo savršenstvo bez poznavanja osnova geometrije.

Riječ "geometrija" može se prevesti kao "dimenzija Zemlje". A riječ "zemlja" ne pojavljuje se kao planet - dio Sunčevog sustava, već kao avion. Označavanje područja za poljoprivredu najvjerojatnije je početna osnova znanosti o geometrijskim oblicima, njihovim vrstama i svojstvima.

Trokut je najjednostavnija prostorna figura planimetrije, koja sadrži samo tri točke - vrhove (ne može biti ni manje). Osnova temelja može biti zašto se u njemu pojavi nešto tajnovito i drevno. Svevideće oko unutar trokuta jedno je od najranijih poznatih okultnih znakova, a geografija njezine distribucije i vremenskog okvira jednostavno su nevjerojatni. Od drevnih egipatskih, sumerskih, Azteckih i drugih civilizacija do modernijih zajednica ljubitelja okultizma, raspršenih širom svijeta.

Što su trokuti

Pravilan svestrani trokut je zatvorena geometrijska figura koja se sastoji od tri segmenta različite duljine i tri kuta, od kojih nijedan nije u pravu. Osim toga, postoji nekoliko posebnih tipova.

Akutni trokut ima sve kutove manje od 90 stupnjeva. Drugim riječima - svi kutovi takvog trokuta su oštri.

Pravokutni trokut nad kojima su učenici cijelo vrijeme plakali zbog obilja teorema, ima jedan kut s magnitudom od 90 stupnjeva ili, kako se još naziva, ravnom linijom.

Tupi trokut odlikuje se činjenicom da je jedan od njegovih uglova tup, tj. Njegova je magnituda veća od 90 stupnjeva.

Istostranični trokut ima tri strane iste duljine. Takva figura također ima sve kutove.

Konačno, u jednakokračnom trokutu s tri strane, dva su jednaka.

Posebne značajke

Svojstva jednakostraničnog trokuta također određuju njegovu glavnu, glavnu, razliku - jednakost dviju strana. Te su se strane jednake jedna drugoj nazivaju bedrima (ili češće bočnim stranama), ali se treća strana naziva "temelj".

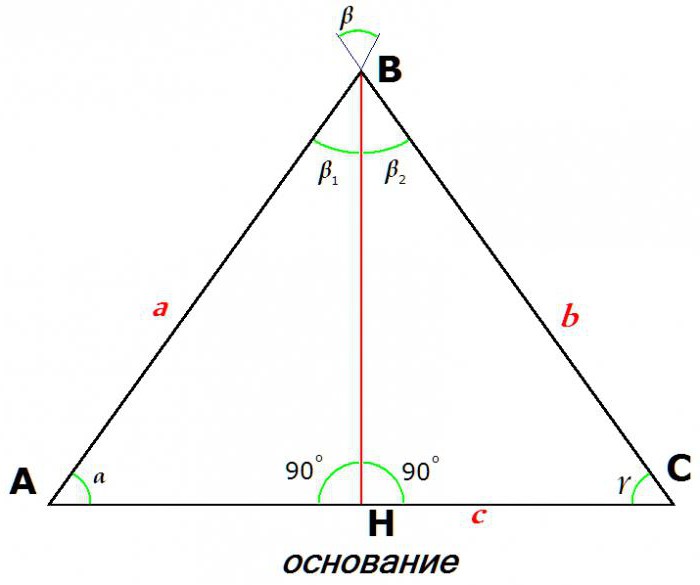
Na ovoj slici, a = b.

Drugi znak jednakokračnog trokuta slijedi iz sinusnog teorema. Budući da su stranice a i b jednake, sinusi njihovih suprotnih kutova su jednaki:

a / sin γ = b / sin α, odakle imamo: sin γ = sin α.

Jednakost sinusa podrazumijeva jednakost kutova: γ = α.

Dakle, drugi znak jednakokračnog trokuta je jednakost dvaju kutova susjednih baze.

Treći znak. Trokut razlikuje elemente kao što su visina, simetrala i medijana.

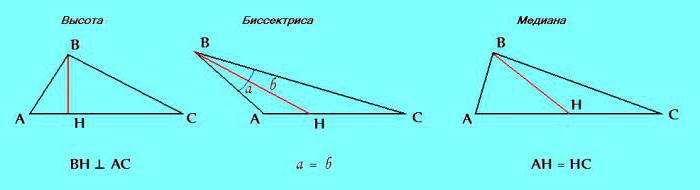
Ako se u procesu rješavanja problema ispostavi da su u razmatranom trokutu dva od tih elemenata isti: visina s simetrala; središnjica s medijan; srednja s visinom - definitivno je moguće zaključiti da je trokut jednakostraničan.

Geometrijska svojstva slike

1. Svojstva jednakostraničnog trokuta. Jedna od razlikovnih osobina figure je jednakost kutova susjednih baza:

α = γ;

<YOU = <BCA.

2. Drugo svojstvo o kojemu smo već govorili: medijan, simetrala i visina u jednakokračnom trokutu podudaraju se ako su građeni od njegovog vrha do baze.

3. Jednakost simetrala izvučenih iz vrhova baze:

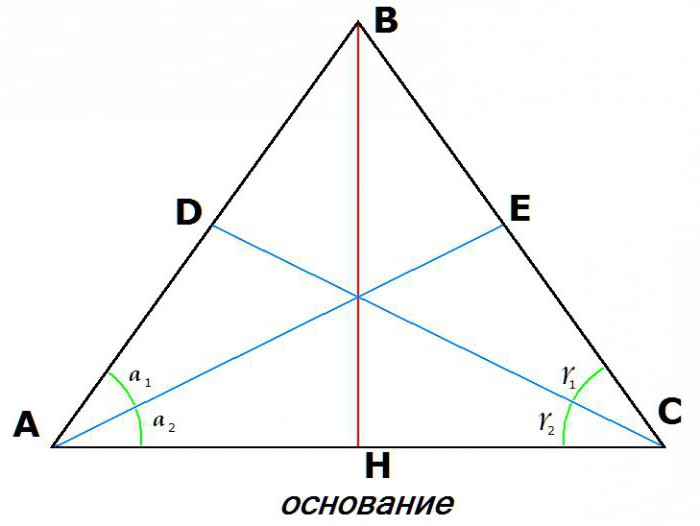
Ako je AE simetrala kuta YOU, a CD je simetrala kuta BCA, tada: AE = DC.

4. Svojstva jednakokračnog trokuta također osiguravaju jednakost visina, koje se izvlače iz vrhova u bazi.

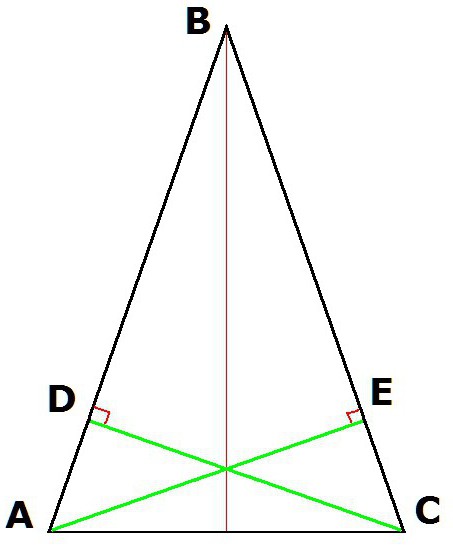
Ako iz vrhova A i C konstruiramo visine trokuta ABC (gdje je AB = BC), tada će nastali segmenti CD i AE biti jednaki.

5. Medijane izvučene iz uglova u bazi također će biti jednake.

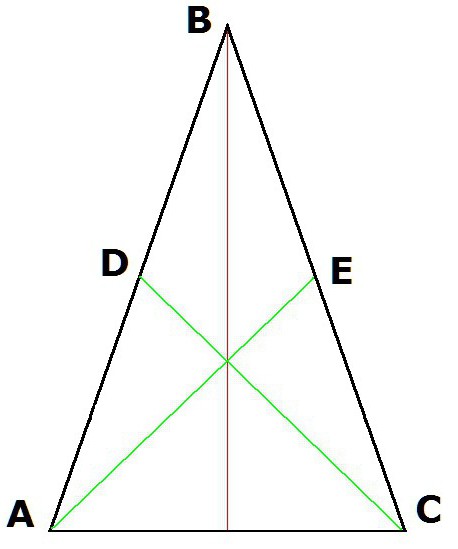
Dakle, ako su AE i DC medijan, to jest, AD = DB, i BE = EC, onda AE = DC.

Visina jednakokračnog trokuta

Jednakost strana i kutova na njima dodaje neke osobitosti izračunu duljine elemenata razmatrane figure.

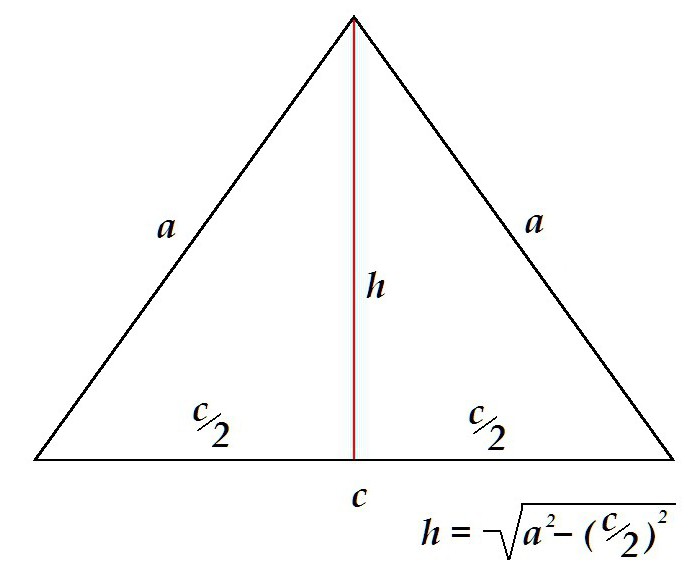
Visina u jednakokračnom trokutu dijeli lik na 2 simetrična pravokutna trokuta s hipotenusima u kojima se projektiraju strane. Visina u ovom slučaju određena je Pitagorinim teoremom kao noga.

Trougao može imati sve tri strane jednake, onda će se zvati jednakostraničan. Visina u jednakostraničnom trokutu određena je na isti način, samo za izračune dovoljno je znati samo jednu vrijednost - duljinu stranice ovog trokuta.

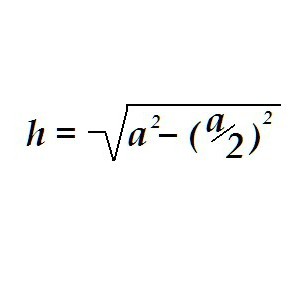
Visinu je moguće odrediti na drugi način, na primjer, poznavanje baze i ugla uz njega.

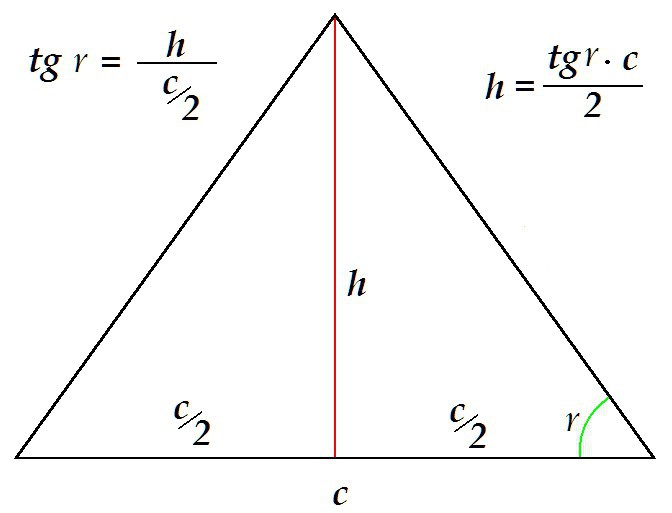
Medijan jednakostraničnog trokuta

Razmatrani tip trokuta, zbog svojih geometrijskih značajki, rješava se jednostavno jednostavnim minimalnim skupom izvornih podataka. Budući da je medijan u jednakokračnom trokutu jednak visini i bisektriksi, algoritam za određivanje ne razlikuje se od redoslijeda u kojem su ti elementi izračunati.

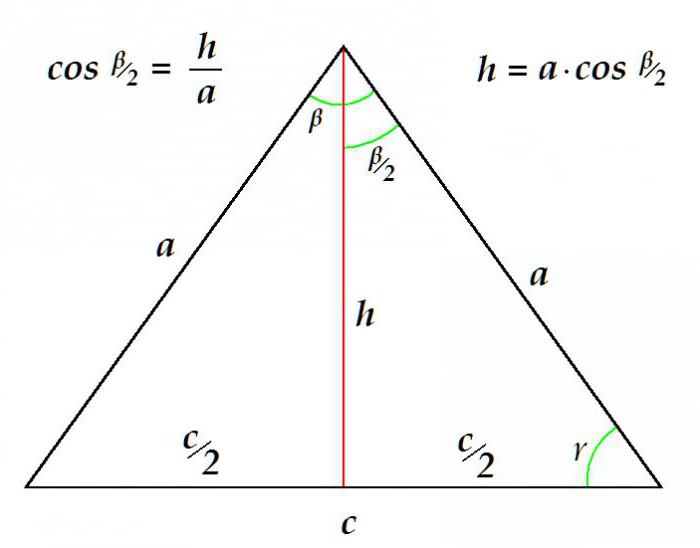
Na primjer, možete odrediti duljinu medijana prema poznatoj strani i kut na vrhu.

Kako odrediti opseg

Budući da su u razmatranoj planimetrijskoj slici dvije strane uvijek jednake, tada je za određivanje opsega dovoljno znati duljina baze i duljina jedne od strana.

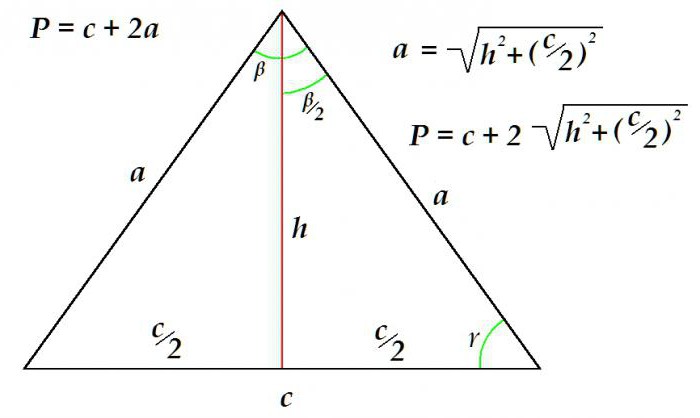
Razmotrite primjer kada definirati opseg trokuta po poznatoj bazi i visini.

Perimetar je jednak zbroju baze i dvostrukoj duljini stranice. S druge strane, strana se određuje korištenjem Pitagorina teorema kao hipotenuze pravog trokuta. Njegova duljina je jednaka kvadratni korijen zbroja kvadrata visine i kvadrata polovine baze.

Površina jednakokračnog trokuta

U pravilu postoje poteškoće i izračun površine jednakostraničnog trokuta. Univerzalno pravilo za određivanje površine trokuta kao polovine produkta baze do njegove visine, naravno, vrijedi i za naš slučaj. Međutim, svojstva jednakokračnog trokuta čine zadatak lakšim.

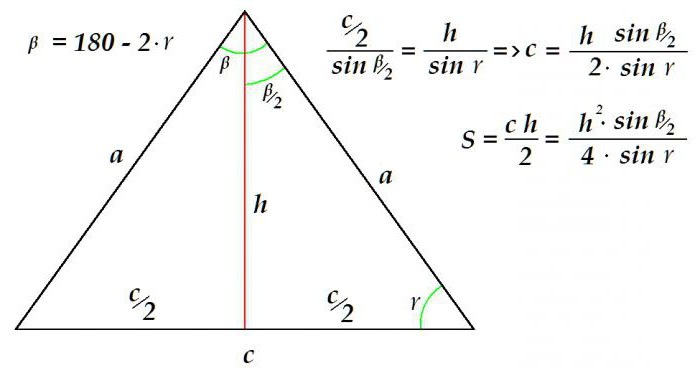
Pretpostavimo da su visina i kut uz bazu poznati. Potrebno je odrediti područje slike. To se može učiniti na ovaj način.

Budući da je zbroj kutova bilo kojeg trokuta 180 °, tada je lako odrediti kut. Nadalje, koristeći udio sastavljen prema sinusnom teoremu, određuje se duljina baze trokuta. Sve, osnovica i visina - dostatni podaci za određivanje područja - su dostupni.

Ostala svojstva jednakokračnog trokuta

Položaj središta kružnice opisan oko jednakokračnog trokuta ovisi o kutu vrha. Dakle, ako je jednakokračan trokut akutan, središte kruga nalazi se unutar figure.

Središte kruga, koje je opisano oko jednolikog trokuta s tupim stranicama, leži izvan njega. I konačno, ako je kut na vrhu 90 °, centar se nalazi točno na sredini baze, a promjer kruga prolazi kroz samu bazu.

Da bi se odredio radijus kružnice opisan oko jednakokračnog trokuta, dovoljno je podijeliti duljinu strane s dvostrukim kosinusom od pola kuta na vrhu.