Ravnomjerno ubrzano kretanje. Zadaci i formule

Najvažnija karakteristika pokreta tijela je njegova brzina. Znajući to, kao i neke druge parametre, uvijek možemo odrediti vrijeme kretanja, prevaljenu udaljenost, početnu, konačnu brzinu i ubrzanje. Jednako ubrzano kretanje je samo jedna vrsta gibanja. To se obično javlja u problemima iz fizike iz kinematičke sekcije. U takvim zadacima se uzima tijelo materijalna točka što uvelike pojednostavljuje sve izračune.

Brzina. ubrzanje

Prije svega, želio bih skrenuti pozornost čitatelja na činjenicu da ove dvije fizikalne veličine nisu skalarne, nego vektoralne. A to znači da pri rješavanju određenih vrsta problema treba obratiti pozornost na to kakvo ubrzanje tijelo ima u smislu znaka, a što je vektor brzine tijela. Općenito, u trenucima isključivo matematičkog plana takvi trenuci su izostavljeni, ali u fizici je to vrlo važno, jer u kinematičkim, zbog jednog pogrešno danog znaka, odgovor može biti pogrešan.

primjeri

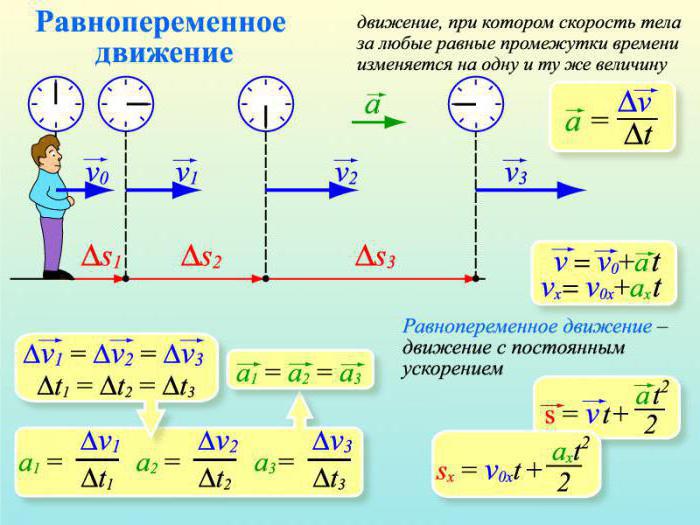
Kao primjer, možete uzeti jednoliko ubrzano i jednako lagano gibanje. Jednako ubrzano kretanje karakterizira, kao što je dobro poznato, ubrzanje tijela. Ubrzanje ostaje konstantno, ali brzina se stalno povećava u svakoj pojedinoj točki u vremenu. Uz jednako usporeno kretanje, ubrzanje ima negativnu vrijednost, brzina tijela se kontinuirano smanjuje. Ova dva tipa ubrzanja temelj su mnogih fizičkih problema i često se susreću u problemima prvog dijela testova iz fizike.

Primjer ravnomjerno ubrzanog kretanja

Jednako ubrzano kretanje susrećemo se svaki dan svugdje. Nijedan se automobil ne kreće ravnomjerno u stvarnom životu. Čak i ako brzinomjer pokazuje točno 6 kilometara na sat, treba shvatiti da to zapravo nije slučaj. Prije svega, ako analiziramo ovo pitanje s tehničkog stajališta, prvi parametar koji će dati netočnost bit će uređaj. Umjesto toga, njegova pogreška.

Sve ih susrećemo Mjerni i kontrolni instrumenti. Isti redak. Uzmite oko deset komada barem isti (15 centimetara svaki, na primjer) vladara, iako različite (15, 30, 45, 50 centimetara). Pričvrstite ih jedni drugima, i primijetit ćete da postoje male netočnosti, a njihove skale se ne podudaraju. To je pogreška. U ovom slučaju, to će biti jednako polovici cijene podjele, kao i drugim instrumentima koji proizvode određene vrijednosti.

Drugi čimbenik koji će dati netočnost je skala uređaja. Brzinomjer ne uzima u obzir vrijednosti kao što su pola kilometra, jedan kilometar i tako dalje. Primijetiti na uređaju dovoljno je teško oko. Gotovo nemoguće. Ali postoji promjena brzine. Dopustite na tako malu količinu, ali još uvijek. Dakle, to će biti jednoliko ubrzano kretanje, a ne jednoliko. Isto se može reći i za uobičajeni korak. Idemo, recimo, hodamo, a netko kaže: naša brzina je 5 kilometara na sat. Ali to nije posve točno i zašto, rečeno je malo više.

Ubrzanje tijela

Ubrzanje može biti pozitivno i negativno. To je ranije spomenuto. Dodamo da je ubrzanje vektorska količina koja je brojčano jednaka promjeni brzine u određenom vremenskom razdoblju. To jest, preko formule, može se označiti na sljedeći način: a = dV / dt, gdje je dV promjena brzine, dt je vremenski interval (promjena u vremenu).

nijanse

Odmah se može postaviti pitanje kako ubrzanje u ovoj situaciji može biti negativno. Oni koji postavljaju slično pitanje motiviraju je činjenicom da čak ni brzina ne može biti negativna, ne u to vrijeme. Zapravo, vrijeme ne može biti negativno. No često se zaboravlja da brzina može poprimiti negativne vrijednosti. To je vektorska količina, ne zaboravite na nju! Cijela stvar, vjerojatno, u stereotipima i pogrešnom razmišljanju.

Dakle, za rješavanje problema dovoljno je razumjeti jednu stvar: ubrzanje će biti pozitivno ako se tijelo ubrzava. I to će biti negativno ako se tijelo usporava. To je sve, dovoljno jednostavno. Najjednostavnije logičko razmišljanje ili sposobnost da se vidi između linija već će zapravo biti dio rješenja fizičkog problema vezanog uz brzinu i ubrzanje. Poseban slučaj je gravitacijsko ubrzanje i ne može biti negativan.

Formula. Rješavanje problema

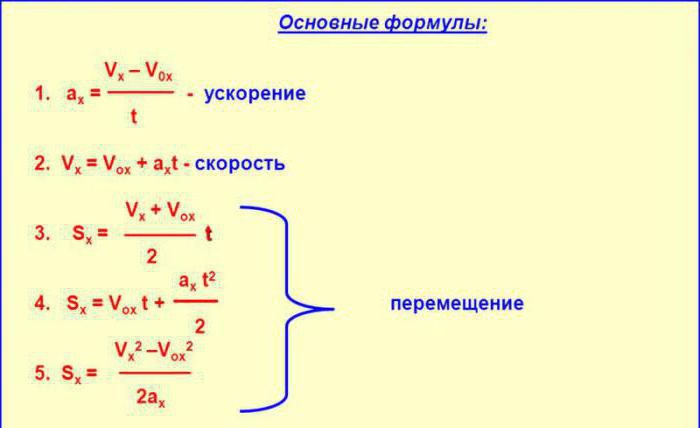
Treba shvatiti da su zadaci povezani s brzinom i ubrzanjem ne samo praktični, već i teoretski. Stoga ćemo ih analizirati i, ako je moguće, pokušati ćemo objasniti zašto je ovaj ili onaj odgovor točan ili, naprotiv, pogrešan.

Teorijski problem

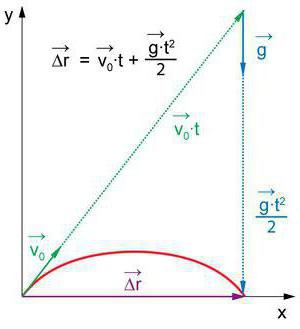
Vrlo često na ispitima iz fizike u devetom i jedanaestom razredu mogu se susresti takva pitanja: "Kako će se tijelo ponašati ako je zbroj svih sila koje djeluju na nju nula?". Zapravo, formulacija pitanja može biti vrlo različita, ali je odgovor i dalje isti. Prvo što treba učiniti je pokrenuti površinske zgrade i uobičajeno logično razmišljanje.

Izbor učenika daje 4 odgovora. Prvo: "brzina će biti nula". Drugi: "brzina tijela se smanjuje tijekom vremena". Treće: "brzina tijela je konstantna, ali nije točno nula". Četvrto: "brzina može imati bilo koju vrijednost, ali u svakom trenutku vremena bit će konstantna".

Točan odgovor ovdje je, naravno, četvrti. Sada ćemo vidjeti zašto. Pokušajmo razmotriti sve opcije. Kao što je poznato, zbroj svih sila koje djeluju na tijelo je proizvod mase i ubrzanja. Ali masa ostaje konstantna, odbacujemo je. To jest, ako je zbroj svih sila nula, ubrzanje će također biti nula.

Dakle, pretpostavimo da će brzina biti nula. Ali to ne može biti, jer imamo nula ubrzanja. Čisto fizički, to je dopušteno, ali ne u ovom slučaju, jer sada govorimo o nečem drugom. Neka se brzina tijela smanji tijekom određenog vremena. Ali kako se može smanjiti, ako je ubrzanje konstantno i nula? Nema razloga i preduvjeta za smanjenje ili povećanje brzine. Stoga odbacujemo drugu opciju.

Pretpostavimo da je brzina tijela konstantna, ali nije točno nula. Stvarno će biti konstantna zbog činjenice da ubrzanje jednostavno nema. Ali ne možemo sa sigurnošću reći da će brzina biti različita od nule. No, četvrta opcija - pravo u jabuku. Brzina može biti bilo koja, ali budući da nema ubrzanja, ona će biti konstantna u vremenu.

Praktični zadatak

Odredite put kojim je tijelo putovalo u određenom vremenskom razdoblju t1-t2 (t1 = 0 sekundi, t2 = 2 sekunde) ako su dostupni sljedeći podaci. Početna brzina tijela u intervalu od 0 do 1 sekunde je 0 metara u sekundi, konačna brzina je 2 metra u sekundi. Brzina tijela od 2 sekunde također je jednaka 2 metra u sekundi.

Rješavanje sličnog problema je vrlo jednostavno, samo trebate uhvatiti njegovu bit. Dakle, morate pronaći način. Pa, počnimo tražiti, nakon odabira dva područja. Lako je vidjeti da prvi dio puta (od 0 do 1 sekunde) tijelo prolazi ravnomjerno ubrzano, o čemu svjedoči povećanje njegove brzine. Tada ćemo pronaći ovo ubrzanje. Može se izraziti kao razlika brzina podijeljena s vremenom kretanja. Ubrzanje će biti (2-0) / 1 = 2 metra u sekundi na kvadrat.

Prema tome, prijeđena udaljenost na prvoj dionici puta S bit će jednaka: S = V0t + pri ^ 2/2 = 0 * 1 + 2 * 1 ^ 2/2 = 0 + 1 = 1 metar. U drugom dijelu staze u razdoblju od 1 sekunde do 2 sekunde tijelo se ravnomjerno pomiče. Dakle, udaljenost će biti jednaka V * t = 2 * 1 = 2 metra. Sada sumiramo udaljenosti, dobivamo 3 metra. To je odgovor.