Koje su metode optimizacije? Metode optimizacije upravljačkih odluka

Najprihvatljivije rješenje koje se poduzima na upravljačkoj razini u odnosu na bilo koje pitanje smatra se optimalnim, a proces njegovog pretraživanja smatra se optimizacijom.

Međuzavisnost i složenost organizacijskih, društveno-ekonomskih, tehničkih i drugih aspekata upravljanja proizvodnjom sada je svedena na donošenje upravljačkih odluka koje utječu na velik broj različitih čimbenika koji su međusobno usko povezani, što onemogućuje analizu svakog od njih pojedinačno koristeći tradicionalnu analitičku analizu metode.

Većina čimbenika je odlučujuća u procesu donošenja odluka i (u biti) nisu podložni nikakvoj kvantitativnoj karakterizaciji. Postoje i oni koji su praktički nepromijenjeni. S tim u vezi, postalo je nužno razviti posebne metode kojima se može osigurati izbor važnih upravljačkih odluka u okviru složenih organizacijskih, ekonomskih, tehničkih zadataka (stručne procjene, operacijska istraživanja i metode optimizacije, itd.).

Metode istraživanja operacija koriste se u cilju pronalaženja optimalnih rješenja u područjima upravljanja kao što su organizacija proizvodnih i transportnih procesa, planiranje velikih razmjera. proizvodnja, materijal i tehnička opskrba.

Metode optimizacije rješenja proučavaju se usporedbom numeričkih procjena niza čimbenika, čija se analiza tradicionalnim metodama ne može provesti. Optimalno rješenje je najbolja među mogućim opcijama ekonomski sustav a najprihvatljiviji u odnosu na pojedine elemente sustava je neoptimalan.

Suština operacija istraživačkih metoda

Kao što je ranije spomenuto, oni oblikuju metode za optimiziranje upravljačkih odluka. Njihova osnova su matematički (deterministički), probabilistički modeli koji predstavljaju proces, aktivnost ili sustav koji se istražuje. Takav model predstavlja kvantitativnu karakteristiku odgovarajućeg problema. Oni služe kao osnova za uzimanje važnih upravljačke odluke u procesu pretraživanja optimalno prihvatljiva opcija.

Popis pitanja koja igraju značajnu ulogu za direktne menadžere proizvodnje i koji se rješavaju tijekom korištenja razmatranih metoda:

• stupanj valjanosti odabranih rješenja;
• koliko su bolje od alternativnih;
• stupanj razmatranja određenih čimbenika;
• koji je kriterij optimalnosti odabranih rješenja.

Te metode optimizacije rješenja (menadžerski) usmjerene su na pronalaženje optimalnih rješenja za što je moguće više tvrtki, tvrtki ili njihovih podjela. Temelji se na postojećim dostignućima statističkih, matematičkih i ekonomskih disciplina (teorija igara, čekanje, grafovi, optimalno programiranje, matematička statistika).

Metode vještačenja

Te metode optimizacije upravljačkih odluka primjenjuju se kada je zadatak djelomično ili potpuno neobjavljen, a njegovo rješenje ne može se pronaći pomoću matematičkih metoda.

Stručnost je proučavanje složenih specifičnih pitanja u fazi izrade posebne upravljačke odluke relevantnih osoba koje posjeduju posebnu bazu znanja i impresivno iskustvo za dobivanje zaključaka, preporuka, mišljenja, ocjena. U procesu stručnog istraživanja koriste se najnovija dostignuća znanosti i tehnologije kao dio specijalizacije stručnjaka.

Razmatrane metode optimizacije niza upravljačkih odluka (stručne procjene) su učinkovite u rješavanju sljedećih upravljačkih zadataka u proizvodnom sektoru:

1. Proučavanje složenih procesa, fenomena, situacija, sustava koje karakteriziraju neformalizirane, kvalitativne karakteristike.
2. Rangiranje i određivanje prema zadanom kriteriju značajnih čimbenika koji su odlučujući za funkcioniranje i razvoj proizvodnog sustava.
3. Razmatrane optimizacijske metode posebno su djelotvorne u području prognoziranja trendova razvoja proizvodnog sustava, kao i njegove interakcije s vanjskim okruženjem.
4. Poboljšanje pouzdanosti stručnih ocjena uglavnom su ciljne funkcije, koje su kvantitativne i kvalitativne prirode, usredotočujući stavove kvalificiranih stručnjaka.

A to su samo neke od metoda za optimizaciju niza upravljačkih odluka (recenziranje).

Klasifikacija razmatranih metoda

Metode rješavanja optimizacijskih problema, na temelju broja parametara, mogu se podijeliti na:

• Metode jednodimenzionalne optimizacije.
• Metode optimizacije su višedimenzionalne.

Oni se također nazivaju "numeričkim metodama optimizacije". Točnije, to su algoritmi pretraživanja.

U okviru primjene derivativnih metoda su:

• metode izravne optimizacije (nulti red);
• gradijentne metode (1. red);
• metode drugog reda, itd.

Većina višedimenzionalnih optimizacijskih metoda blizu je problema druge skupine metoda (jednodimenzionalna optimizacija).

Jednosmjerne tehnike optimizacije

Bilo koje numeričke metode optimizacije temelje se na približnom ili točnom izračunu njegovih karakteristika, kao što su vrijednosti objektivne funkcije i funkcija koje definiraju dopušteni skup, njihove izvedenice. Dakle, za svaki pojedini zadatak može se riješiti pitanje izbora karakteristika za izračun, ovisno o postojećim svojstvima predmetne funkcije, dostupnim mogućnostima i ograničenjima u pohrani i obrada informacija.

Postoje sljedeće metode za rješavanje problema optimizacije (jednodimenzionalni):

• Fibonaccijeva metoda;
• dihotomija;
• zlatni presjek;
• dvostruki korak.

Fibonaccijeva metoda

Prvo morate postaviti koordinate t. X na intervalu [a; b] kao broj jednak omjeru razlike (x - a) prema razlici (b - a). Stoga, a ima relativni interval [a; b] koordinata 0, i b - 1, sredina 1/2.

Ako pretpostavimo da su F0 i F1 međusobno jednaki i zauzimaju vrijednost 1, F2 će biti jednaka 2, F3 - 3, ..., zatim Fn = Fn-1 + Fn-2. Dakle, Fn je Fibonaccijevi brojevi, a Fibonaccijevo pretraživanje je optimalna strategija za tzv. Sekvencijalno maksimalno pretraživanje jer je s njima vrlo blisko povezana.

U okviru optimalne strategije uobičajeno je odabrati xn - 1 = Fn - 2: Fn, xn = Fn - 1: Fn. Za bilo koji od dva intervala ([0; xn] ili [xn - 1; 1]), od kojih svaki može djelovati kao suženi interval nesigurnosti, točka (naslijeđena) u odnosu na novi interval imat će ili koordinate [Fn - 3: Fn– 1] ili [Fn-2: Fn-1]. Nadalje, uzima se točka kao xn - 2, koja, s obzirom na novi razmak, ima jednu od prikazanih koordinata. Ako upotrijebimo F (xn - 2), vrijednost funkcije, koja je naslijeđena iz prethodnog jaza, postaje moguće smanjiti interval nesigurnosti i prenijeti na naslijeđe jedne funkcije.

Na završnom koraku moguće je prijeći na takav interval nesigurnosti kao [a; b], dok je sredina naslijeđena od prethodnog koraka. Kao x1, postavlja se točka koja ima relativnu koordinatu ½ + ε, a konačni interval nesigurnosti bit će [0, ½ + ε] ili [1/2, 1] u odnosu na [a; b].

Na prvom koraku duljina tog intervala smanjena je na Fn - 1: Fn (iz jednog). Na završnim koracima redukcija duljina odgovarajućih intervala prikazana je brojevima Fn - 2: Fn - 1, Fn - 3: Fn - 2, ..., F2: F3, F1: F2 (1 + 2ε). Dakle, duljina takvog intervala kao konačna verzija će uzeti vrijednost (1 + 2ε): Fn.

Ako zanemarimo ε, tada asimptotski 1: Fn će biti jednako rn, s n → ∞, a r = (√5 - 1): 2, što je približno jednako 0,6180.

Valja napomenuti da asimptotski za značajno n svaki sljedeći korak Fibonačijevog pretraživanja značajno sužava razmotreni interval s gore spomenutim koeficijentom. Taj rezultat treba usporediti s 0,5 (koeficijent sužavanja intervala nesigurnosti u okviru metode bisekcije kako bi se pronašla funkcija nula).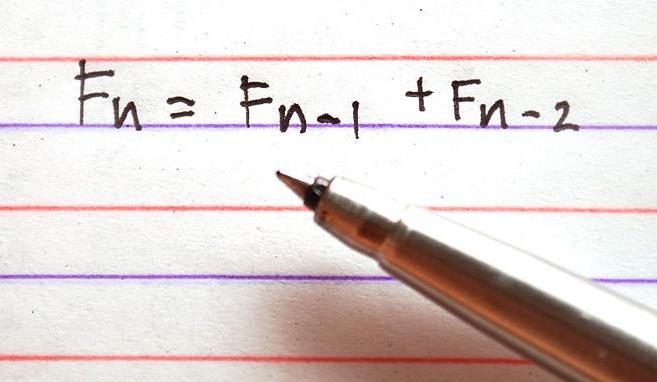

Metoda dihotomije

Ako predstavimo određenu objektivnu funkciju, tada prvo moramo pronaći njezin ekstrem u intervalu (a; b). Da bi se to postiglo, apscisa je podijeljena na četiri ekvivalentna dijela, pa je potrebno odrediti vrijednost dotične funkcije na 5 točaka. Zatim odaberite minimalni broj među njima. Ekstremum funkcije mora ležati unutar intervala (a '; b'), koji je susjedan minimalnoj točki. Granice pretraživanja sužene su 2 puta. A ako je minimum smješten u m. A ili b, onda se sužava četiri puta. Novi interval također je podijeljen u četiri jednaka segmenta. Zbog činjenice da su vrijednosti ove funkcije u tri točke određene u prethodnoj fazi, potrebno je izračunati objektivnu funkciju u dvije točke.

Metoda Zlatnog odjeljka

Za značajne vrijednosti n, koordinate točaka kao xn i xn - 1 bliske su 1 - r, jednako 0,3820, a r ≈ 0,6180. Guranje tih vrijednosti vrlo je blizu željenoj optimalnoj strategiji.

Ako pretpostavimo da je F (0,3820)> F (0,6180), onda je određen interval [0; 0,6180]. Međutim, budući da je 0.6180 * 0.6180 ≈ 0.3820 ≈ xn-1, tada je u ovoj točki F već poznato. Prema tome, u svakoj fazi, počevši od drugog, potreban je samo jedan izračun objektivne funkcije, a svaki korak smanjuje dužinu razmatranog intervala za faktor 0,6180.

Za razliku od Fibonačijevog pretraživanja, ova metoda ne zahtijeva fiksiranje broja n čak i prije početka pretraživanja.

"Zlatni dio" odjeljka (a; b) je dio u kojem je omjer njegove duljine r i većeg dijela (a; c) identičan omjeru većeg dijela r na manji, odnosno (a; c) do (c; b). Nije teško pogoditi da je r određen gornjom formulom. Stoga, uz značajan n, Fibonacci metoda ulazi u ovu.

Metoda dubliranja koraka

Suština je traženje smjera smanjenja objektivne funkcije, kretanja u tom smjeru u slučaju uspješnog pretraživanja sa postupno rastućim korakom.

Najprije odredimo početnu koordinatu M0 funkcije F (M), minimalnu vrijednost koraka h0, smjer pretraživanja. Tada definiramo funkciju u m. Zatim napravite korak i pronađite vrijednost ove funkcije u ovom trenutku.

Ako je funkcija manja od vrijednosti koja je bila na prethodnom koraku, trebate izvršiti sljedeći korak u istom smjeru, prethodno ga povećavajući 2 puta. Kada je njegova vrijednost veća od prethodne, trebat ćete promijeniti smjer pretraživanja, a zatim početi pomicati u odabranom smjeru korakom h0. Prikazani algoritam može se modificirati.

Metode višedimenzionalne optimizacije

Gornja metoda nultog reda ne uzima u obzir derivate minimizirane funkcije, tako da njihova uporaba može biti učinkovita u slučaju bilo kakvih poteškoća s izračunom izvedenica.

Skupina metoda prvog reda naziva se i gradijent, jer se gradijent ove funkcije koristi za određivanje smjera pretraživanja - vektora čije su komponente djelomični derivati ​​minimizirane funkcije s obzirom na odgovarajuće optimizirane parametre.

U skupini metoda drugog reda koriste se dva derivata (njihova je upotreba prilično ograničena zbog prisutnosti poteškoća u njihovom izračunavanju).

Popis metoda bezuvjetne optimizacije

Kada se koristi višedimenzionalno pretraživanje bez uporabe izvedenica, metode bezuvjetne optimizacije su sljedeće:

• Hook i Jeeves (provedba 2 tipa pretraživanja - na modelu i istraživanju);
• minimiziranje ispravnog simpleksa (traženje minimalne točke odgovarajuće funkcije uspoređivanjem na svakoj pojedinačnoj iteraciji njegovih vrijednosti u vrhovima simpleksa);
• cikličko spuštanje koordinata (pomoću koordinatnih vektora kao referentnih točaka);
• Rosenbrock (na temelju uporabe jednodimenzionalnog minimiziranja);
• minimiziranje deformiranim simpleksom (modifikacija metode minimiziranja redovitim simpleksom: dodavanje postupka kompresije, ekstenzija).

U situaciji korištenja izvedenica u procesu višedimenzionalnog pretraživanja razlikuje se metoda najbržeg spuštanja (najtemeljniji postupak za minimiziranje diferencijabilne funkcije s nekoliko varijabli).

Oni također razlikuju takve metode koje koriste konjugirane smjerove (Davidon-Fletcher-Powell metoda). Njezina je bit prikazivanje pravaca pretraživanja kao Dj * grad (f (y)).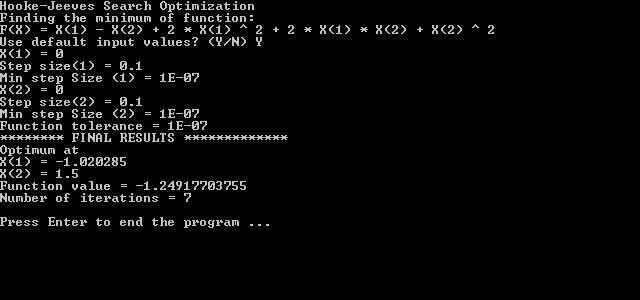

Klasifikacija matematičkih metoda optimizacije

Konvencionalno, na temelju dimenzija funkcija (cilj), to su:

• s 1 varijablom;
• višedimenzionalna.

Ovisno o funkciji (linearnoj ili nelinearnoj), postoji veliki broj matematičkih metoda koje imaju za cilj pronalaženje ekstrema za rješavanje problema.

Prema kriteriju za uporabu izvedenica, matematičke metode optimizacije dijele se na:

• metode izračunavanja 1 izvedenice ciljne funkcije;
• višedimenzionalna (1. derivacija - vektorska veličina - gradijent).

Na temelju učinkovitosti izračuna postoje:

• metode izračuna brzog ekstrema;
• pojednostavljeno računanje.

To je uvjetna klasifikacija razmatranih metoda.

Optimizacija poslovnih procesa

Ovdje se metode mogu razlikovati, ovisno o problemima koje treba riješiti. Uobičajeno je izdvojiti sljedeće metode za optimizaciju poslovnih procesa:

• iznimke (smanjenje postojećih procesnih razina, uklanjanje uzroka smetnji i ulazne kontrole, smanjenje transportnih pravaca);
• pojednostavljenja (olakšavanje prolaza narudžbe, smanjenje složenosti strukture proizvoda, raspodjela posla);
• standardizacija (korištenje posebnih programa, metoda, tehnologija, itd.);
• ubrzanje (paralelno inženjerstvo, stimulacija, operativno projektiranje prototipa, automatizacija);
• promjene (promjene u području sirovina, tehnologija, metoda rada, položaj osoblja, sustavi rada, količina narudžbe, postupak obrade);
• osiguravanje interoperabilnosti (u smislu organizacijskih jedinica, osoblja, sustava rada);
• odabir i uključivanje (u svezi s potrebnim procesima, komponentama).

Porezna optimizacija: metode

Rusko zakonodavstvo daje poreznom obvezniku vrlo bogate mogućnosti za smanjenje iznosa poreza, zbog čega je uobičajeno izdvojiti metode kojima se one smanjuju, kao što su opće (klasične) i posebne.

Opće metode optimizacije poreza su sljedeće:

• razrada računovodstvene politike tvrtke uz maksimalno korištenje mogućnosti koje pruža rusko zakonodavstvo (postupak otpisa IBE-a, izbor metode izračuna prihoda od prodaje robe, itd.);
• optimizacija putem ugovora (sklapanje povlaštenih transakcija, jasna i kompetentna uporaba riječi itd.);
• korištenje raznih vrsta naknada, poreznih olakšica.

Drugu skupinu metoda mogu koristiti i sve tvrtke, ali one još uvijek imaju prilično uski opseg. Posebne metode optimizacije poreza su sljedeće:

• zamjena odnosa (operacija, koja predviđa opterećujuće oporezivanje, zamjenjuje se drugom, što vam omogućuje postizanje sličnog cilja, ali istodobno korištenje postupka povlaštenog oporezivanja).
• razdvajanje odnosa (zamjena samo dijela poslovne transakcije);
• odgoda plaćanja poreza (odgađanje trenutka nastanka porezna stavka za drugo kalendarsko razdoblje);
• izravno smanjenje predmeta oporezivanja (uklanjanje mnogih oporezivih transakcija ili imovine bez negativnog utjecaja na glavnu gospodarsku djelatnost poduzeća).