Koji je trenutak inercije: formule za štap i kotač

Svako kretanje tijela u prostoru, čija je putanja kružnica, podrazumijeva poznavanje ne samo kutne brzine, već i trenutka inercije za opis tog kretanja. Koji je trenutak inercije, kao i ono što je jednako za štap i kotač, ovaj članak će odgovoriti.

Rotacija i moment inercije

Fizička veličina, koja se naziva moment inercije, u pravilu je označena slovom I i pojavljuje se u fizici kada se razmatra kutni moment materijalne točke, koja se rotira oko osi. Kutni moment L u skalarnom obliku ispisan je sljedećim izrazom:

L = r * m * v

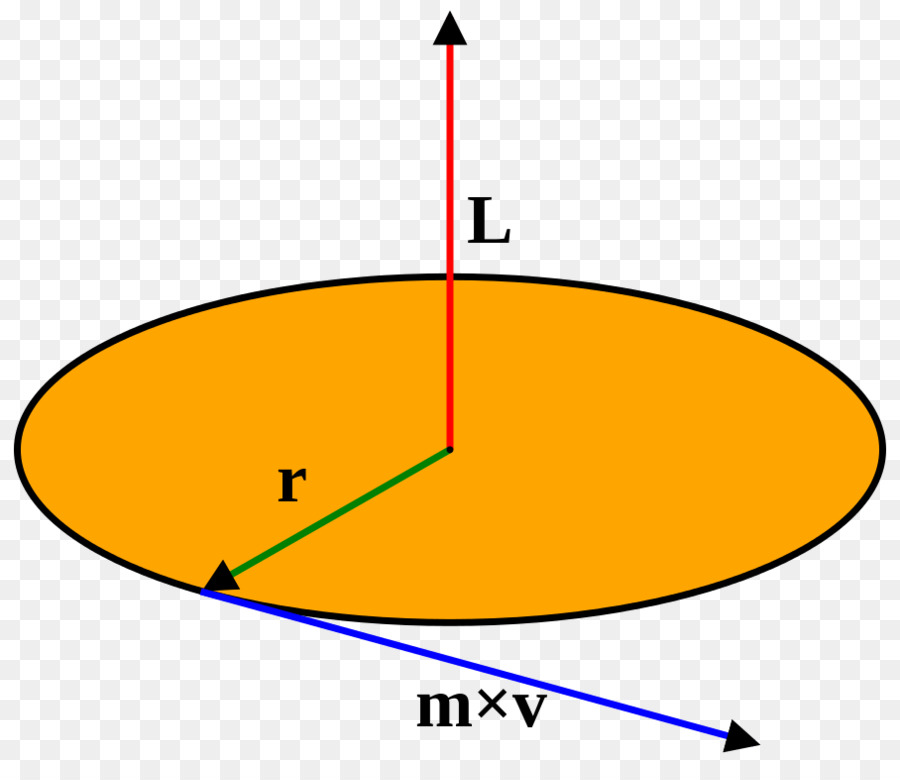
Ovdje je r udaljenost do osi materijalne točke, m je njena masa, v je linearna brzina. Koristeći odnos posljednjeg s kutnim brzinama ω, dobivamo izraz:

L = r ² * m * ω, gdje je ω = v / r

Odgovarajući na pitanje što je trenutak inercije, treba reći da je to vrijednost I = r ² * m. To jest, ovisi o masi rotirajućeg objekta, brzo raste s povećanjem udaljenosti do osi i mjeri se u kg * m ² .

Opći izraz za trenutak inercije

Formula koja se nalazi u prethodnom odlomku za vrijednost I vrijedi ako su dimenzije objekta zanemarive u odnosu na udaljenost do r osi (Zemlja se okreće oko naše zvijezde). Ako linearne dimenzije objekta postanu usporedive s udaljenosti r, tada je potrebno izračunati I da bismo koristili općenitiju formulu, koja je dana u nastavku:

I = ( _m (r ² * dm)

Pokazuje se da je integrant trenutak inercije materijalne točke. Zbroj svih trenutaka iz točaka s masom dm je ukupni trenutak inercije za cijelo tijelo.

Ova formula je moćan alat za određivanje tijela ja apsolutno bilo kojeg oblika. Prema formuli, vrijednost I je aditivna, to jest, omogućuje vam da podijelite tijelo na odvojene dijelove, izračunate njihove momente inercije, a zatim dodate rezultate kako biste dobili vrijednost tijela I.

Fizičko značenje ja

Znajući što je trenutak inercije, potrebno je reći nekoliko riječi kako njegova vrijednost utječe na ponašanje i karakteristike rotacije stvarnih objekata.

Velika vrijednost I dovodi do činjenice da se tijelo vrlo teško okreće oko osi. Da biste to učinili, morate obaviti značajan posao i uložiti značajne napore. Primjer tijela s velikim I je automobilski zamašnjak - teški metalni disk koji je čvrsto postavljen na radilicu motora. Naprotiv, ako je vrijednost sustava I mala, može se brzo odmotati i jednako brzo i jednostavno zaustaviti. Primjer za to je aluminijski naplatak kotača za bicikle.

Gornja rasprava sugerira da je moment inercije karakteriziran inercijom procesa rotacije, tj. On ima istu ulogu kao i masa tijela kada se na nju primijeni sila kako bi se dobilo ubrzanje.

Razlika između mase i momenta inercije leži ne samo u mjernim jedinicama, nego iu činjenici da je potonja funkcija rotacijskog sustava, a ne samo geometrija tijela i njegove mase.

Trenutak inercije oko osi rotacije koja presijeca centar mase šipke

Razmotrimo primjer korištenja integralne formule za rješavanje stvarnih problema. Prije svega, rješavamo jednostavan problem: tu je tanak štap dužine l i mase m. Osovina se okreće okomito na ovu šipku kroz središte mase objekta. Potrebno je odrediti vrijednost I za ovaj sustav.

Pišemo opću formulu za inerciju trenutka štapa oko osi, imamo:

I = ( _m (r ² * dm)

Budući da je os okomita na predmetno tijelo, a sama šipka je beskonačno male debljine, moguće ju je mentalno rezati u tanke slojeve s ravninama paralelnim s osi. U ovom slučaju nalazimo da se element mase dm može predstaviti sljedećom jednadžbom:

dm = ρ * s * dr

Ovdje ρ je gustoća materijala, S je poprečni presjek, koji je konstantan i teži nuli (štap je beskonačno tanak). Zamijenite ovaj izraz u općoj formuli:

I = ρ * S * ∫ ^{+ l / 2} _{-l / 2} (r ² * dr)

Imajte na umu da supstituirane granice integracije za r odgovaraju stanju problema (osa dijeli štap na dva jednaka dijela). Obavljajući integraciju, dobivamo:

I = ρ * S * (r 3/3) | ^{+ l / 2} _{-l / 2} = m * l 2/12, gdje je m = ρ * S * l

Tako je moment inercije tankog štapa, kada os prolazi kroz središte mase, 12 puta manji od onog za materijalnu točku iste mase koja se nalazi na udaljenosti l od osi.

Vrijednost I za štap s osi rotacije na kraju objekta

Razmotrite što je trenutak inercije u nešto drugačijoj situaciji. Imamo isti objekt (tanki štap), ali sada os prolazi kroz kraj. Kako će se u tom slučaju promijeniti trenutak inercije? Koristeći istu metodu cijepanja štapa i naknadnu integraciju, kao u prethodnom odlomku, dobivamo:

I = ρ * S * ∫ ^l ₀ (r ² * dr)

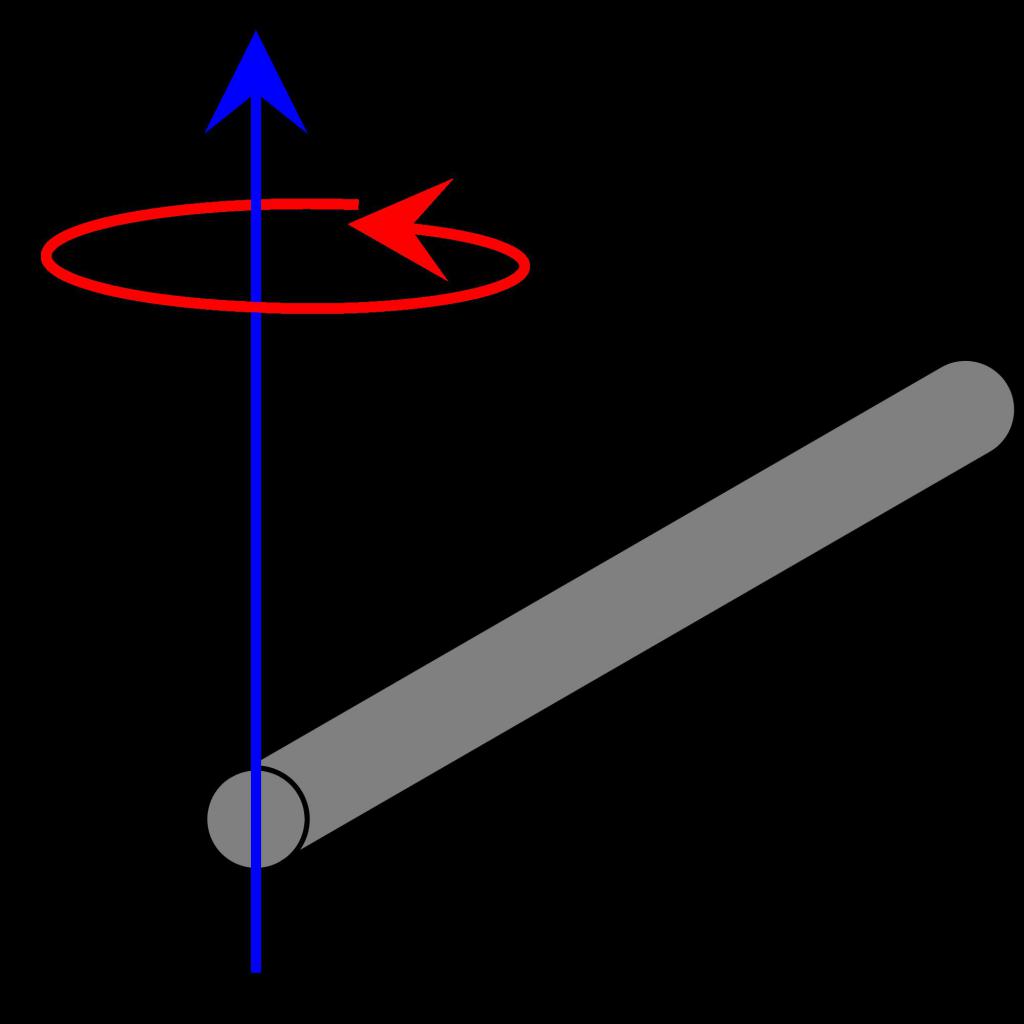
Imajte na umu da su se promijenile samo granice integracije. Rješenje je sljedeća jednakost:

I = m * l 2/3

Izraz pokazuje da će isti štap imati 4 puta veći moment inercije (teže okretati se) ako se os rotacije pomakne od središta prema rubu.

Uzimajući u obzir rješenje ova dva problema, treba napraviti važan zaključak: pri izračunavanju vrijednosti I nemoguće je smanjiti cijelu masu objekta na njegovo središte i provesti izračun kao za materijalnu točku. Izračun bi trebao biti izveden samo pomoću integralnog izraza.

Ja vrijedim za točak

Trenutak inercije kotača može se odrediti pomoću svojstva aditivnosti razmatrane količine. Da biste to učinili, mentalno rastavite kotač u zasebne dijelove, koji predstavljaju žbice i obruč. Budući da je igla tanak štap, a njegova os rotacije prolazi kroz kraj, tada je formula za nju dobivena formula iz prethodnog stavka.

Što se tiče naplatka kotača, njegov inercijski moment sličan je momentu materijalne točke koja se nalazi na udaljenosti radijusa kotača i ima masu naplatka.

Dodajući trenutke inercije svih elemenata, dobivamo:

I = n * m _c * r 2/3 + m _o * r ²

Ovdje su m _c i m _o žbice i mase oboda, n je broj žbica. Ako su sve žice teže mnogo manje od ruba, tada će inercija kotača biti jednaka:

I = m _o * r ² ako je n * m _c < o

Poznavanje vrijednosti I za kotač je važno pri izračunavanju kutne brzine i kutnog momenta rotacije kotača bilo kojeg vozila (automobila, bicikla).