Aritmetička progresija - numerički slijed

Netko je oprezan s riječju “napredovanje” kao vrlo kompliciran pojam iz dijelova više matematike. U međuvremenu, najjednostavnija aritmetička progresija je rad taksi brojača (gdje i dalje ostaju). A razumjeti bit (iu matematici ne postoji ništa važnije od "razumjeti bit") aritmetičkog slijeda nije tako teško, shvativši nekoliko osnovnih pojmova.

Matematička sekvenca brojeva

Brojčani slijed obično se naziva nizom brojeva, od kojih svaki ima svoj broj.

i ₁ - prvi član sekvence;

i ₂ - drugi član sekvence;

...

i ₇ - sedmi član sekvence;

...

i _n je n-ti član sekvence;

Međutim, ne zanima nas bilo koji proizvoljni skup brojeva i brojeva. Naša pažnja bit će usmjerena na numerički slijed, u kojem je vrijednost n-tog termina povezana s njegovim rednim brojem pomoću odnosa koji se može jasno izraziti matematički. Drugim riječima: brojčana vrijednost n-tog broja je funkcija n.

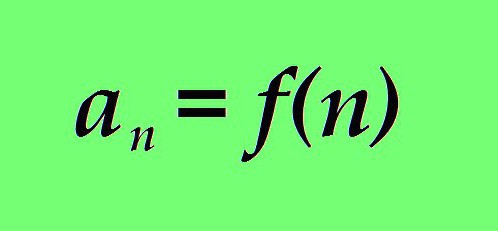
gdje je:

a je vrijednost člana numeričkog niza;

n je njegov sekvencijski broj;

f (n) je funkcija, gdje je redni broj u numeričkom nizu n argument.

definicija

Aritmetička progresija naziva se numerički slijed u kojem je svaki sljedeći pojam veći (manji) od prethodnog po istom broju. Formula za n-ti pojam aritmetičkog slijeda je sljedeća:

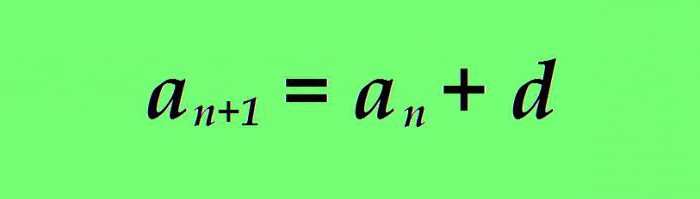
gdje

a _n - vrijednost trenutnog člana aritmetičke progresije;

a _{n + 1} je formula za sljedeći broj;

d - razlika (određeni broj).

Lako je odrediti da ako je razlika pozitivna (d> 0), onda će svaki sljedeći član razmatrane serije biti veći od prethodnog i takva aritmetička progresija će se povećavati.

primjer:

a ₁ = 5

d = 3

tada

U donjem grafikonu nije teško utvrditi zašto se brojčani slijed naziva "povećanjem".

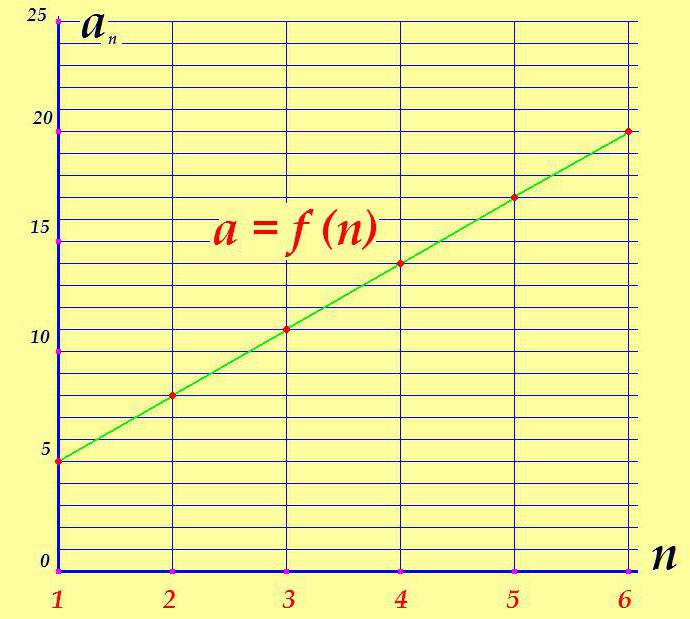
U slučajevima kada je razlika negativna (d <0), svaki sljedeći član će iz očiglednih razloga biti manji od prethodnog, grafikon progresije će se "spustiti", a aritmetička progresija će se označiti kao opadajući.

Vrijednost navedenog člana

Ponekad je potrebno odrediti vrijednost bilo kojeg proizvoljnog pojma a _n aritmetičke progresije. To možete učiniti tako da uzastopno izračunate vrijednosti svih članova aritmetičke progresije, od prvog do željenog. Međutim, takav put nije uvijek prihvatljiv ako je, primjerice, potrebno pronaći vrijednost pet tisućitog ili osammilijunskog člana. Tradicionalni izračun će trajati dugo. Međutim, određena aritmetička progresija može se istražiti pomoću određenih formula. Postoji i formula za n-ti izraz: vrijednost bilo kojeg člana aritmetičke progresije može se odrediti kao zbroj prvog termina progresije s razlikom progresije pomnoženim brojem člana koji se nalazi, umanjen za jedan.

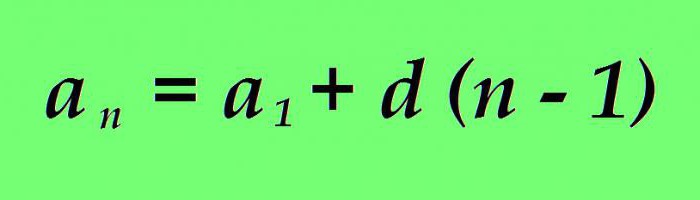
Formula je univerzalna za napredovanje uzlazno i ​​silazno.

Primjer izračuna vrijednosti određenog člana

Rješavamo sljedeći problem pronalaženja vrijednosti n-tog roka aritmetičke progresije.

Uvjet: postoji aritmetička progresija s parametrima:

prvi pojam sekvence je 3;

- razlika broja nizova je 1.2.

Zadatak: potrebno je pronaći vrijednost od 214 članova

Rješenje: za određivanje vrijednosti određenog člana koristimo formulu:

a (n) = a1 + d (n-1)

Zamjenjujući u izrazu podatke iz uvjeta problema imamo:

a (214) = a1 + d (n-1)

a (214) = 3 + 1,2 (214-1) = 258,6

Odgovor: 214. član sekvence je jednak 258.6.

Prednosti ove metode izračuna su očite - cjelokupno rješenje ne zauzima više od 2 linije.

Iznos određenog broja članova

Vrlo često, u danoj aritmetičkoj seriji, potrebno je odrediti zbroj vrijednosti određenog segmenta. Za to također nema potrebe za izračunavanjem vrijednosti svakog člana i zatim sažeti. Ova metoda je primjenjiva ako je broj članova čija je suma mala. U drugim je slučajevima prikladnije koristiti sljedeću formulu.

Zbroj članova aritmetičke progresije od 1 do n jednak je zbroju prvog i n-tog člana pomnožen brojem člana n i podijeljen na dva. Ako je u formuli vrijednost n-tog člana zamijenjena izrazom iz prethodnog stavka članka, dobivamo:

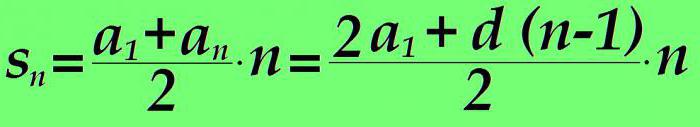
Primjer izračuna

Na primjer, riješite problem sa sljedećim uvjetima:

prvi pojam sekvence je nula;

- razlika je 0,5.

Zadatak je odrediti zbroj članova serije od 56. do 101. godine.

Odluka. Koristimo formulu za određivanje iznosa napredovanja:

s (n) = (2 1 a1 + d n (n-1)) / n / 2

Prvo definiramo zbroj vrijednosti od 101 člana progresije, zamjenjujući u formuli podatke o njihovim uvjetima našeg zadatka:

s ₁₀₁ = (2 + 0 + 0,5 ₁₀₁ (101-1)) /2 101/2 = 2 525

Očito, da bi se otkrio zbroj članova progresije od 56. do 101., potrebno je oduzeti S ₅₅ od S ₁₀₁ .

s ₅₅ = (2 + 0 + 0,5 ₅₅ (55-1)) /2 55/2 = 742,5

Tako zbroj aritmetičke progresije za ovaj primjer:

s ₁₀₁ - s ₅₅ = 2 525 - 742,5 = 1 782,5

Primjer praktične primjene aritmetičke progresije

Na kraju članka vratit ćemo se na primjer aritmetičkog slijeda navedenog u prvom odlomku - taksimetar (brojač taksi automobila). Razmotrite ovaj primjer.

Slijetanje u taksiju (koji uključuje 3 kilometra) košta 50 rubalja. Svaki sljedeći kilometar plaća se po stopi od 22 rublje / km. Udaljenost putovanja je 30 km. Izračunajte troškove putovanja.

1. Odbacite prva 3 km, čija je cijena uključena u cijenu slijetanja.

30 - 3 = 27 km.

2. Daljnji izračun nije ništa drugo nego analiza niza aritmetičkih brojeva.

Broj člana je broj prijeđenih kilometara (minus prva tri).

Vrijednost člana je zbroj.

Prvi termin u ovom problemu bit će jednak a ₁ = 50 p.

Razlika progresije d = 22 p.

broj interesa je vrijednost (27 + 1) -og člana aritmetičke progresije - očitanja brojila na kraju 27. kilometra - 27,999 ... = 28 km.

a ₂₈ = 50 + 22 ∙ (28 - 1) = 644

Formule koje opisuju određene numeričke sekvence koriste se za izračun kalendarskih podataka za proizvoljno dugo razdoblje. U astronomiji je dužina orbite u geometrijskoj ovisnosti o udaljenosti nebeskog tijela od zvijezde. Osim toga, u statistici i drugim primijenjenim granama matematike uspješno se primjenjuju različite numeričke serije.

Drugi tip brojčanog niza je geometrijski.

Geometrijsku progresiju karakterizira velika, u usporedbi s aritmetikom, brzina promjene. Nije slučajno da se u politici, sociologiji i medicini često kaže da se proces razvija eksponencijalno kako bi se pokazala visoka stopa propagiranja fenomena, na primjer, bolesti u epidemiji.

N-ti pojam geometrijskih serija brojeva razlikuje se od prethodnog po tome što se množi s fiksnim brojem - nazivnik, na primjer, prvi izraz je 1, nazivnik je 2, odnosno

n = 1: 1 = 2 = 2

n = 2: 2 = 2 = 4

n = 3: 4 = 2 = 8

n = 4: 8 = 2 = 16

n = 5: 16 x 2 = 32,

n = 6: 32 = 2 = 64 i tako dalje ...

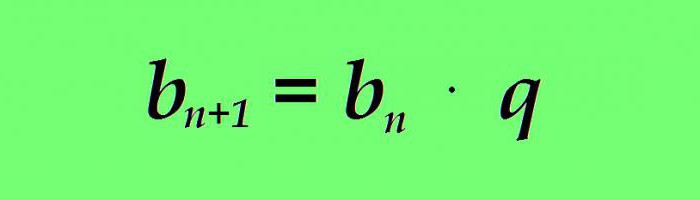
gdje je:

b _n - vrijednost trenutnog termina geometrijske progresije;

b _{n + 1} - formula za sljedeći pojam geometrijske progresije;

q je nazivnik geometrijske progresije (konstantni broj).

Ako je graf aritmetičke progresije ravna linija, onda geometrijska crta nešto drugačiju sliku:

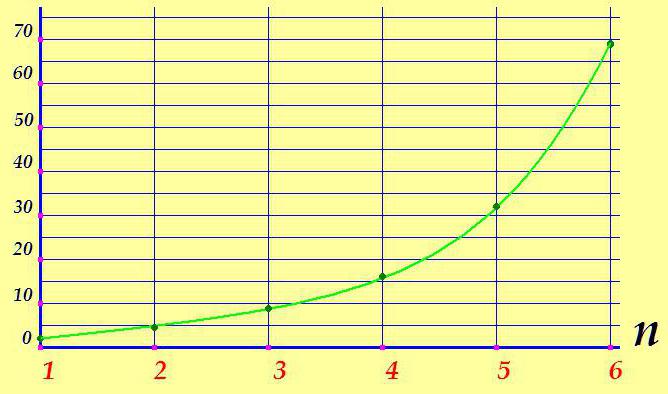
Kao iu slučaju aritmetike, geometrijska progresija ima formulu za vrijednost proizvoljnog termina. Bilo koji n-ti pojam geometrijske progresije jednak je proizvodu prvog termina nazivnikom progresije do stupnja n reduciranog za jedan:

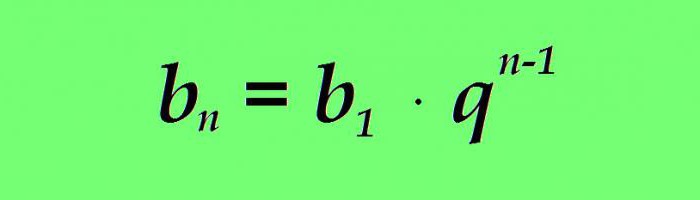
Primjer. Imamo geometrijsku progresiju s prvim pojmom jednakim 3, a nazivnik progresije jednak je 1,5. Pronađite 5. člana progresije

b ₅ = b ₁ ⁽ q ^(5-1) = 3 ⁴ 1,5 ⁴ = 15,1875

Zbroj određenog broja članova izračunava se i pomoću posebne formule. Zbroj n prvih pojmova geometrijske progresije jednak je razlici proizvoda n-tog pojma progresije po nazivniku, a prvi pojam progresije podijeljen s imeniteljem smanjen za jedan

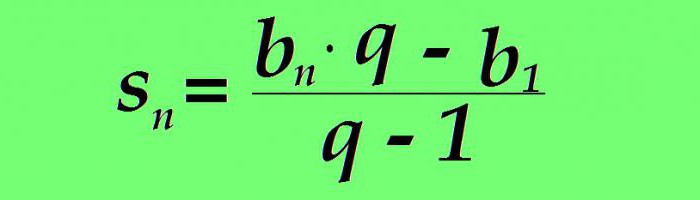
Ako se b _n zamijeni korištenjem gornje formule, vrijednost zbroja n prvih članova razmatranih serija brojeva poprima oblik:

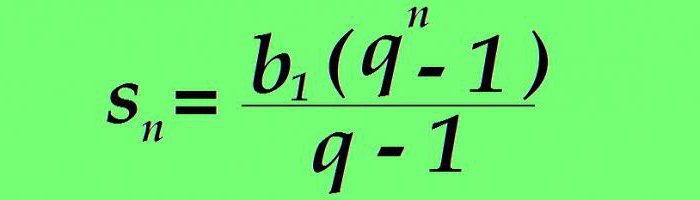
Primjer. Geometrijska progresija počinje s prvim pojmom jednakim 1. Nazivnik je postavljen na 3. Nađi zbroj prvih osam članova.

s8 = 1 ∙ (3 ⁸ -1) / (3-1) = 3 280