Centrifugalna sila - neprijatelj ili saveznik

Onaj tko je upoznat Stari zavjet Sveto pismo, lako se sjećati priče o bitci između Davida i Golijata. Strašni div bio je ubijen uz pomoć praćke. No, remen je potpuno stvarni predmet, najjednostavniji uređaj, oružje koje je korišteno u vrijeme kada se pramac smatrao naprednom tehnikom. Najstariji artefakti pronađeni tijekom iskopavanja, klasificirani kao sling, stari su deset tisuća godina. Moram reći da, unatoč izuzetno jednostavnom uređaju, remen nije bio tako bezopasan. Kamen, koji je rukom iskusnog metalca pušten iz praćke, odletio je prema neprijatelju brzinom od oko stotinu metara u sekundi. Maksimalna stvarno zabilježena udaljenost bila je veća od 400 metara.

Koji se fizikalni zakoni temelje na tako impresivnim rezultatima? Odgovor: Početna brzina prema kamenu (a kasnije i metalni kuglasti projektil) dala je upravo ta tajanstvena centrifugalna sila, koja nije jasna odakle. Osim praga, ovaj fizički fenomen bio je osnova za stvaranje mnogo više i mnogih drugih strojeva i mehanizama koje je koristio čovjek.

Opis sile sa stajališta fizike

Vrlo često, ljudi, a ponekad i zastrašujuće, čak i studenti tehničkih sveučilišta koriste takav izraz kao centripetalna sila u razgovoru, identificirajući je centrifugalnom silom. Naravno, ta dva pojma imaju mnogo zajedničkog, iako to nipošto nije ista stvar. Da bismo bolje shvatili o kojim fenomenima govorimo, moramo se sjetiti male školske fizike.

Što je inercija. Okretni metak teži oko 9 grama. Ako ga bacite oko metra i zatim ga uhvatite rukom (brzina manja od 1,0 m / s), možete osjetiti lagani trzaj. Isti je metak ispaljen iz oružja i letio brzinom od oko 500 m / s. lako se probija kroz borovu ploču debljine jednog inča. I na kraju, komadić svemirskih ostataka iste mase koji leti u orbiti prva kozmička brzina (8 000 m / s.), Poput komada maslaca, lako će probiti teški spremnik.

Bilo koje tijelo s masom m i koje se kreće brzinom V ima kinetička energija :

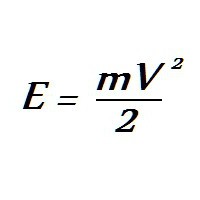
Za bačene metke:

E = 0,009 2 1 2/2 = 0,0045 J.

Za pištolj s paljenjem:

E = 0,009 2 500 2/2 = 1 125 J.

Za svemirske ostatke:

E = 0,009 000 8 000 2/2 = 288 000 J

Da bi se pokretno tijelo zaustavilo, potrebno je primijeniti istu energiju; da bi se nepomično tijelo raspršilo na takvu brzinu, potrebno je potrošiti istu energiju.

Sada zamislite da je određeno tijelo, koje leti u ravnoj liniji, prisiljeno promijeniti smjer kretanja.

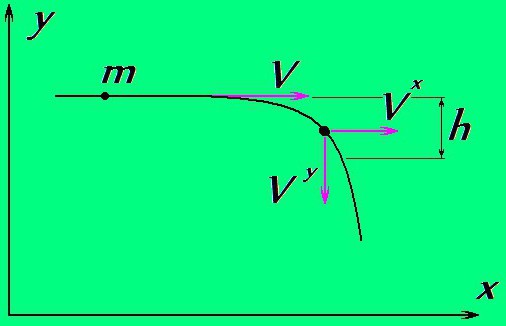
Tijelo prikazano na slici ima brzinu u smjeru osi x - V ^x , promjenom smjera kretanja daje joj brzinu u smjeru osi ordinate - V ^y , na kojoj je, prema tome, potrebno trošiti energiju:

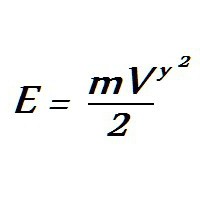
Konačno, naoružani znanjem inercije, možete se vratiti u remen. Ukratko, to je kamen (opterećenje), koji se okreće po kružnoj stazi na niti.

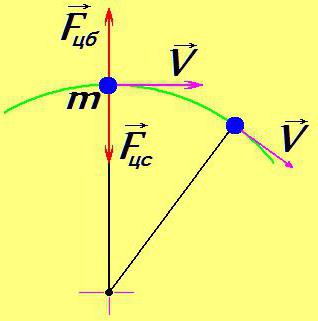
Tijelo s masom m, ne drži svoju nit, letjet će ravno (što je, u stvari, iskusio Golijat), ali držanje konca stalno mijenja svoj smjer. Očito, to se događa pod djelovanjem neke sile, koja se obično naziva centripetalna sila - F _cc . U ovom slučaju, to je sila napetosti niti.

Ali zašto u ovom slučaju kamen ne ulazi u ruku slingera? Razlog je treći zakon briljantnog Newtona, koji kaže da svaka sila koja se primjenjuje na objekt generira reakcijsku silu jednaku veličinom i suprotnom smjeru. Tako nastaje centrifugalna sila F _cb .

Životni primjeri

Nije slučajno da se na početku članka razmatra remen - najjednostavniji primjer djelovanja centrifugalne sile, koji je lakše simulirati, pokušati i osjetiti. No, osim toga, ova fizička količina prisutna je u brojnim stvarima i predmetima koji nas svakodnevno okružuju. Dakle, centrifugalna sila, koja radi u zavojima sigurnosnih pojaseva, čini putovanje sigurnim.

Ljubitelji ribolova ne bi uopće mogli raditi svoj omiljeni hobi bez te moći i onda nam govoriti besmislice. Na primjer, bacanje teškog korita - jedan na jedan imitacija borbenih remena. A predenje ili šarana u ruci ribara nije ništa drugo nego isto oružje, samo umjesto smrtonosnog kamena - žlica, vobler ili šablona.

Kako izračunati centrifugalnu silu

Skalarna veličina centrifugalne sile izračunava se pomoću formule:

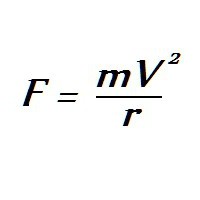
gdje je:

F - željena vrijednost centrifugalne sile, H;

m je tjelesna težina, kg;

V - brzina kretanja tijela, m / s;

r je radijus rotacije, m

Primjeri izračuna

Izračunamo silu s kojom se kamen izbacuje iz remena: dužina pojasa je 1 metar od ruke remena do kreveta. Ratnik okreće oružje brzinom od 2 okretaja u sekundi. U remenu je kamen težak 200 grama.

obujam :

L = 2πR = 2 4 3.14 1 = 6.28 m.

Tako drugi kamen leti 2 2 L = 6,28 2 = 12,56 m, to je njegova brzina - 12,56 m / s.

Tražena vrijednost je sljedeća:

F = mV ² / r = 0,2 kg .5 12,56 2/1 = 31,55 N.

Prisilno puštanje u rad

Postoji mnogo primjera gdje centrifugalna sila čini koristan rad. Osim borbe za bacanje oružja, izvrsno djeluje iu modernim sportovima. Tehnika bacanja čekića i, u manjoj mjeri, disk se zasniva na tome da brzina projektila bude precizno odmotana.

Tisuće različitih strojeva imaju princip rada koji se temelji na upotrebi centrifugalne sile. Nema potrebe ići daleko, samo zapamtite ime jedne od najčešćih vrsta crpki. A ime je "centrifugalno". Unutar tzv "Pužni" kotač s noževima okreće neku vrstu radnog fluida (tekućina ili plin). Nakon toga, zbog centrifugalnih sila, formira se povišeni tlak na vanjskoj stijenci obujma pumpe, a smanjena površina se formira u središtu pužnice, gdje je brzina vrtnje minimalna. Na taj način, transportirani medij, koji je ušao u šupljinu pumpe kroz mlaznicu u središnjem dijelu, izbačen je pod tlakom kroz izlaz u vanjskom zidu.

A ovo je samo jedan primjer. Centrifugalne sile rade u svim vrstama strojeva za čišćenje u poljoprivredi. Princip odvajanja (razdvajanja) rasutih materijala temelji se na razlici energije proizvedene česticama zbog različite gustoće i mase.

I, na kraju, primjer najživotnijeg života, za razmišljanje o kojem ne trebate ići na stadion ili u žitni utor. Pogledajte kako najobičnija perilica radi na okretanju. Posteljina se pritisne uz stjenke bubnja zbog centrifugalne sile, tako da nakon pritiska na 1000 o / min. rublje dobiva gotovo suh automobil.

Kad se bore s njom

Ali ne uvijek centrifugalna sila je poželjna. U nekim slučajevima se mora boriti. Pojedinosti velikih veličina u alatnim strojevima, brodskim mehanizmima u motorima rudarski kamioni doživljava tijekom rotacije ogromna opterećenja. Svaki više ili manje teški konstrukcijski element, pričvršćen na rotirajuću bazu, ima tendenciju da se skine i odleti u smjeru suprotnom od središta rotacije. Na primjer, oštrice helikoptera - uglavnom cijela znanost.

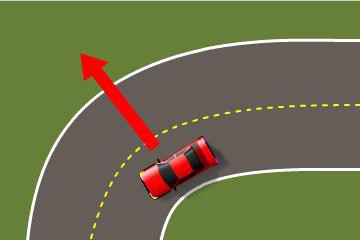
Svaki vozač zna da na klizavoj cesti automobil također puše u smjeru suprotnom od zakrivljenosti platna. Ponekad možete vidjeti kako na najoštrijim uglovima graditelji cesta posebno čine pristranost prema središtu zakrivljenosti.

Centrifugalna sila u prirodi

Jasan primjer ispoljavanja centrifugalne sile u prirodi može poslužiti kao oseka i toka u ekvatorijalnim područjima. Činjenica je da se ne okreće samo mjesec oko Zemlje. Naš planet, iako mnogo teži od satelita, još uvijek mu se malo "pleše", lagano se okrećući oko malog radijusa. To dovodi do činjenice da se u dva područja - usmjerena prema Mjesecu i suprotnom - poput grba voda svjetskog oceana formiraju.

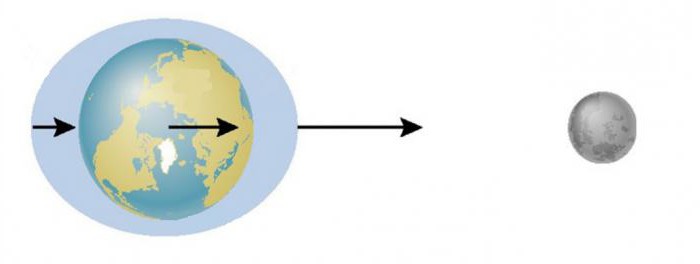
Usput, mjesec od plimnih sila dobio je više. Oni su zaustavili njegovu rotaciju oko svoje osi. Zahvaljujući centrifugalnoj sili, stanovnici plavog planeta mogu vidjeti samo jednu stranu svog prirodnog satelita.

Kratak sažetak

Tako je centrifugalna sila odgovor na centripetalnu silu. Skalarna veličina centrifugalne sile je izravno proporcionalna proizvodu tjelesne mase kvadratom njegove linearne brzine i obrnuto proporcionalna radijusu rotacije. Vektor sile prolazi kroz središte rotacije i ima smjer - od njega.