Kombinatorika - što je to? Elementi kombinatora
Stručnjaci iz različitih područja trebaju riješiti kombinacijske probleme: preraspodjelu brojeva, znakova i drugih objekata. Na primjer, voditelj trgovine mora distribuirati različite vrste rada između radnih strojeva. Kombinatorika je značajna grana matematike koja, kao što nije teško pogoditi, nalazi svoju nišu u raznim područjima i specijalnostima: fizici, biologiji, lingvistici, kemiji, inženjerstvu, teoriji kodiranja i još mnogo toga. Načela kombinatorike također su temelj rješavanja niza probabilističkih problema.
Povijest
Prvi preduvjeti kombinatorike kao znanosti pojavili su se u 16. stoljeću. Doprinos razvoju ovog područja znanja u velikoj mjeri, ljudi fasciniran kockanje: kartice, kockice, lutrija izgubili ne samo zlato i dragulje, ali palače i imanja. Stoga, pitajući se, na primjer, o tome kako često možete baciti dobar skup točaka na kosti ili dobiti dva asa, ljudi su postupno dolazili do osnova kombinatorike i vjerojatnosti. Je li kombinatorika pomogla nekome da pobijedi ili izgubi manje? Pitanje je zanimljivo, ali njegovo razmatranje je izvan dosega ovog članka.

Prvi matematičar koji je bio aktivno zainteresiran za kombinatoriku bio je talijanski talijanski Tartaglia (1499.-1557.), Nakon čega su se ugledni znanstvenici poput Pascala, Fermata, Bernoullija, Leibnitza, Eulera i drugih aktivno uključili u proučavanje tih pitanja. i dalje je ostala, ako ne i zabavna igra s brojevima, onda teorija koja se koristi isključivo u kockanju i nema pravo koristiti je drugdje.
Razvoj kombinatorika
Znatan napredak u kombinatorici dogodio se s dolaskom 20. stoljeća. računala, programiranje, i što je najvažnije - diskretna matematika. U tom razdoblju kombinatorika dobiva vrhunac svog brzog razvoja i postaje punopravna znanost. Kombinatorne metode počinju se koristiti svugdje:
- rješavanje prometnih problema;
- raspoređivanje;
- priprema planova za proizvodnju i prodaju robe;
- u teoriji slučajnih procesa;
- u matematičkoj statistici i teoriji vjerojatnosti;
- u pripremi i provođenju pokusa;
- u šahu;
- u termodinamici;
- u geometriji;
- iu mnogim drugim područjima.
Praznovjerni izazov vođe
Postojao je jedan vođa na svijetu koji je vjerovao da mu broj 8 donosi totalne neuspjehe. Stoga se odlučio riješiti svih brojeva koji bi sadržavali brojku osam. Pod njegovim nadzorom radilo je 600 ljudi. Svi su imali identifikacijski broj propusnica za rad, koja se sastoji od tri broja. Ne razmišljajući dvaput, menadžer je odlučio isključiti broj 8 iz broja propusnica, a onda se pitao ima li dovoljno različitih brojeva za 600 ljudi iz raspona od 000 do 999, što ne bi uključivalo 8?
Očito rješenje ovog problema je ručno ispisati sve brojeve od 000 do 999 i precrtati one brojeve u kojima ih ima osam. Je li moguće riješiti problem na jednostavniji način? Ako, za 999 brojeva, zadatak s nabrajanjem svih varijanti izgleda izvedivo, tada će raspon od 000000 do 999999 zahtijevati mnogo veći napor. To je ušteda vremena i truda dizajniranih kombinatorika formula.
Rješenje problema praznovjernog vođe
Drugo rješenje je kako slijedi. Uklanjanjem 8 iz niza, dobivamo da su 0, 1, 2, 3, 4, 5, 6, 7, 9 - ovih devet brojeva valjani. Nakon toga, trebali biste pronaći sve dvoznamenkaste brojeve koji ne bi sadržavali 8. To je učinjeno jednostavno: morate uzeti bilo koji broj iz valjanog i dodati mu bilo koji broj iz valjanog. Tako ćemo lako dobiti sve dvoznamenkaste brojeve koji odgovaraju stanju. Kao rezultat toga, dobivamo da svaka pojedinačna znamenka daje 9 različitih dvoznamenkastih brojeva. Ukupan broj takvih znamenki bit će 9 * 9 = 9 2 = 81.
Nastavljajući analogiju, možemo zaključiti da je za dobivanje svih troznamenkastih brojeva bez osmica potrebno postojećim dvoznamenkastim brojevima dodijeliti i treću znamenku, također iz dopuštenih vrijednosti. Tada ćemo vidjeti da će broj takvih brojki biti 9 2 * 9 = 9 * 9 * 9 = 729. Tako smo otkrili da će naša voditeljica lako moći osigurati 600 radnika s prazninama, čiji brojevi neće sadržavati 8. Pokušajte sami riješiti problem za sebe. s pet-znamenkasti broj.
I što će se dogoditi ako upravitelj ne voli broj 2? Ispada, tada će broj dopuštenih brojeva biti 8, odnosno: 0, 1, 3, 4, 5, 6, 7, 9. Zatim, nakon što je procijenio broj kombinacija brojeva bez 2 i 8, možemo zaključiti da je njihov broj 8 * 8 * 8 = 512, a to očito nije dovoljno za 600 osoba s prolazima. Kombinatorika je znanost koja pomaže odgovoriti na takva pitanja učinkovitije nego što se može učiniti brutalnom silom.
Loto problem
Svatko zna igru. Tu je i vrećica u kojoj se nalaze bačve s brojevima od 1 do 90. Ulaznice se distribuiraju svim sudionicima, u kojima je potrebno slikati preko određenog broja ćelija s brojevima. Nakon toga, vodeći loto izlazi iz vreće jedan od brojeva. Pobjednik će biti onaj koji je prekrižio većinu brojeva u ulaznici, što se podudara s onima koje je domaćin igre izvukao.

Jednom Nina, igrajući loto, pomisli. Često je gledala kako voditelj dobiva isti broj iz vrećice. Ali u isto vrijeme, prve dvije bačve pokazale su se mnogo manje. Zatim se zapitala koliko načina možete dosljedno dobiti dvije bačve iz vrećice? Elementi kombinatorike pomažu odgovoriti na njezino pitanje.
Loto rješenje
Očito, prva bačva može imati brojeve od 1 do 90. Drugim riječima, postoji 90 načina za izdvajanje prve bačve. Ali što je sljedeće? Ako je, na primjer, bačva br. 63 uklonjena iz vrećice, tada se u trenutnoj igri više neće ponoviti.
Metoda tablice pomoći će nam u rješavanju problema. U naslovu iu zaglavlju će biti ispisani brojevi stupaca od 1 do 90. Tako će na sjecištu bilo kojeg pravca i bilo kojeg stupca biti par brojeva, ili par bačvi uklonjenih iz vrećice. U isto vrijeme na dijagonali stola nalaze se isti parovi brojeva. To je nemoguće prema stanju, jer nakon uklanjanja jedne znamenke iz vrećice, njegovo ponavljanje nije moguće. Nabavite tablicu u sljedećem obliku:
| 1 | 2 | ... | 90 | |
| 1 | x | 1, 2 | ... | 1, 90 |
| 2 | 2, 1 | x | ... | 2, 90 |
| ... | ... | ... | x | ... |
| 90 | 90, 1 | 90, 2 | ... | x |
Ukupno dobivamo tablicu, u kojoj je broj ćelija 90 * 90 = 8100. Treba imati na umu da na dijagonali ima 90 parova znamenki, koje je nemoguće prema uvjetima. Tada će odgovor na pitanje koliko načina možete dobiti iz dvije vreće biti 8100 - 90 = 8010 opcija.
Zamišljajući malo drugačiji način možete doći do istog odgovora. Za prvu bačvu postoji 90 opcija. Nakon što je prvo izvađeno, preostaje 89 opcija za drugu bačvu. Dakle, ukupan broj opcija bit će 90 * 89 = 8010. Elementi kombinatorika mogu se koristiti na različite načine. Jedino je pitanje jednostavnost i univerzalnost metode. Primjerice, metoda tablice može se koristiti za tri bačve koje treba izvaditi u nizu i, očito, to će biti granica. A što za četiri ili više?
Problem s posadom
Ako izbor ovisi o tome koji su objekti ranije odabrani, onda je prikladno prikazati takav proces kao "stablo". U prvom koraku, koliko je linija postavljeno iz jedne točke jer postoje mogući izbori u prvom koraku. Na krajevima svakog retka nalazi se i više dodatnih linija koje se mogu napraviti u drugom koraku, itd. Kao rezultat toga, nacrtat će se vrsta stabla ili grafikona. Kombinatorika i teorija mogu zvučati zbunjujuće i nerazumljivo, pa pogledajmo primjer.
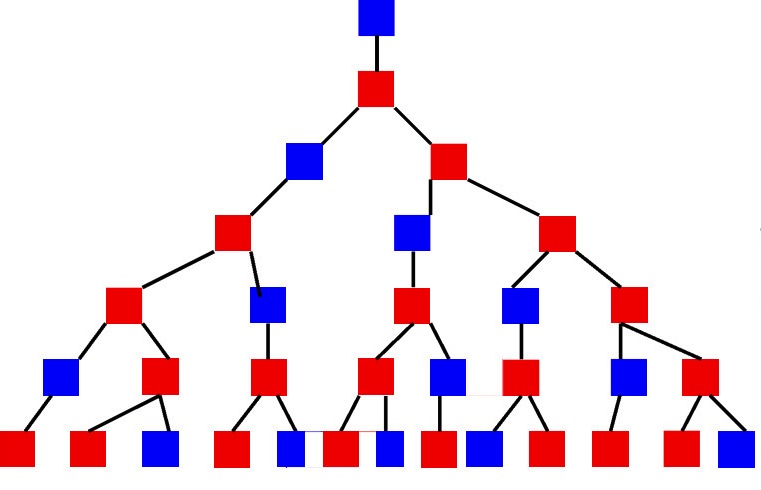
Prije početka ekspedicijske godine, vodstvo ima zadatak - skupljati posade za putovanja. Svaka ekipa mora imati tri osobe: zapovjednik, inženjer i liječnik. Istovremeno, broj stručnjaka u određenom području može varirati. Dopušteno je, primjerice, da se jedan liječnik pošalje u dvije različite ekspedicije, budući da postoje samo dva liječnika, a može biti po tri u svakom zapovjedniku i inženjeru. U tom slučaju, sastavljač ekspedicijskog plana mora uzeti u obzir psihološku kompatibilnost članova tima. Ova karakteristika je jedna od najvažnijih u dugim i udaljenim ekspedicijama za njihovo uspješno ponašanje. Na temelju svih opisanih uvjeta pojavljuje se sljedeća slika:
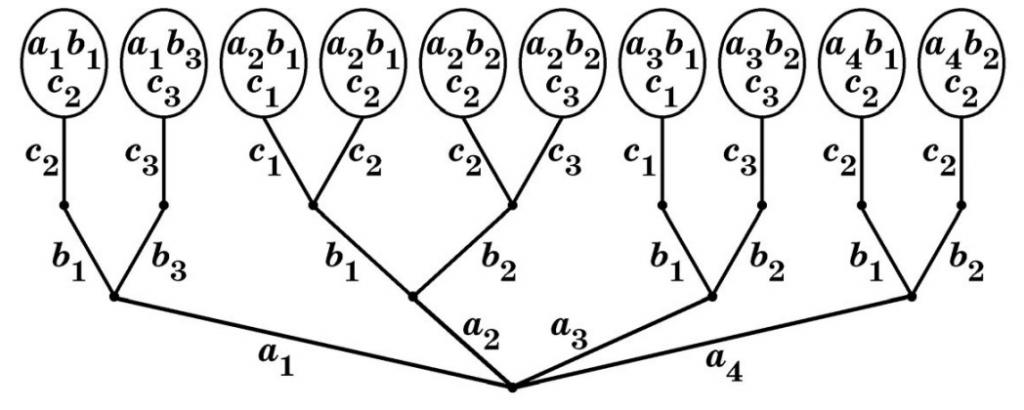
Gdje su ja zapovjednici, b i su inženjeri, a ja sam liječnici. Istovremeno, tijekom ispitivanja svake osobe, utvrđeno je da se zapovjednik a 1 psihički dobro slaže s inženjerima b 1 i b 3 , a 2 - s b 1 i b 2 , ali je liječnik c 3 nespojiv s inženjerom b 1 , itd. Pitanje koje je izvorno postavljeno voditelju projekta je koliko se posada može sastaviti pod takvim uvjetima. Iz grafikona se može vidjeti da može biti ukupno 10 takvih posada, ali što bi se dogodilo da pitanje psihološke kompatibilnosti nema težinu? Tada se ispostavlja da će nakon izbora zapovjednika ai postojati 3 alternative za svakog od njih u izboru inženjera. Prema tome, za par zapovjednika i inženjera također bi postojale 3 opcije za liječnike. Tada će broj kombinacija doseći 4 * 3 * 3 = 36 posada.
Položaji, permutacije i kombinacije
U gore navedenim primjerima rješenje problema nastalo je tzv. Aksiomatskom metodom. Naime, može se reći da postoji niz temeljnih zadataka, čije se rješavanje može svesti na mnoge probleme. Međutim, baš kao iu stereometriji, nije prikladno rješavati probleme koji se temelje isključivo na aksiomima, a za to se koristi prikladniji alat nazvan “teoremi”, pa je u kombinatorici prikladnije koristiti općenitije i dokazane metode. Tijekom višestoljetnog proučavanja kombinatorike, postalo je očito da se brojni zadaci češće susreću od drugih, te su razdvojeni u zasebne klase i dobili su svoja imena, postajući glavna kombinatorika - odnosno, rasporedi, permutacije i kombinacije.

Kombinatorni problemi
Jedan od ključnih problema kombinatornih metoda je određivanje koji skup zadataka treba smatrati kombinatornim. To se ne može strogo definirati zbog iznimno velikog broja problema koji spadaju u kombinatornu kategoriju. I onda, mnogi zadaci mogu se odnositi na kombinatoriku, kao i na drugo područje, biti susjedni ili granični.

U pojednostavljenom slučaju, može se primijetiti da kombinatorna matematika uključuje probleme koji uključuju uzorke i lokacije objekata. Istodobno, kombinatoriku karakterizira rad isključivo s konačnim skupom objekata. Na temelju tih odredbi možemo razlikovati sljedeće zadatke karakteristične za kombinatoriku:
- Napravite odabir objekata, uzimajući u obzir sva svojstva.
- Dokazati ili opovrgnuti postojanje uzorka pod određenim uvjetima.
- Pronađite broj mogućih kombinacija.
- Pronađite sve kombinacije i odredite algoritam za njihovo popisivanje.
- Pronađite optimalno rješenje problema pod danim uvjetima.
Ako se dotični problem može dodijeliti jednom od ovih tipova, onda je kombinatorni i kombinatorne formule pomoći će ga riješiti.