Razlaganje kvadratnih trodimenata na čimbenike: primjere i formule

Raspad kvadratnih trimestera na čimbenike odnosi se na školske zadatke s kojima se svatko suočava prije ili kasnije. Kako to učiniti? Koja je formula za dekompoziciju kvadratnih faktora? Korak po korak shvatit ćemo pomoću primjera.

Opća formula

Rastavljanje kvadratnih trodimenata na faktore provodi se rješavanjem kvadratne jednadžbe. To je jednostavan zadatak koji se može riješiti s nekoliko metoda - pronalaženje diskriminantnog, koristeći Vieta-teorem, postoji i grafičko rješenje. Prve dvije metode proučavaju se u srednjoj školi.

lx ² +kx+n=l(xx ₁ )(xx ₂ ) (1) Opća formula je sljedeća: lx ² + kx + n = l (xx ₁ ) (xx ₂ ) (1)

Algoritam izvršavanja zadataka

Da bi se izvršila faktorizacija kvadratnih trinoma, morate znati Vitov teorem, imati rješenje pri ruci, moći pronaći grafički rješenje ili tražiti korijene jednadžbe drugog stupnja pomoću diskriminacijske formule. Ako je dan kvadratni trinomij i treba ga faktorizirati, slijed akcija je sljedeći:

1) Izjednačite izvorni izraz s nulom kako biste dobili jednadžbu.

2) Donesite takve uvjete (ako postoji takva potreba).

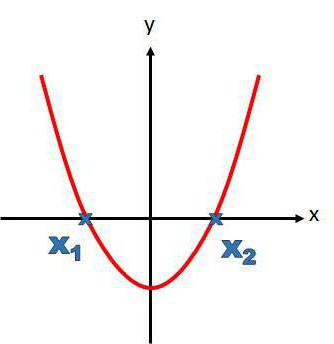
3) Pronađite korijene na bilo koji poznati način. Grafička metoda se najbolje koristi ako se unaprijed zna da su korijeni cijeli brojevi i mali brojevi. Treba zapamtiti da je broj korijena jednak maksimalnom stupnju jednadžbe, tj. kvadratna jednadžba dva korijena.

4) Zamijenite vrijednost x u izrazu (1).

5) Zapišite dekompoziciju kvadratnih faktora.

primjeri

Konačno shvatite kako se taj zadatak obavlja, dopušta praksu. Ilustrirajte faktoriranje kvadratnih primjera:

Potrebno je proširiti izraz:

x ² -17x = -32

Približimo se našem algoritmu:

1) x2 -17x + 32 = 0

2) smanjeni su slični izrazi

3) prema Viet formuli, teško je pronaći korijene za ovaj primjer, jer je bolje koristiti izraz za diskriminant:

D = 289-128 = 161 = (12,69) ²

x ₁ = 2,155

x2 = 14,845

4) Zamijenite korijene koje smo pronašli u osnovnoj formuli za razgradnju:

(x-2.155) _* (x-14.845)

5) Onda će odgovor biti:

x ² -17x + 32 = (x-2.155) (x-14.845)

Provjerite odgovaraju li rješenja pronađena diskriminantima Viet formulama:

2,155 + 14,845 = 17

14,845 ^. 2,155 = 32

Za te se korijene primjenjuje Viet-teorem, oni su ispravno pronađeni, što znači da je dobivena faktorizacija također ispravna.

Slično dekomponirati 12x2 + 7x-6.

12x2 + 7x-6 = 0

D = 337

x ₁ = -7 + (337) ^1/2

x ₂ = -7- (337) ^1/2

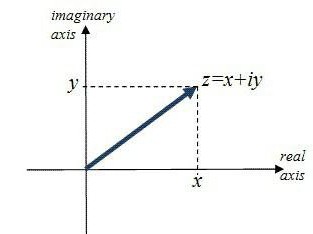
U prethodnom slučaju, rješenja su bila ne-cijeli, ali stvarni brojevi, koje je lako pronaći, s kalkulatorom ispred vas. Sada razmotrite složeniji primjer u kojem će korijeni biti složeni: faktoring x ² + 4x + 9. Prema formuli za Vieta, korijeni se ne mogu naći, a diskriminant je negativan. Korijeni će biti na složenoj ravnini.

D = -20

Polazeći od toga dobivamo zanimljive korijene -4 + 2i * 5 ^1/2 i -4-2i _* 5 ^1/2 , jer (-20) ^1/2 = 2i * 5 ^1/2 .

Dobivamo željenu razgradnju, zamjenjujući korijene u općoj formuli.

Drugi primjer: morate izraziti izraz 23x ² -14x + 7.

=0 Imamo jednadžbu 23x2 -14x + 7 = 0

D = -448

To znači da su korijeni 14 + 21,166i i 14-21,166i. Odgovor će biti:

23x2 -14x + 7 = 23 (x-14-21,166i) * (x-14 + 21, 166i).

Dajemo primjer, koji se može riješiti bez pomoći diskriminanta.

Pretpostavimo da je potrebno proširiti kvadratnu jednadžbu x 2 -32x + 255. Očito, može se riješiti diskriminantom, ali u ovom slučaju brže je pokupiti korijenje.

x 1 = 15

x 2 = 17

Dakle, x2 -32x + 255 = (x-15) (x-17).