Određivanje kutnog momenta, sile i inercije. Jednadžba trenutka Primjer rješavanja problema

Dinamika rotacije je jedan od važnih dijelova moderne mehanike, koji razmatra zakone rotacijskog kretanja tijela oko osi i točaka. U ovom članku detaljno ćemo proučiti glavnu jednadžbu dinamike rotacije - jednadžbu trenutka.

Trenutak impulsa

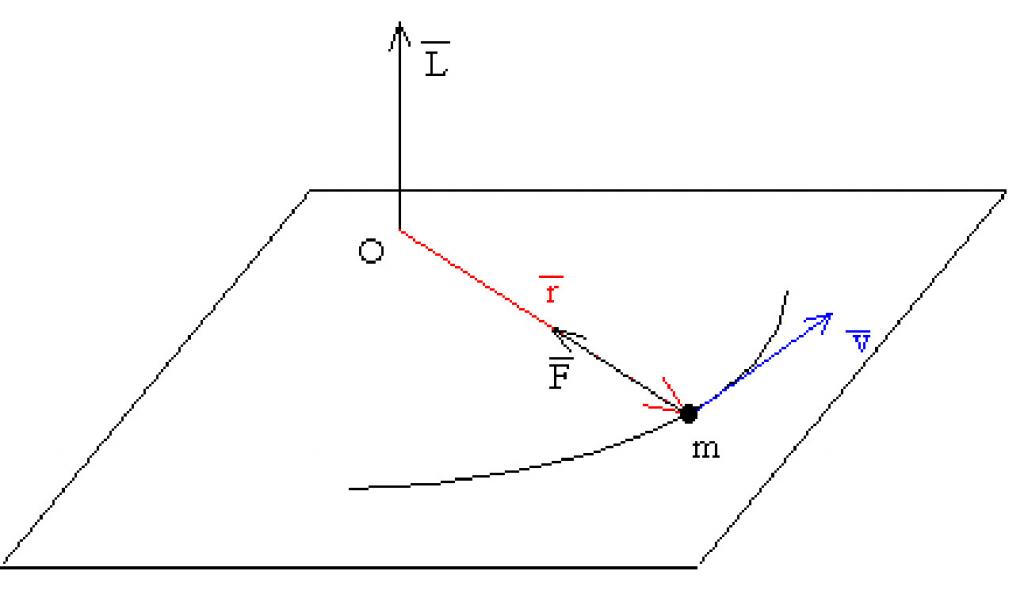
Svaka učenica zna što čini mehanički impuls, koji se ispravnije naziva količina pokreta. Pretpostavimo sada da se materijalna točka koja ima masu m okreće oko O-osi s linearnom brzinom v. Ako je radijus rotacije označen kao r, tada možemo napisati sljedeći izraz:

L¯ = [m * v¯ * r¯].

Prva dva faktora na desnoj strani jednakosti su linearni zamah točke. Produkt ovog impulsa vektorom rp, usmjeren od osi rotacije do točke, naziva se kutni moment L¯.

Vrijednost Lp je vektor. Usmjeren je okomito na ravninu rotacije točke. Smjer kutnog momenta materijalne točke određuje se pomoću pravila za desnu ruku ili pravila pravokutnika. Okretanje točke u smjeru suprotnom od kazaljke na satu stvara pozitivan kutni moment.

Budući da je brzina rotacije v¯ usmjerena tangencijalno na kružnu stazu, vektorski izraz može se prepisati u skalarnom obliku:

L = m * v * r.

Trenutak sile

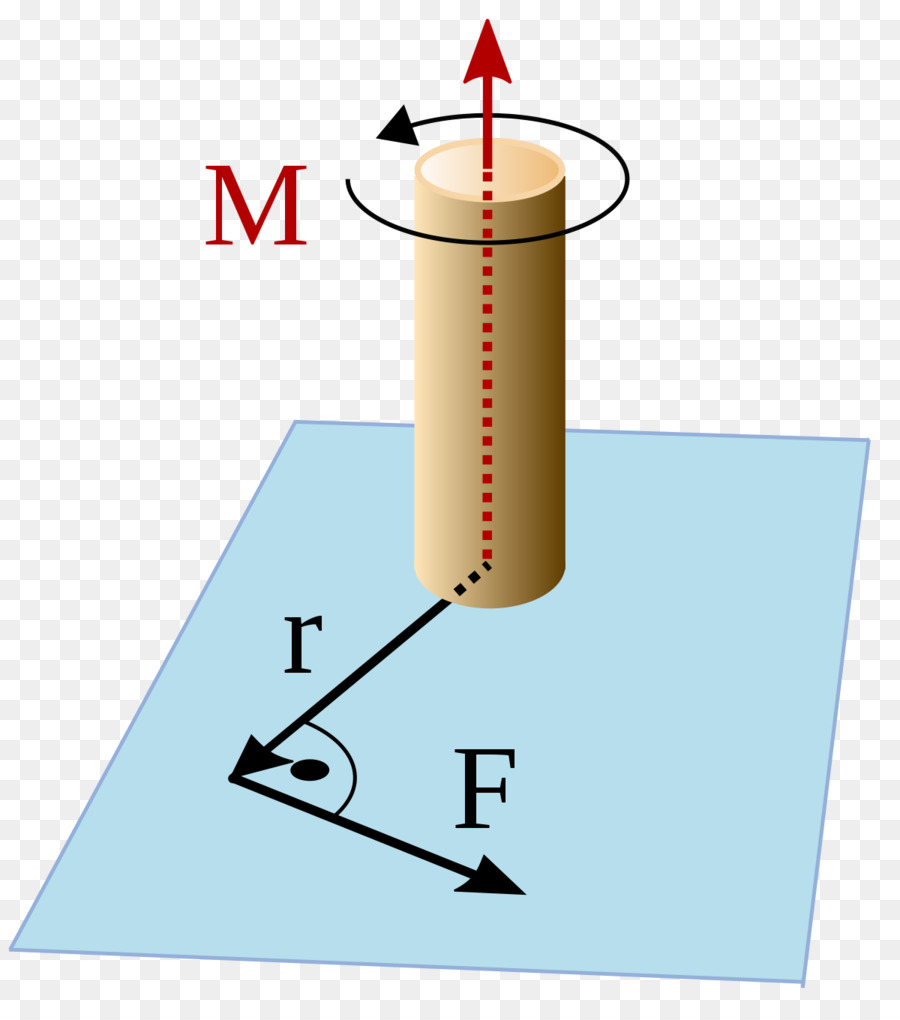
Ovo je još jedna važna značajka rotacijskog pokreta. U fizici se ta količina uvodi na isti način kao i kutni moment materijalne točke, ali umjesto količine gibanja, treba zamijeniti tangencijalnu silu u gornju formulu. Imamo:

M¯ = [r¯ * F¯].

Trenutak sile, koji se također naziva moment momenta, karakterizira sposobnost potonjeg da napravi zaokret sustava i da mu daje kutno ubrzanje.

Smjer vektora momenta M¯ određen je istim pravilima kao i za vektor L¯. Ako sustav izvodi ubrzanu rotaciju, onda M¯ i L¯ podudaraju u smjeru, ako se uspore, tada će biti suprotno usmjereni.

Ako su sila F ¯ i radijus-vektor r biti međusobno okomiti, tada će vektorski oblik zapisa postati sličan skalar:

M = r * F.

Vrijednost r naziva se poluga sile. Što je veća njegova vrijednost, to je veći trenutak kada sila F nastane, a veća će biti i kutna ubrzanja sustava.

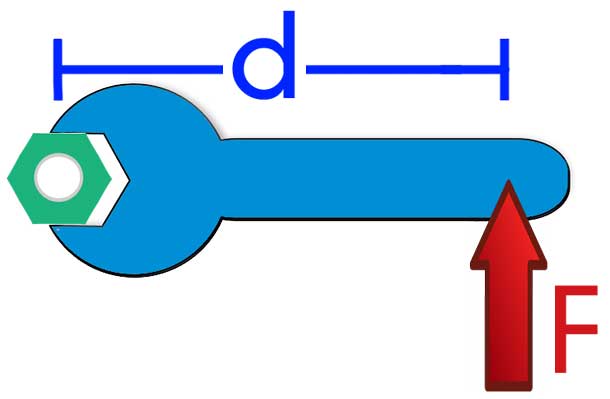
Primjeri koji bi omogućili jasniju predodžbu o tome što je fizičko značenje Mpi, odvijaju maticu posebnim dugačkim ključem, procesom otvaranja vrata s njegovim guranjem blizu ručke i blizu šarki vrata, kao i procesom držanja tijela određene mase na rastegnutom i pritisnutom tijelu ruka.

Trenutak inercije

Ostaje definirati treću točku, koja se koristi za kvantitativno opisivanje procesa rotacije. Trenutak inercije materijalne točke, čiji su parametri zabilježeni na početku članka, izračunava se po formuli:

I = m * r2.

Za razliku od druga dva momenta (M¯ i L¯), trenutak inercije je skalar. Pomoću njega opisuju se inercijalna svojstva sustava (analogija s masom tijekom translacijskog gibanja).

Očito, da biste odredili vrijednost I za čvrsto tijelo složenog oblika i nejednoliku gustoću, trebate koristiti integralni broj:

I = ( _m (r2 * dm).

Zapravo, formula odražava zbroj količina _i za svaku materijalnu točku i.

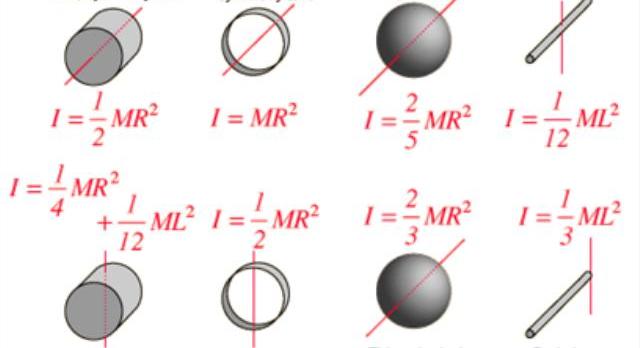
Trenutak inercije I karakterističan je ne samo za oblik i raspodjelu mase u sustavu rotacije, već ovisi io položaju osi. Na primjer, mnogi su primijetili da je mnogo lakše rotirati metalnu šipku ili drvenu mopu duž osi koja prolazi kroz njihovu dužinu nego duž okomice. U drugom slučaju, moment inercije poprima veći značaj.

Jednadžba trenutka za materijalnu točku

Sada je vrijeme da krenete izravno na temu članka. Ako zakretni moment M djeluje za vrijeme dt, onda to dovodi do promjene kutnog momenta za iznos dL, odnosno:

dL = M * dt.

Ta jednakost je diferencijalni oblik pisanja jednadžbe trenutka u fizici. Prenesite pojam dt na lijevu stranu jednakosti i ponovno napišite dL eksplicitno, dobivamo:

dL / dt = M =>

m * dv * r / dt = M.

Podsjetimo se da je linearna brzina u kinematici povezana s slijedećom jednadžbom:

v = ω * r.

Zamjenjujući ga u jednadžbu trenutaka, dobivamo:

m * dω * r2 / dt = M =>

I * α = M, gdje je α = dω / dt, I = m * r2.

Dobivena jednakost često se koristi za određivanje kinematičkih značajki rotirajućeg sustava ako su poznati momenti vanjskih sila M i moment inercije I.

Zakon očuvanja vrijednosti L

Jednadžba trenutka pokazuje kako se kutni moment mijenja ako djeluje vanjski trenutak M. Što će se dogoditi sustavu ako M ispadne nula? U tom će slučaju vrijednost L biti spremljena. Matematička formula za ovu situaciju je napisana kako slijedi:

L = const ili

L = m * r * v = m * r ² * ω = I * ω = const.

Treba napomenuti da uvjet M = 0 treba zadovoljavati samo za vanjske sile. Unutarnje sile koje stvaraju trenutak M ne mogu promijeniti trenutak zamaha sustava.

Zakon o zaštiti L koristi se za rotiranje umjetnih satelita u svemiru i na klizanju. Dakle, grupirajući se na različite načine, sportaš mijenja vrijednost svog momenta inercije, što dovodi do proporcionalne promjene brzine njegove kutne rotacije.

Primjer zadatka

Na materijalnu točku od 2 kg djeluje sila od 10 N, znajući da je polumjer rotacije materijalne točke oko osi 0,5 m, a također s obzirom da sila djeluje tangencijalno na putanju, potrebno je utvrditi kutnu brzinu točke 5 sekundi nakon početka kretanja ,

Pišemo jednadžbu trenutka i izrazimo ubrzanje α:

I * α = M =>

α = M / I.

Sada zamjenjujemo izraze za M i I, uzimajući u obzir uvjete problema, imamo:

α = F * r / (m * r ² ) = F / (m * r).

Budući da se kretanje koje se razmatra događa s konstantnim ubrzanjem α, sljedeća formula će biti prikladna za izračunavanje:

ω = α * t.

Zamjenjujući u njoj dobiveni izraz za α, dolazimo do konačne radne formule:

ω = F * t / (m * r).

S obzirom na podatke problema, možete napisati odgovor: ω = 50 rad / s. Ova vrijednost odgovara gotovo 8 punih okretaja oko osi u sekundi.