Kako pronaći područje poligona?

U problemima geometrije često je potrebno izračunati površinu poligona. Štoviše, može imati prilično raznolik oblik - od poznatog trokuta do određenog n-kuta s nekim nezamislivim brojem vrhova. Osim toga, ovi poligoni su konveksni ili konkavni. U svakoj situaciji treba graditi na izgledu figure. Tako se ispostavilo da odaberete najbolji način za rješavanje problema. Oblik može biti točan, što će znatno pojednostaviti rješenje problema.

Malo teorije poligona

Ako su nacrtane tri ili više ravnih linija koje se sijeku, one tvore određeni lik. Da je poligon. Po broju točaka presijecanja postaje jasno koliko će to vrhova imati. Oni daju ime dobivene figure. To može biti:

• trokut;
• četverokut;
• penta ili šesterokut i tako dalje.

Takav će podatak zasigurno obilježiti dvije odredbe:

1. Susjedne strane ne pripadaju jednoj pravoj liniji.
2. Ne-susjedne točke nemaju zajedničkih točaka, tj. Ne sijeku se.

Da biste razumjeli koji su vrhovi susjedni, morate vidjeti pripadaju li oni istoj strani. Ako je tako, sljedeći. Inače se mogu povezati segmentom, koji se naziva dijagonalom. Mogu se crtati samo u poligonima koji imaju više od tri vrha.

Koje su njihove vrste?

Poligon s više od četiri ugla može biti konveksan ili konkavan. Razlika ovog potonjeg je u tome što neki od njegovih vrhova mogu ležati na suprotnim stranama ravne crte nacrtane kroz proizvoljnu stranu poligona. U konveksnom, svi vrhovi uvijek leže na jednoj strani takve linije.

U školskom tijeku geometrije najveći dio vremena dobiva se točno konveksnim likovima. Stoga je u problemima potrebno pronaći područje konveksnog poligona. Zatim slijedi formula kroz radijus opisne kružnice, koja vam omogućuje da pronađete željenu vrijednost za bilo koji oblik. U drugim slučajevima, jedinstveno rješenje ne postoji. Za trokut, formula je jedna, a za kvadrat ili trapez potpuno drugačiji. U situacijama kada je oblik nepravilan ili ima mnogo vrhova, uobičajeno je da se dijele na jednostavne i poznate.

Što učiniti ako komad ima tri ili četiri vrha?

U prvom slučaju to će biti trokut, a možete koristiti jednu od formula:

• S = 1/2 * a * n, gdje je a strana, n je visina;
• S = 1/2 * a * b * sin (A), gdje su a i b strane trokuta, A je kut između poznatih strana;
• S = √ (p * (p - a) * (p - c) * (p - c)), gdje je c strana trokuta, do već označene dvije, p je polu - perimeter, odnosno zbroj sve tri strane, podijeljen u dva. ,

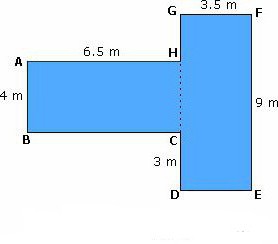
Slika s četiri vrha može biti paralelogram:

• S = a * n;
• S = 1/2 * d ₁ * d ₂ * sin (α), gdje su d ₁ i d ₂ dijagonale, α je kut između njih;
• S = a * u * sin (α).

Formula za trapezna područja: S = n * (a + b) / 2, gdje su a i b duljine baza.

Što učiniti s pravilnim poligonom s više od četiri vrha?

Za početak, takvu osobinu karakterizira činjenica da su u njoj sve strane jednake. Osim toga, poligon ima iste kutove.

Ako je oko takve figure opisan krug, njegov će se radijus podudarati s segmentom od središta poligona do jednog od vrhova. Stoga, da bismo izračunali površinu regularnog poligona s proizvoljnim brojem vrhova, trebamo sljedeću formulu:

S _n = 1/2 * n * R _n ² * sin (360º / n), gdje je n broj vrhova poligona.

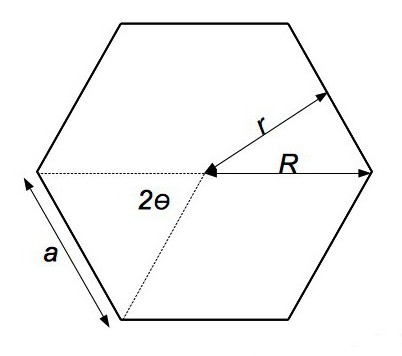
Iz njega je lako dobiti onaj koji je koristan za posebne slučajeve:

1. trokutići: S = (3'3) / 4 * R2;
2. kvadrat: S = 2 * R2;
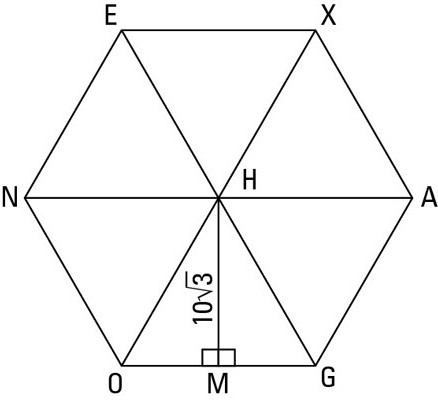
3. šesterokut: S = (3√3) / 2 * R2.

Situacija s pogrešnom figurom

Algoritam je način pronalaženja područja poligona, ako nije točan i ne može se pripisati nekoj od poznatih figura:

• razlomite ga u jednostavne oblike, kao što su trokuti, tako da se ne sijeku;
• izračunajte njihovo područje pomoću bilo koje formule;
• zbrojite sve rezultate.

Što učiniti ako su koordinate točaka poligona dane u problemu?

To znači da je skup parova brojeva za svaku točku poznat kao ograničenje strana figure. Obično se pišu kao (x ₁ ; y ₁ ) za prvi, (x ₂ ; y ₂ ) za drugi, a n-ti vrh ima te vrijednosti (x _n ; y _n ). Tada se područje poligona definira kao zbroj n pojmova. Svaki od njih izgleda ovako: ((y _{i + 1} + y _i ) / 2) * (x _{i + 1} - x _i ). U ovom izrazu, i varira od jednog do n.

Treba napomenuti da će znak rezultata ovisiti o izbjegavanju oblika. Kada koristite navedenu formulu i krećete se u smjeru kazaljke na satu, odgovor će biti negativan.

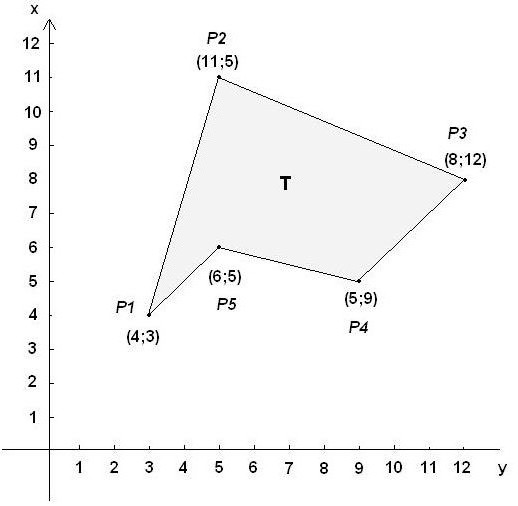
Primjer zadatka

Stanje. Koordinate vrhova dane su vrijednostima (0,6; 2,1), (1,8; 3,6); (2,2; 2,3); (3,6; 2,4); (3,1; 0,5). Za izračun površine poligona.

Odluka. Prema gornjoj formuli prvi će izraz biti (1,8 + 0,6) / 2 * (3,6 - 2,1). Ovdje samo trebate uzeti vrijednosti za igru ​​i X iz drugog i prvog boda. Jednostavan izračun će dovesti do rezultata 1.8.

Na sličan način dobiva se i drugi pojam: (2.2 + 1.8) / 2 * (2.3 - 3.6) = -2.6. Pri rješavanju takvih problema nemojte se bojati negativnih vrijednosti. Sve ide kako treba. To je planirano.

Isto tako, dobivene su vrijednosti za treći (0,29), četvrti (-6.365) i peti (2.96). Tada je ukupna površina: 1,8 + (-2,6) + 0,29 + (-6,365) + 2,96 = - 3,915.

Savjet za rješavanje problema za koji je poligon prikazan na papiru u ćeliji

Najčešće je zbunjujuće da je u podacima prisutna samo veličina ćelija. No, ispada da više informacija nije potrebno. Preporuka za rješavanje ovog problema je podjela oblika na mnogo trokuta i pravokutnika. Njihovo područje je prilično jednostavno brojiti duljinu zabava, koje se tada lako savijaju.

No, često postoji jednostavniji pristup. Sastoji se od crtanja figure u pravokutnik i izračunavanja vrijednosti njegovog područja. Zatim prebrojite područja onih elemenata koji su suvišni. Oduzmite ih od ukupnog iznosa. Ova opcija ponekad uključuje nešto manji broj radnji.