Rotacijsko gibanje i kutna brzina krutine

U ovom članku raspravit ćemo o fizikalnim veličinama koje karakteriziraju rotacijsko gibanje tijela: kutnu brzinu, kutni pomak, kutno ubrzanje i moment sila.

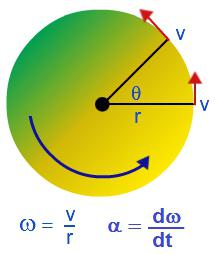
Kruto tijelo je skup kruto povezanih materijalnih točaka. Kada se čvrsto tijelo vrti oko bilo koje osi, pojedinačne materijalne točke iz kojih se dodaje kreću se po krugovima različitih radijusa.

U određenom vremenskom razdoblju, na primjer, tijekom kojeg tijelo proizvodi jednu revoluciju, odvojene materijalne točke koje sačinjavaju čvrsto tijelo, prolazit će različitim putevima, stoga će odvojene točke imati različite linearne brzine. Opisati rotaciju krutine pomoću linearnih brzina pojedinca materijalne točke - teško.

Kutni pomak

Međutim, analizirajući kretanje pojedinih materijalnih točaka, može se utvrditi da se u istom vremenskom razdoblju svi okreću oko osi pod istim kutom. To jest, da bi se opisala rotacija krutine, prikladno je upotrijebiti takvu fizičku veličinu kao kutni pomak:

φ = φ (t).

Kutna brzina i kutno ubrzanje

Rotacijsko gibanje može se karakterizirati kutnom brzinom: ω = ∆ / ∆t.

Kutna brzina karakterizira brzinu rotacije tijela i jednaka je omjeru promjene zakretnog kuta prema vremenu u kojem je došlo do promjene. Mjereno u radijanima u sekundi: [ω] = rad / s.

Kutna brzina rotacije povezana je s linearnom brzinom slijedećim odnosom: v = Rω, gdje je R polumjer kruga uz koji se tijelo kreće.

Rotacijski pokret tijelo karakterizira još jedna fizikalna veličina - kutno ubrzanje, koje je jednako omjeru promjene kutne brzine i vremena tijekom kojeg je došlo do toga: ε = /ω / .t. Jedinica za mjerenje kutnog ubrzanja: [ε] = rad / s ² .

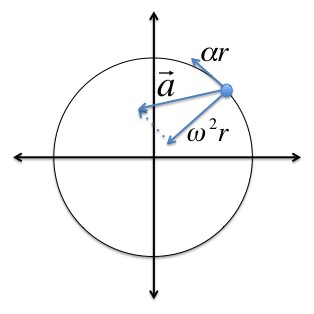
Kutna brzina i kutno ubrzanje su pseudovektori čiji smjer ovisi o smjeru vrtnje. Može se odrediti pravilom desnog vijka.

Ravnomjerno rotacijsko gibanje

Ujednačeno rotacijsko kretanje provodi se s konstantnom kutnom brzinom i opisuje se sljedećim jednadžbama: ε = 0, ω = const, φ = + ₀ + ωt, gdje je is ₀ početna vrijednost zakretnog kuta.

Ravnomjerno ubrzano rotacijsko gibanje

Ravnomjerno ubrzano rotacijsko kretanje događa se s konstantnim kutnim ubrzanjem i opisuje se sljedećim jednadžbama: ε = const, ω = ω ₀ + εt, φ = + ₀ + ω ₀ t + εt 2/2.

Tijekom rotacije krutine centripetalno ubrzanje svaka se točka ovog tijela može pronaći na sljedeći način:. _c = v ² / R = (ωR) ² / R = ω ² R.

Kada se rotacija krutine ubrza, tangencijalno ubrzanje njezinih točaka može se pronaći pomoću formule: _t = /V / =t = ∆ (ωR) / =t = R (/ω / )t) = Rε.

Trenutak snage

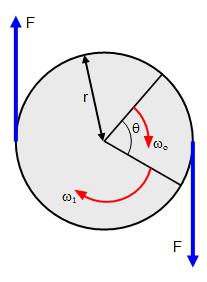
Ako se, s obzirom na fizički problem, ne bavimo materijalnom točkom, već čvrstim tijelom, tada se djelovanje više sila na njega primjenjuje na različite točke ovog tijela ne može se svesti na djelovanje jedne sile. U ovom slučaju razmotrite trenutak sila.

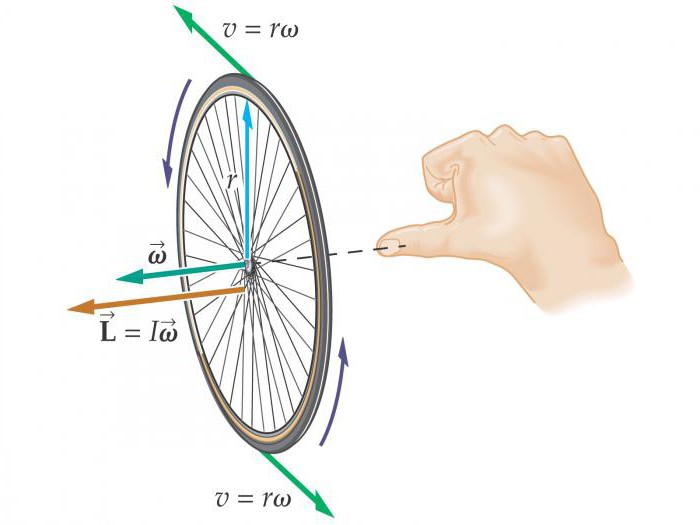
Trenutak sile naziva se proizvodom sile na ramenu. To je vektorska veličina, a nalazi se po formuli: M = RFsinα, gdje je α kut između vektora R i F. Ako postoji nekoliko trenutaka sila koje djeluju na tijelo, tada se njihovo djelovanje može zamijeniti njihovim rezultantnim, vektorskim zbrojem tih trenutaka: M = M ₁ + M ₂ + ... + M _n .

Eksperimenti i iskustva pokazuju da se pod djelovanjem trenutka sile mijenja kutna brzina tijela, tj. Tijelo ima kutno ubrzanje. Utvrdimo kako kutno ubrzanje materijalne točke (skup materijalnih točaka) ovisi o primijenjenom momentu: F = mɑ, RF = Rma = R ² mβ, β = M / mR ² = M / I, gdje je I = mR ² trenutak inercije materijala točka. Imajte na umu da trenutak inercije tijela ovisi o masi tijela i o položaju te mase u odnosu na os rotacije.

Primjeri rješavanja problema

Zadatak 1. Rotor centrifuge čini 2 • 10 ⁴ o / min. Nakon što se motor isključi, njegova rotacija se zaustavlja nakon 8 minuta. Prona ite kutno ubrzanje, kao i broj okretaja koje rotor čini od trenutka kada se motor isključi dok se ne zaustavi, s obzirom da se kretanje rotora jednoliko ubrzava.

odluka

Nađimo kutno ubrzanje, uzimajući u obzir da se kutna brzina s jednoliko ubrzanim gibanjem opisuje jednadžbom: ω (t) = ω ₀ - εt.

Dakle, s obzirom da je na kraju gibanja brzina jednaka nuli, nalazimo: ε = ω ₀ / t = 2πn / t.

Prenošenjem tih zadataka na SI jedinicu jedinica (n = 333 o / s; t = 480 s) dobivamo: ε = 2π333 / 480 = 4.36 (rad / s ² ).

Kut rotacije rotora centrifuge tijekom vremena t bit će: t (t) = + ₀ + ω ₀ t + εt 2/2. Čitajući izraz za kutno ubrzanje i činjenicu da je = ₀ = 0 , nalazimo: φ (t) = ω ₀ t / 2 = πnt.

Broj obrtaja rotora za to vrijeme bit će: N = t (t) / 2π = πnt / 2π = nt = 8 • 10 ⁴ (vol.).

Odgovor: kutno ubrzanje iznosi 4,36 rad / s ² ; broj okretaja koje je napravio rotor od trenutka isključenja motora do potpunog zaustavljanja iznosi 8 • 10 ⁴ o / min.

Zadatak 2. Disk koji ima masu od 1 kg i polumjer od 20 cm rotira s frekvencijom od 120 o / min. za minutu. Pod djelovanjem kočnice uređaj na rubu diska počeo djelovati sila trenja 10 N. Nađite vrijeme za zaustavljanje diska, nakon što počne djelovati sila trenja.

odluka

Pronađite kočni moment koji djeluje na disk: M = RF.

Nađite kutno ubrzanje diska: ε = M / I = FR / mR ² = F / mR.

Nađimo vrijeme za koje će se disk zaustaviti: t = ω ₀ / ε , gdje je ω ₀ početna kutna brzina diska, koja je jednaka 2πv.

Izračunavamo: t = 2πv / ε = 2πvmR / F = 6,28 • 2 • 1 • 0,2 / 10 = 2,5 (s).

Odgovor: vrijeme zaustavljanja je 2,5 sekunde.