Neke točke o načinu rješavanja nejednakosti
Jedna od tema koja zahtijeva maksimalnu pažnju i ustrajnost učenika je rješavanje nejednakosti. Takve slične jednadžbe i u isto vrijeme vrlo različite od njih. Zato što njihovo rješenje zahtijeva poseban pristup.
Svojstva koja će biti potrebna za pronalaženje odgovora
Svi se oni koriste za zamjenu postojećeg zapisa ekvivalentom. Većina njih je slična onoj u jednadžbama. Ali postoje razlike.
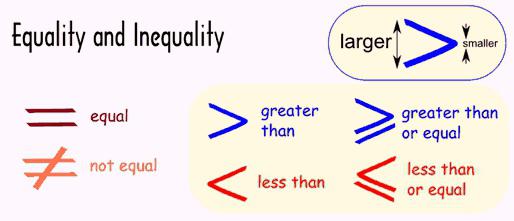
- Funkcija koja je definirana u LDU ili bilo koji broj može se dodati na obje strane izvorne nejednakosti.
- Slično tome, množenje je moguće, ali samo pozitivnom funkcijom ili brojem.
- Ako se ova radnja izvodi s negativnom funkcijom ili brojem, tada se znak nejednakosti mora zamijeniti suprotnim.
- Funkcije koje nisu negativne mogu se podići na pozitivnu snagu.
Ponekad je rješavanje nejednakosti popraćeno akcijama koje daju vanjske odgovore. Potrebno ih je eliminirati usporedbom domene DHS-a i raznih rješenja.
Korištenje metode razmaka
Njezina je bit svoditi nejednakost na jednadžbu, u kojoj je na desnoj strani nula.
- Odredite područje na kojem se nalaze valjane vrijednosti varijabli, tj. LDL.
- Preobrazite nejednakost pomoću matematičkih operacija tako da se u desnom dijelu nalazi nula.
- Zamijenite znak nejednakosti s "=" i riješite odgovarajuću jednadžbu.
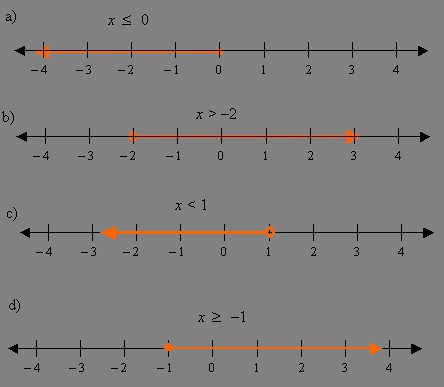
- Na numeričkoj osi označite sve odgovore koji su se pojavili tijekom rješavanja, kao i intervale TLD. Uz strogu nejednakost točke koju trebate nacrtati probušene. Ako postoji znak jednakosti, onda bi trebali slikati.
- Odredite znak izvorne funkcije na svakom intervalu koji proizlazi iz točaka LDD-a i podijelite njegove odgovore. Ako se na prijelazu kroz točku znak funkcije ne promijeni, on ulazi u odgovor. Inače - isključeni.
- Granične točke za TLD potrebno je dodatno provjeriti i tek onda uključiti ili ne u odgovor.
- Odgovor koji se dobije mora biti napisan u obliku ujedinjenih skupova.
Malo o dvostrukim nejednakostima
Oni koriste dva znaka nejednakosti u zapisu. To znači da je neka funkcija ograničena uvjetima dva puta. Takve se nejednakosti rješavaju, kao sustav od dva, kada je izvornik podijeljen na dijelove. U intervalnoj metodi prikazani su odgovori iz rješenja obje jednadžbe.
Za njihovo rješavanje također je dopušteno koristiti gore navedena svojstva. Uz njihovu pomoć prikladno je smanjiti nejednakost na jednakost nula.

Kakva je situacija s nejednakostima u kojima postoji modul?
U ovom slučaju, rješenje nejednakosti koristi sljedeća svojstva i istinita su za pozitivnu vrijednost "a".
Ako "x" uzima algebarski izraz, onda su takve zamjene istinite:
- | x | <a do -a <x <a;
- | x | > a na x <-a ili x> a.
Ako nejednakosti nisu striktne, tada su i formule istinite, samo se u njima, osim više ili manje znaka, pojavljuje "=".
Kako riješiti sustav nejednakosti?
To znanje će biti potrebno u slučajevima kada je takav zadatak dan ili postoji zapis dvostruke nejednakosti ili se modul pojavljuje u zapisu. U takvoj situaciji, rješenje bi bile vrijednosti varijabli koje bi zadovoljile sve nejednakosti u zapisu. Ako nema takvih brojeva, sustav nema rješenja.
Plan rješavanja sustava nejednakosti:
- riješiti svaku od njih posebno;
- nacrtati sve intervale na numeričkoj osi i odrediti njihova sjecišta;
- napišite odgovor sustava, koji će biti spoj onoga što se dogodilo u drugom paragrafu.
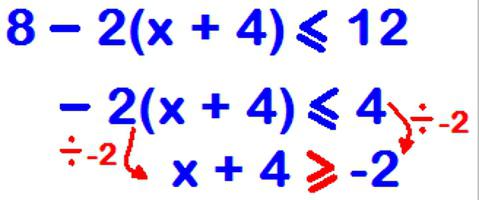
Kako se nositi s djelomičnim nejednakostima?
Budući da je tijekom njihovog rješavanja možda potrebno promijeniti znak nejednakosti, potrebno je pažljivo i pažljivo provesti sve točke plana. U suprotnom, to bi mogao biti suprotan odgovor.
Rješavanje frakcijskih nejednakosti također koristi intervalnu metodu. A akcijski plan će biti:
- Koristeći opisana svojstva, dajte frakciji takav izgled da ostaje samo nula desno od znaka.
- Zamijenite nejednakost s "=" i odredite točke na kojima će funkcija biti jednaka nuli.
- Označite ih na osi koordinata. U tom slučaju, brojevi koji su rezultat izračuna u nazivniku uvijek će biti probušeni. Svi ostali - na temelju uvjeta nejednakosti.
- Odredite intervale konzistentnosti.
- U odgovoru napišite uniju tih intervala, čiji znak odgovara onome što je bilo u izvornoj nejednakosti.
Situacije u kojima se iracionalnost pojavljuje u nejednakosti
Drugim riječima, u zapisu postoji matematički korijen. Budući da se u školskom tečaju algebre najviše bavi zadacima kvadratni korijen onda će se razmotriti.
Rješenje iracionalnih nejednakosti jest dobivanje sustava od dva ili tri, što će biti ekvivalentno izvorniku.
| Izvorna nejednakost | stanje | ekvivalentni sustav |
| (N (x) <m (x) | m (x) je manji ili jednak 0 | nema rješenja |
| m (x) veći od 0 | n (x) je veći ili jednak 0 n (x) <(m (x)) 2 | |
| (N (x)> m (x) | m (x) je veći ili jednak 0 n (x)> (m (x)) 2 | |
ili n (x) je veći ili jednak 0 m (x) je manje od 0 | ||
| (N (x) ≤ m (x) | m (x) je manje od 0 | nema rješenja |
| m (x) je veći ili jednak 0 | n (x) je veći ili jednak 0 n (x) ≤ (m (x)) 2 | |
| (N (x) ≥ m (x) | m (x) je veći ili jednak 0 n (x) ≥ (m (x)) 2 | |
ili n (x) je veći ili jednak 0 m (x) je manje od 0 | ||
| (N (x) <(m (x) | n (x) je veći ili jednak 0 n (x) je manja od m (x) | |
| (N (x) * m (x) <0 | n (x) je veći od 0 m (x) je manje od 0 | |
| (N (x) * m (x)> 0 | n (x) je veći od 0 m (x) veći od 0 | |
| (N (x) * m (x) ≤ 0 | n (x) je veći od 0 m (x) ≤0 | |
ili n (x) je 0 m (x) - bilo koji | ||
| (N (x) * m (x) ≥ 0 | n (x) je veći od 0 m (x)> 0 | |
ili n (x) je 0 m (x) - bilo koji |
Primjeri rješavanja različitih vrsta nejednakosti
Da bismo dodali jasnoću teoriji rješavanja nejednakosti, u nastavku su primjeri.
Prvi primjer. 2x - 4> 1 + x
Rješenje: kako bi se odredio TLD, dovoljno je samo pomno pogledati nejednakost. Formira se iz linearnih funkcija, stoga je definirana za sve vrijednosti varijable.
Sada s obje strane nejednakosti treba oduzeti (1 + x). Ispada: 2x - 4 - (1 + x)> 0. Nakon što su zagrade otvorene i dani takvi izrazi, nejednakost poprima sljedeći oblik: x - 5> 0.
Izjednačavajući ga s nulom, lako je pronaći njezino rješenje: x = 5.
Sada ovu točku s brojem 5, trebate označiti na koordinatnom snopu. Zatim provjerite znakove izvorne funkcije. U prvom intervalu od minus beskonačnosti do 5 možete uzeti broj 0 i zamijeniti ga nejednakostima koje su rezultat transformacija. Nakon izračuna, ispalo je -7> 0. ispod luka intervala morate potpisati znak minus.
Na sljedećem intervalu od 5 do beskonačnosti možete odabrati broj 6. Onda se ispostavi da je 1> 0. Pod lukom je potpisan znak “+”. Ovaj drugi interval će biti odgovor na nejednakost.
Odgovor: x leži u intervalu (5; ∞).
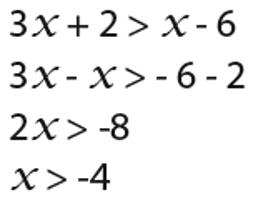
Drugi primjer. Potrebno je riješiti sustav od dvije jednadžbe: 3x + 3 ≤ 2x + 1 i 3x - 2 ≤ 4x + 2.
Odluka. LDL tih nejednakosti također leži u domeni bilo kojeg broja, budući da su dane linearne funkcije.
Onda morate djelovati u fazama. Prvo pretvorite prvu od nejednakosti i izjednačite je s nulom. 3x + 3 - 2x - 1 = 0. To jest, x + 2 = 0. Dakle, x je -2.
Druga će se nejednakost pojaviti u obliku takve jednadžbe: 3x - 2 - 4x - 2 = 0. Nakon transformacije: - x - 4 = 0. Ona daje vrijednost za varijablu jednaku -4.
Ta dva broja trebaju biti označena na osi, prikazujući intervale. Budući da nejednakost nije stroga, sve točke moraju biti obojane. Prvi interval od minus beskonačnosti do -4. Neka broj bude -5. Prva nejednakost će dati vrijednost -3, a druga ne, što znači da se ta razlika ne nalazi u odgovoru.
Drugi interval je od -4 do -2. Možete odabrati broj -3 i zamijeniti ga u obje nejednakosti. U prvom i drugom dobiva se vrijednost -1. Dakle, pod lukom "-".
Na zadnjem intervalu od -2 do beskonačnosti, najbolji broj je nula. Potrebno ga je nadomjestiti i pronaći vrijednosti nejednakosti. U prvom se dobiva pozitivan broj, a drugi je nula. Taj se jaz također treba isključiti iz odgovora.
Od tri intervala, rješenje nejednakosti je samo jedno.
Odgovor: x pripada [-4; -2].

Treći primjer. | 1 - x | > 2 | x - 1 |
Odluka. Prvi korak je odrediti točke na kojima funkcije nestaju. Za lijevo ovaj broj će biti 2, za desnu - 1. treba ih označiti na zraku i odrediti intervale znaka postojanosti.
U prvom intervalu, od minus beskonačnosti do 1, funkcija s lijeve strane nejednakosti uzima pozitivne vrijednosti, a s desne strane negativne vrijednosti. Pod lukom, morate upisati dva znaka "+" i "-" jedan uz drugi.
Sljedeći interval je od 1 do 2. Na njemu obje funkcije dobivaju pozitivne vrijednosti. Dakle, pod lukom, dva plus.
Treći interval od 2 do beskonačnosti daje sljedeći rezultat: lijeva funkcija je negativna, desna pozitivna.
Uzimajući u obzir dobivene znakove, potrebno je izračunati vrijednosti nejednakosti za sve intervale.
Na prvom mjestu dobivamo sljedeću nejednakost: 2 - x> - 2 (x - 1). Minus prije dva u drugoj nejednakosti posljedica je činjenice da je ova funkcija negativna.
Nakon transformacije, nejednakost izgleda ovako: x> 0. Ona odmah daje vrijednosti varijable. To znači da se iz tog intervala vraća samo interval od 0 do 1.
Na drugom: 2 - x> 2 (x - 1). Konverzije će dati sljedeću nejednakost: -3x + 4 više od nule. Njegova nula je x = 4/3. Uzimajući u obzir znak nejednakosti, ispada da x mora biti manji od tog broja. Stoga se taj interval svodi na interval od 1 do 4/3.
Ovo potonje daje sljedeću evidenciju nejednakosti: - (2 - x)> 2 (x - 1). Njegova transformacija dovodi do sljedećeg: x> 0. To jest, jednadžba je istinita za x manje od nule. To znači da u traženoj praznini nejednakost ne daje rješenja.
U prva dva intervala granica se pokazala kao broj 1. Potrebno ju je zasebno provjeriti. To jest, zamjena izvorne nejednakosti. Ispada: | 2 - 1 | > 2 | 1 - 1 | Izračun daje da je 1 veći od 0. Ovo je valjana izjava, tako da je jedna uključena u odgovor.
Odgovor: x leži u intervalu (0; 4/3).