Simetrala trokuta - što je to?

Geometrija je jedna od najsloženijih i zamršenih znanosti. U njoj se ono što se na prvi pogled čini očigledno vrlo rijetko ispostavlja ispravnim. Simptomi, visine, medijani, projekcije, tangente su ogroman broj stvarno teških pojmova s ​​kojima se vrlo lako može zbuniti.

Zapravo, uz pravilnu želju, možete razumjeti teoriju bilo koje složenosti. Kada je riječ o simetrali, medijani i visini, morate shvatiti da oni nisu svojstveni trokutima. Na prvi pogled, to su jednostavne linije, ali svaka od njih ima svoja svojstva i funkcije, čije poznavanje uvelike pojednostavljuje rješavanje geometrijskih problema. Dakle, što je simetrala trokuta?

definicija

Izraz "simetrala" dolazi od kombinacije latinskih riječi "dva" i "rez", "rez", što indirektno ukazuje na njegova svojstva. Obično, kada se djeca upoznaju s ovim snopom, od njih se traži da zapamte kratku frazu: "Simetrala je štakor koji trči u kutovima i prepolovi kut". Naravno, takvo objašnjenje nije prikladno za starije učenike, osim što se obično ne pitaju o ugljenu, nego o geometrijski oblik. Tako simetrala trokuta je zraka koja povezuje vrh trokuta s suprotnom stranom, a kut dijeli na dva jednaka dijela. Točka suprotne strane, na koju dolazi simetrala, za proizvoljni trokut odabire se nasumično.

Osnovne funkcije i svojstva

Glavna svojstva ove zrake malo. Prvo, jer simetrala trokuta dijeli kut na pola, svaka točka koja leži na njoj bit će na jednakoj udaljenosti od strana koje tvore vrh. Drugo, u svakom trokutu mogu se nacrtati tri bisektrike, prema broju dostupnih kuteva (stoga će ih već biti četiri u istom četverokutu i tako dalje). Točka u kojoj se sva tri zraka sijeku je središte kružnice upisane u trokut.

Svojstva su komplicirana

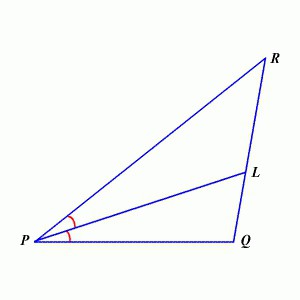
Malo ćemo komplicirati teoriju. Još jedno zanimljivo svojstvo: simetrala kuta trokuta dijeli suprotnu stranu na segmente čiji je omjer jednak omjeru stranica koje tvore vrh. Na prvi pogled, to je teško, ali zapravo je sve jednostavno: u predloženoj slici, RL: LQ = PR: PK. Usput, ovo svojstvo je nazvano teorem o Bisectrix i prvi put se pojavio u djelima starogrčkog matematičara Euclida. Zapamtili su je u jednom od ruskih udžbenika tek u prvoj četvrtini sedamnaestog stoljeća.

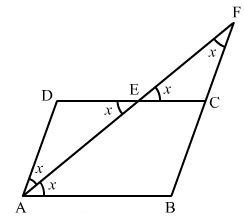
Malo teže. U četverokutnici simetrala presijeca jednakokračan trokut. Ova slika prikazuje sve jednake kutove za srednji AF.

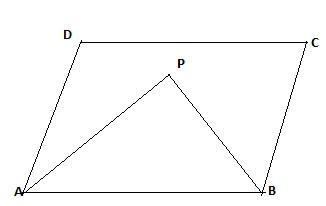
Štoviše, u četverokutima i trapezima, simetrale jednolikih kutova su okomite jedna na drugu. Na crtežu je kut APB-a 90 stupnjeva.

U jednakokračnom trokutu

Jednakokraki jednakokračan trokut je mnogo korisnija zraka. To je ujedno ne samo djelitelj ugla na pola, nego i medijan i visina.

Medijan je segment koji izlazi iz određenog kuta i pada na sredinu suprotne strane, dijeleći ga na jednake dijelove. Visina je okomica koja je pala s vrha na suprotnu stranu, s njezinom pomoći svaki se zadatak može svesti na jednostavni i primitivni Pitagorin teorem. U takvoj situaciji simetrala trokuta jednaka je korijenu razlike između kvadrata hipotenuze i druge noge. Usput, upravo je to svojstvo najčešće u geometrijskim problemima.

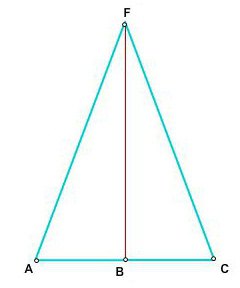
Popraviti: u ovom trokutu, simetrala FB je medijan (AB = BC) i visina (kutovi FBC i FBA su 90 stupnjeva).

Općenito

Dakle, što trebate zapamtiti? Simbol trokuta je zraka koja dijeli svoj vrh na pola. Na sjecištu triju zraka nalazi se središte kružnice upisano u ovaj trokut (jedini nedostatak ovog svojstva je da nema praktičnu vrijednost i služi samo za ispravno izvođenje crteža). Ona također dijeli suprotnu stranu na segmente, čiji je omjer jednak omjeru strana između kojih je ova zraka prošla. U četverokutu, svojstva su nešto složenija, ali, priznati, praktički se ne događaju u zadacima na razini škole, pa stoga program obično ne utječe na njih.

Simetrala jednakokračnog trokuta je krajnji san svakog učenika. To je ujedno i medijan (to jest, dijeli suprotnu stranu na pola) i visinu (okomitu na ovu stranu). Rješavanje problema s takvom simetralom svedeno je na Pitagorin teorem.

Poznavanje osnovnih funkcija simetrala, kao i njenih osnovnih svojstava, nužno je za rješavanje geometrijskih problema srednjeg i visokog stupnja složenosti. Zapravo, ova se zraka nalazi samo u planimetriji, tako da je nemoguće reći da će pamćenje informacija o njemu omogućiti da se nosi sa svim vrstama zadataka.