Formula Ciolkovskog: uporaba i primjer
Formula Konstantina Eduardovića Tsiolkovskog izražava maksimalnu brzinu zrakoplova, do kojeg dolazi tijekom leta. Ona se dobiva integriranjem Meshcherske jednadžbe.
Formula Tsiolkovsky
Ova formula izražava brzinu rakete koju prenose plinovi iz izgorjelog goriva. Meshcherskyjeva jednadžba i ciolkovska formula neraskidivo su povezane - Meshcherska jednadžba opisuje masu materijalne točke koja se mijenja s vremenom, dok kretanje mlaznih raketa stalno smanjuje svoju masu uslijed izgaranja goriva. Promjena brzine s promjenjivom masom (koja se u našem slučaju smanjuje) pokretnog tijela - to je ono što mlazni pogon implicira. Na njemu se temelji formula Ciolkovskog.
Kako bi se riješio niz problema teorijske mehanike u području mlaznog pogona, koristi se Meshcherska jednadžba (osnovna jednadžba materijalne točke varijabilne mase) i Tsiolkovskijeva formula (formula konačne brzine zrakoplova), koja se naziva osnovnim odnosima teorije mlaznog pogona.
Temelj za projektiranje i planiranje u području svemirskog leta upravo je formula Ciolkovskog, čiji je zaključak bio pravi proboj za istraživanje svemira.
Zadaće Tsiolkovskog
Da bi se riješio problem međuplanetarnih letova, K.E. Tsiolkovsky je raketu smatrao sredstvom za let. Izvodio je formulu koja se može upotrijebiti za određivanje ovisnosti mase zrakoplova o gorivu i brzine odvajanja produkata izgaranja rakete koja se koristi gorivom u odnosu na nju. Prikazujemo dvije njegove zadaće:
- Proučavanje kretanja tijela s promjenjivom masom s jednom reaktivnom silom koja djeluje na nju.
- Proučavanje kretanja tijela u ravnomjernom polju gravitacije promjenjive mase u blizini površine Zemlje.
predgovor
Za sve svemirske letove, početna i temeljna bila je formula Tsiolkovsky za brzinu rakete, čiji je izlaz prikazan u nastavku.
Prvo morate uzeti, grubo govoreći, za materijalnu točku. Na njega će djelovati sile gravitacije Zemlje i drugih nebeskih tijela (u trenutku polijetanja gravitacijska sila Zemlje će, naravno, biti najjača), sila otpora zraka s jedne strane i suprotno usmjerena reaktivna sila koja nastaje oslobađanjem spaljenog plina u bazi , Raketa s velikom silom izbacuje te plinove, što mu govori da je ubrzanje usmjereno nasuprot strani emisije. Sada morate te argumente predstaviti u obliku formule.
Načelo samoga raketnog leta je vrlo jednostavno. Na velikoj brzini, plin proizveden izgaranjem goriva, koji samoj raketi daje određenu silu, koja djeluje suprotno smjeru kretanja, izlazi iz rakete. Budući da se vjeruje da vanjske sile ne djeluju na raketu, sustav će biti zatvoren, a njegov zamah ne ovisi o vremenu.
Jednadžba Meshchersky
Jedan od glavnih primjera kretanja tijela s promjenjivom masom je raketa s jednim stupnjem, čija se masa mijenja samo uslijed sagorijevanja goriva u njemu. Masa takve rakete sastoji se od nepromijenjene (sama raketa i njezine nosivosti) i varijable (goriva). Takav primjer je pojednostavljeni model.
Međutim, u modernoj raketnoj proizvodnji koriste se višestupanjske rakete. Princip njihovog rada je da zbog velikog broja koraka mogu transportirati i koristiti mnogo više goriva nakon polijetanja. Nakon sagorijevanja, raketa je zabilježena kao značajan impuls (mnogo veća od one koja se može postići jednim stupnjem), a dijelovi koji su postali nepotrebni odvajaju se od baze, smanjujući ukupnu težinu za 80-90%. Međutim, da bi se izračunali parametri višestupanjske rakete, potrebno je zbrojiti pokazatelje svake njegove komponente.
Diferencijalna jednadžba Meshcherskoga opisuje gibanje materijalna točka s promjenjivom masom.
(m + dm) (υ + dυ) + dm 'υ' - mυ = Fdt - u vremenu dt (razlika između sile u vremenu t i dt + t će biti prirast).
Gdje m i υ ovise o vremenu, dt - neko vrijeme leta. Za to je formirana sila kretanja plina - dm 'υ', dm '- masa plina nastalog iz goriva. F je rezultirajuća sila.
U gore navedenom izrazu, porast mase rakete i plina i brzine juri na nulu, tako da izraz ima sljedeći oblik:
mdυ = υ''dm + Fdt,
štoviše, υ "je jednaka razlici između brzine i brzine plina i brzine protoka plina.
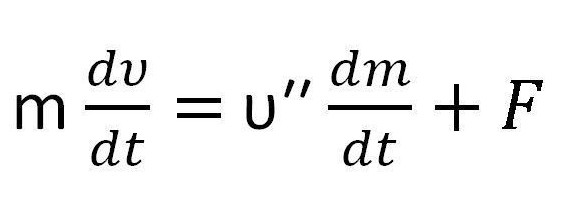 - jednadžba u formi počinje se podudarati s Newtonovim drugim zakonom - F = ma = m
- jednadžba u formi počinje se podudarati s Newtonovim drugim zakonom - F = ma = m
To se zove Meshchersky jednadžba.
Izvođenje formule Tsiolkovsky
Potrebno je izvesti formulu koja opisuje gibanje tijela s promjenjivom masom. Formula Tsiolkovsky je takva. Rezultat je prikazan u nastavku.
U tim izračunima pretpostavlja se da vanjske sile ne djeluju na pokretno tijelo, to jest, F = 0.
Zatim mdυ = υ''dm
Budući da je utjecaj vanjskih sila na leteću raketu nula, ona se kreće u ravnoj liniji, a brzina kretanja je suprotna brzini plina. Prema tome, υ = -υ ''
Ispada da je izraz koji treba integrirati.
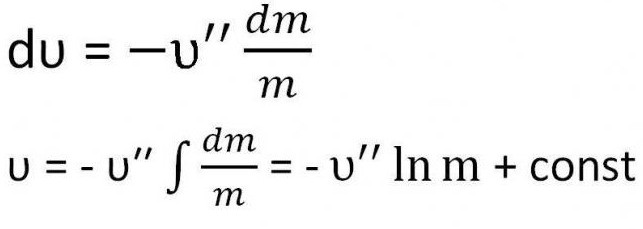
Potrebno je pronaći konstantu. Da biste to učinili, dovoljno je zamijeniti početne uvjete jednadžbi - brzina je nula, a masa je zbroj mase goriva i mase rakete (m 0 + m)
Općenito govoreći, m u formuli sastoji se od dva parametra - od nosivosti i dizajna rakete. Nosivost je ukupna težina tereta i posade.
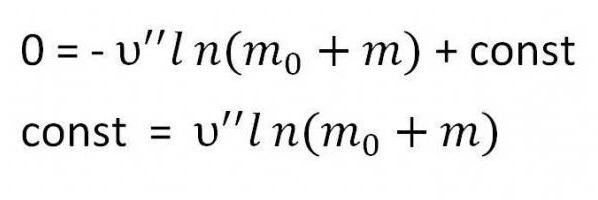
Zamjenjujemo pronađenu konstantu u formuli. Kao rezultat, dobiva se izraz tražene formule.
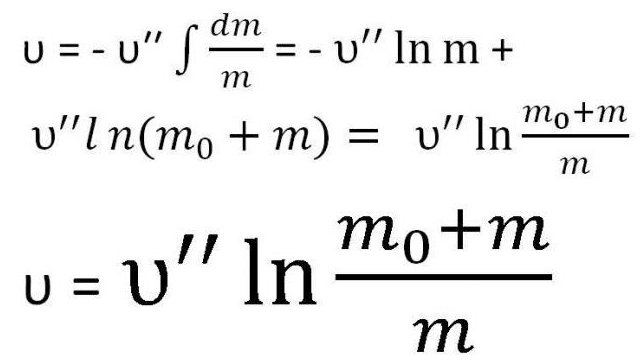
To je jedna od varijacija Ciolkovske formule za brzinu. Međutim, ponekad je potrebno uzeti u obzir upravo masu. Stoga se ponekad piše na sljedeći način:
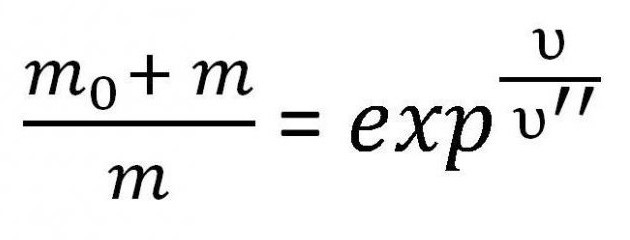
Ova formula se koristi za izračunavanje mase goriva koja je potrebna za razvoj određene brzine u određenim uvjetima.
Nadalje ću razmotriti mali zadatak. Pretpostavimo da raketa treba razviti prvu kozmičku brzinu za rotaciju duž Zemljine orbite. Tada prvo trebate izračunati masu naravno, gorivo. Onda je vrlo jednostavno izraziti ga iz formule Tsiolkovsky.
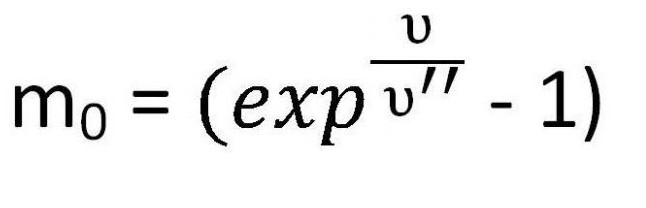
Relativistička mehanika
Sve gore navedene formule mogu se koristiti samo u slučaju kada je brzina rakete mnogo manja od brzine svjetlosti (υ < Međutim, ako se brzina rakete može usporediti sa brzinom svjetlosti, tada je potrebno primijeniti druge zakone. Neka su m i υ masa rakete u stanju i brzina u bilo kojem trenutku t, a υ 'i m' brzina otpuštanja plina i njezina masa u isto vrijeme. To jest, m 'je masa otpuštenog plina, pa je njegova vrijednost za izračun nevažna, m' = 0. Potrebno je napisati zakon očuvanja momenta i zakon očuvanja energije u relativističkoj mehanici, zatim razlikovati prvu jednadžbu, s obzirom da je m '= 0 i dobiti izraz treći. gdje je u brzina emisije plinova. Temeljem zakona dodavanja brzina u relativističkoj mehanici, ovaj izraz slijedi. Potrebno ga je pretvoriti s obzirom na υ 'i integrirati kako bi se dobila konačna verzija jednadžbe. I tada dobivamo formulu Tsiolkovsky za brzinu, usporedivu sa brzinom svjetlosti. To se također može nazvati relativističkom formulom Tsiolkovsky. Možete pomalo zakomplicirati zadatak i uzeti kao primjer raketu s nekoliko stupnjeva. Dakle, formula Tsiolkovsky za višestupanjsku raketu je zbroj parametara potrebnih za izračun. To jest, da biste izračunali brzinu za višestupanjsku raketu, trebali biste zbrojiti brzinu svakog od sastavnih dijelova. Osnova svih svemirskih letova je formula Tsiolkovsky. Prilikom izračunavanja leta važno je jasno razumjeti koji postotak energije dobivene nakon izgaranja goriva koristi se kao koristan rad? Dakle, učinkovitost se naziva omjer kinetičke energije rakete i plinove nakon izbacivanja. Označite m i m 'za masu rakete na početku i na kraju leta, kontinuirano vrijeme t. Prema tome, - brzina izbacivanja plinova. Tada, prema formuli Tsiolkovskog, učinkovitost raketnog motora može se naći na sljedeći način: Treba napomenuti da je ova učinkovitost vrlo mala i ne prelazi 5%, štoviše, kao u toplinskim motorima, ovaj pokazatelj je jednak 80%. Neki resursi koriste malo drukčiju formulu Tsiolkovskog, jednadžbu u kojoj se umjesto parametra υ koristi drugi parametar. , Prvo pitanje koje nam pada na pamet je pitanje dimenzionalnosti. Za razliku od brzine, zamah ima drugačiju dimenziju, što će proturječiti suštini formule. Međutim, specifični impuls sam po sebi podudara u dimenziji s brzinom. Specifični impuls označava broj sekundi kada će motor, potrošivši jedinicu goriva, primiti jedinicu sile. Koristi se isključivo u opisu mlaznog motora. Formula Ciolkovskog za višestupanjsku raketu također se koristi u dizajnu rakete. Za to se koristi potpuno logičan odnos, koji je praktički izravno proporcionalan - što se više goriva koristi pri letenju, veća je i masa same rakete. To je zbog činjenice da su za transport velikih količina goriva, odnosno, potrebni veliki spremnici, pa se zbog toga povećava veličina broda, pa čak i sam motor. Jedno rješenje problema je uporaba krutih goriva, koja zahtijeva manje uvjeta skladištenja. Međutim, u ovom trenutku ona ima najmanji specifični impuls postojećih. Formula Ciolkovskog također se koristi za izračunavanje potrebne količine goriva za razvoj određene brzine - obično jedna od četiri kozmičke. 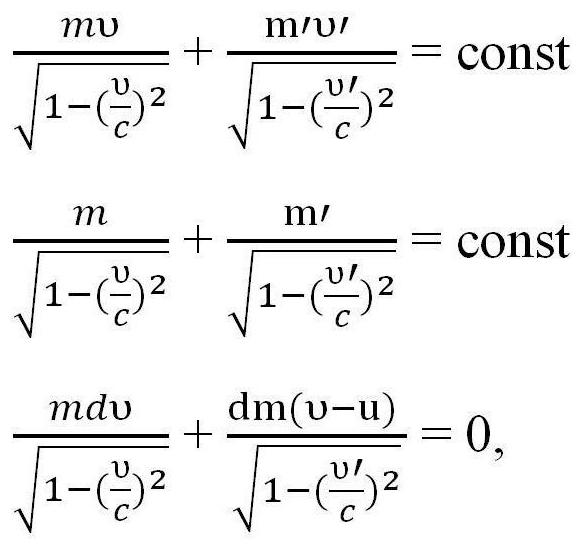
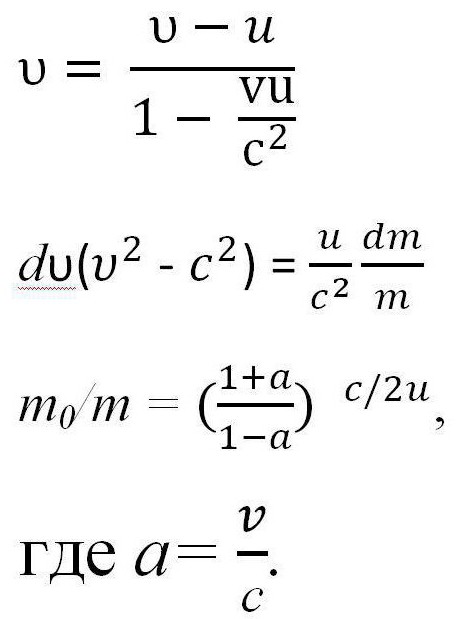
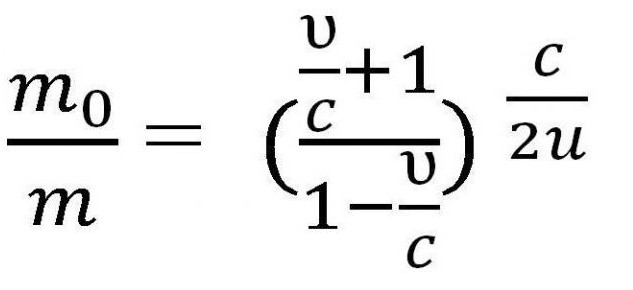
Nekoliko zaključaka iz formule Tsiolkovsky
Raketna učinkovitost
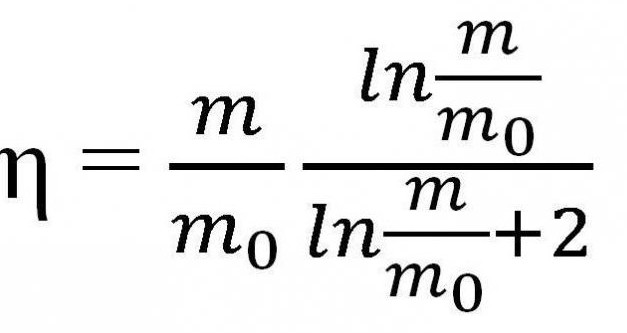
Drugi oblik formule
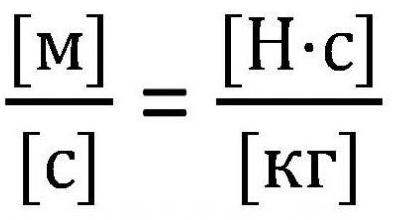
Koristite za izradu projektila
Svemirske brzine