Što je stožac? Koncept i fotografija

Stereometrija je važan dio geometrije, čiji su predmet istraživanja svojstva i karakteristike figura u trodimenzionalnom prostoru. U ovom članku razmotrit ćemo jednu od takvih volumetrijskih brojki. Upoznajmo se s pitanjem što je konus.

Konusna figura

Dajemo najopćenitiju definiciju konusa. Pod tom slikom razumijemo površinu, koja se formira kao rezultat spajanja ravnih segmenata određene točke u prostoru sa svim točkama dane krivulje. U tom slučaju, navedena točka u prostoru ne bi trebala biti u ravnini krivulje. Primjerice, ako krivulja ima oblik parabole, tada će se broj dobiven opisanom metodom nazvati parabolični konus, ako je krivulja elipsa, konus će biti eliptičan i tako dalje.

Nakon što damo geometrijsku definiciju onoga što je konus, predstavljamo fotografiju koja prikazuje vizualno moguće oblike ove figure.

Gledajući ovu fotografiju, mnogi su u njoj vidjeli oblik dječjeg šešira, koji je nosio Buratino, šalicu za vafl od sladoleda u obliku roga ili upozorenje narančasti i crni cestovni konus.

Stožac geometrijskih elemenata

Da bismo bolje razumjeli pitanje što je konus, valja navesti geometrijska imena elemenata te prostorne figure.

Stožac je omeđen s dvije površine. Prvi se zove baza. To je ravnina koja je ograničena gore navedenom krivuljom. Na primjer, može biti krug ili elipsa. Druga površina je strana oblika i naziva se konična. Ne leži u istoj ravnini, već se može pretvoriti u ravnu sliku, kao što će biti objašnjeno u nastavku.

Jedan od važnih elemenata stošca je njegov vrh. Ova točka ograničava stožastu površinu. Na njega su povezane sve točke osnovne krivulje.

Segment koji povezuje vrh baze, naziva se generica, ili tvori konus. S druge strane, krivulja koja graniči s bazom nazvana je direktnom linijom, ili vodičem.

Područja stožaste površine i podloge čine ukupnu površinu konusa. Volumen prostora kojim ta dva područja ograničavaju je volumen konusa.

Okrugli ravni konus i njegove linearne karakteristike

Iznad je dana opća definicija što je konus. Ipak, često u praksi iu geometrijskim problemima postoji specifičan oblik ove figure - ravan kružni konus. To je prikazano u nastavku.

Osnova ove brojke je krug. To se naziva ravno jer okomica koja je pala na svoju bazu s visine presjeći će krug u njegovom točnom središtu. Ako taj uvjet nije zadovoljen, onda možemo govoriti o nagnutom konusu.

Linija koja spaja vrh s središtem kruga naziva se osom slike. To je također i os rotacije konusa. Doista, ako uzmete pravokutni trokut i počnete ga rotirati oko jedne od nogu, tada će rezultirajuća figura biti ravni konus s okruglom bazom. Ovaj postupak dobivanja konusa prikazan je shematski dolje.

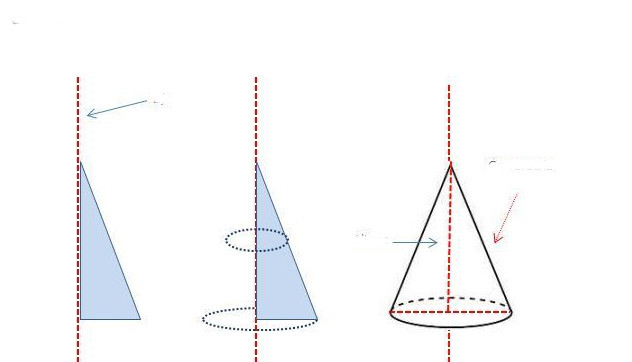
Može se vidjeti da će generator biti jednak duljini hipotenuze trokuta. Noga, oko koje je izvedena rotacija, postat će visina trodimenzionalne figure, a druga će biti jednaka radijusu konusa (radijus kružne baze).

Jedna od važnih značajki dotične figure je da su duljine svih generatora za nju jednake jedna drugoj. Ta nam činjenica, koristeći Pitagorin teorem, piše matematičku vezu između tri glavna linearna parametra oblika:

g ² = r ² + h ²

Kvadrat generatora pravog kružnog konusa je jednak zbroju kvadrata njegovog radijusa r i visine h.

Ispitujući pitanje što je konus ravna crta s kružnom bazom, pokažimo kako je moguće njezina površina i volumen.

Određivanje površine

Kao što je već spomenuto, površina figure je oblikovana koničnom površinom i ravnim dnom. Koje je njihovo područje? S povjerenjem možete odgovoriti na to pitanje ako pogledate ravan sken kružnog konusa. Rezanjem podloge sa bočne površine, i rezanjem potonje uzduž generatora, dobivamo sljedeći rezultat.

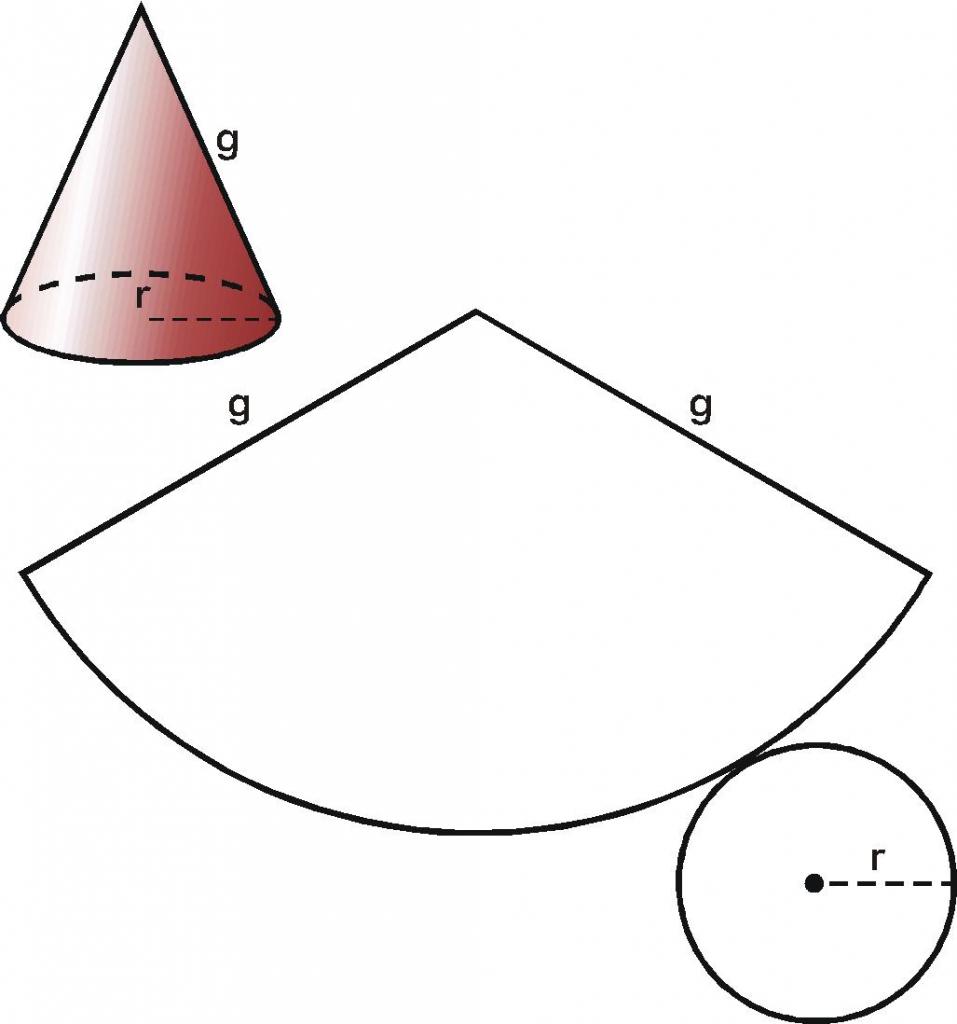
Nema problema s određivanjem površine kruga. Formula za njezino područje poznata je svakom studentu. Zapišite:

S _o = pi * r ²

Simbol S _o je područje baze slike.

Bočna površina stošca na ravnom skeniranju predstavljena je kružnim sektorom čiji je radijus jednak duljini generatora, a duljina luka na kojem počiva sektor jednaka je duljini opsega baze. Ovi podaci nam omogućuju da jedinstveno odredimo područje sektora. Nećemo davati interne izračune za dobivanje formule za kvadrat S _b bočne površine konusa. Pišemo konačni rezultat:

Sb = pi * g * r

Budući da je generica g uvijek veća od radijusa r, površina bočne površine slike će, za bilo koje parametre, premašiti područje baze.

Formula za ukupnu površinu poprima oblik:

S = S _o + S _b = pi * r * (r + g)

Određivanje volumena slike

Čitatelji su možda primijetili da oblik konusa podsjeća na neku piramidu, samo je njena bočna površina glatka i ne rebrasta, poput piramide. Ova analogija ima geometrijsko opravdanje, budući da se povećanje broja bočnih strana piramide u beskonačnost prevodi u stožac. Ta činjenica omogućuje da se za volumen stošca zapiše točno jednaka formula kao za volumen piramide. Imamo:

V = 1/3 * h * S _o

Napominjemo da nije bitno koja je zatvorena krivulja osnova osnove konusa, također nije bitno je li lik ravan ili kos, formula će vrijediti u svim tim slučajevima.

Za konus kruga, izraz za V poprima određeni oblik:

V = 1/3 * pi * r ^{2 *} h

Zadatak određivanja površine konusa kroz njegov volumen

Pokazujemo kako koristiti pisane formule.

Pretpostavimo da je volumen okruglog konusa 50 cm3. Potrebno je izračunati njegovu površinu ako je radijus r tri puta manji od visine h.

Pišemo formulu za volumen i odnos visine h s radijusom r u skladu sa stanjem problema:

V = 1/3 * pi * r ^{2 *} h;

h = 3 * r.

Iz tih jednadžbi dobivamo:

V = 1/3 * pi * r ² * 3 * r =>

r = (V / pi) ≈ 2.516 cm;

h = 3 * ∛ (V / pi) ≈ 7.547 cm.

Dobivene vrijednosti omogućuju izračunavanje duljine glavnog generatora konusa:

g = √ (h2 + r2) = 7,955 cm.

Formula za površinu slike je:

S = pi * r * (r + g)

Utvrdili smo sve potrebne količine (r i g). Zamjenjujući njihove numeričke vrijednosti u jednakost, dobivamo odgovor: S = 82,72 cm2.