Što je snaga abecede

U računalnoj znanosti abeceda je znakski sustav, kojim možete poslati informativnu poruku. Da bismo razumjeli bit te definicije, evo nekoliko dodatnih teorijskih činjenica:

1. Sve poruke sastoje se od abecede. Na primjer, ovaj članak je poruka. Tada se sastoji od znakova ruske abecede.
2. Pod simbolom možemo razumjeti minimalnu značajnu česticu abecede. I nedjeljive čestice nazivaju se atomi. Znakovi ruske abecede su "a", zatim "b", "c" i tako dalje.
3. U teoriji, abeceda ne mora biti kodirana na bilo koji način. Na primjer, u tiskanoj knjizi simboli abecede znače sami sebe, što znači da nemaju nikakvo kodiranje.

Ali u praksi imamo sljedeće: računalo ne razumije što su slova. Stoga, da bi se poslala informativna poruka, ona se prvo mora kodirati na jeziku razumljivom računalu. Da bismo nastavili dalje, potrebno je uvesti dodatne uvjete.

Što je snaga abecede

Pod abecednom moći podrazumijevamo ukupan broj znakova u njemu. Da biste saznali koja je snaga abecede, trebate samo brojati broj znakova u njoj. Hajde da shvatimo. Za rusku abecedu, snaga abecede je 33 ili 32 znaka, ako ne koristite "e".

Pretpostavimo da se svi znakovi naše abecede susreću s jednakom vjerojatnošću. Ova se pretpostavka može shvatiti na sljedeći način: pretpostavimo da imamo torbu s potpisanim kockama. Broj kocki u njemu je beskonačan, a svaki je potpisan sa samo jednim simbolom. Zatim, s ravnomjernom raspodjelom, bez obzira koliko kockica izašli iz vrećice, broj kocki s različitim simbolima će biti isti, ili će se skloniti tome s povećanjem broja kocki koje izvučemo iz vrećice.

Procjena težine informativnih poruka

Prije gotovo stotinu godina, američki inženjer Ralph Hartley izveo je formulu s kojom možete procijeniti količina informacija u poruci. Njegova formula radi za jednako vjerojatne događaje i izgleda ovako:

i = log ₂ M

Gdje je "i" broj nedjeljivih informacijskih atoma (bitova) u poruci, "M" je snaga abecede. Slijedimo. Pomoću matematičkih transformacija možemo odrediti da se snaga abecede može izračunati na sljedeći način:

M = 2 ⁱ

Ova formula u općem obliku postavlja vezu između broja jednako vjerojatnih događaja "M" i količine informacija "i".

Izračunajte snagu

Najvjerojatnije već znate iz tečaja računalstva u školi da se u modernim računalnim sustavima koji se temelje na von Neumannovoj arhitekturi koristi binarni sustav kodiranja informacija. Ovako su kodirani i programi i podaci.

Kako bi se prikazao tekst u računalnom sustavu, koristite jedinstveni kod od osam bitova. Kôd se smatra uniformnim jer sadrži fiksni skup elemenata - 0 i 1. Vrijednosti u takvom kodu su određene specifičnim redoslijedom tih elemenata. Pomoću osmobitnog koda možemo kodirati poruke težine 256 bita, jer Hartleyjeva formula: M8 = 2 ⁸ = 256 bita informacija.

Ova situacija s kodiranjem znakova u binarnom kodu razvila se povijesno. Ali teoretski bismo mogli koristiti druge alfabete za prikaz podataka. Tako, na primjer, u abecedi od četiri slova, svaki znak bi imao težinu od ne jednog, nego dva bita, u abecedi od osam znakova - 3 bita, i tako dalje. To se izračunava pomoću binarnog logaritma danog gore ( i = log ₂ M ).

Budući da je u abecedi s kapacitetom od 256 bita, dodijeljeno osam binarnih znamenki za jedan znak, odlučeno je uvesti dodatnu mjeru informacija - bajtova. Jedan bajt sadrži jedan znak tablice ASCII koda i sadrži osam bitova.

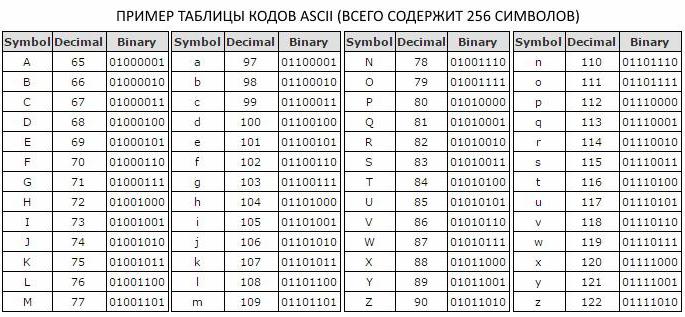
Kako mjeriti informacije

в прописном и строчном варианте, цифры, символы знаков препинания и другие базовые символы. Osam-bitno kodiranje tekstualnih poruka, koje se koristi u ASCII kodnoj tablici, omogućuje vam da uklopite osnovni skup latiničnih i ćiriličnih znakova u velika i mala slova, brojeve, interpunkcijske znakove i druge osnovne znakove.

Kako bi izmjerili veće količine podataka, koristite posebne prefikse za riječi byte i bit. Takvi prilozi prikazani su u donjoj tablici:

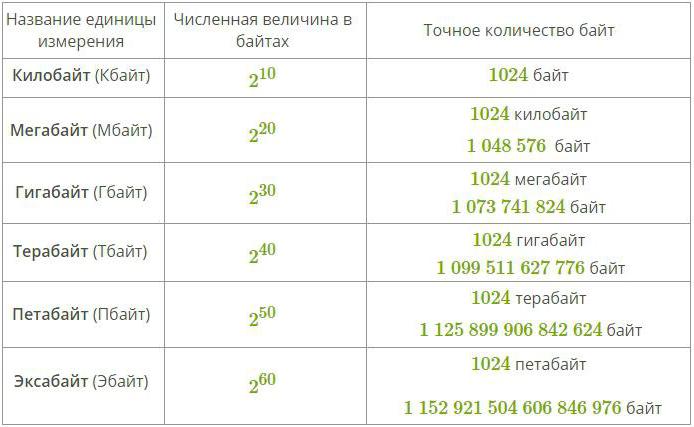
Mnogi ljudi koji su proučavali fiziku tvrde da bi bilo racionalno koristiti klasične prefikse za označavanje jedinica informacija (kao što su kilo i mega), ali zapravo to nije posve točno, jer takvi prefiksi za vrijednosti označavaju množenje jednog ili drugog stupnja od deset. kada se binarni sustav mjerenja koristi svugdje u računalnoj znanosti.

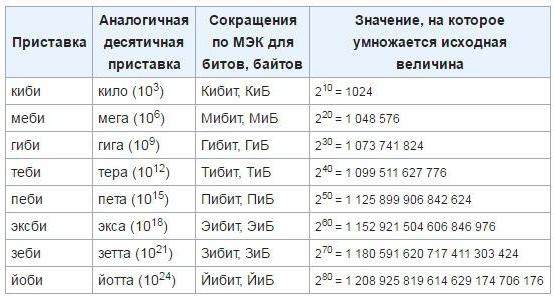
Ispravite nazive jedinica podataka

Kako bi se uklonile netočnosti i nepogodnosti, Međunarodna komisija za elektrotehniku ​​odobrila je u ožujku 1999. nove jedinice jedinicama koje se koriste za određivanje količine informacija u tehnologiji elektroničkog računalstva. Takvi prefiksi su "mebi", "kibi", "gibi", "tebi", "eksbi", "petit". Do sada se ove jedinice još nisu ukorijenile, tako da je najvjerojatnije potrebno vrijeme za uvođenje ovog standarda i početak široke uporabe. Kako napraviti prijelaz s klasičnih jedinica na novo odobrene, možete odrediti sljedeću tablicu:

Pretpostavimo da imamo tekst koji sadrži K znakova. Zatim, koristeći abecedni pristup, možete izračunati količinu informacija V, koju sadrži. Bit će jednak proizvodu snage abecede prema težini informacija jednog znaka u njoj.

Hartleyevom formulom znamo izračunati količinu informacija kroz binarni logaritam. Uz pretpostavku da je broj znakova abecede jednak N i da je broj znakova u zapisu informativne poruke jednak K, dobivamo sljedeću formulu za izračunavanje volumena informacija poruke:

V = K ₂ log ₂ N

Abecedni pristup ukazuje da će volumen informacija ovisiti samo o snazi ​​abecede i veličini poruka (to jest, broju znakova u njoj), ali ni na koji način neće biti povezan sa semantičkim sadržajem za osobu.

Primjeri izračuna snage

U učionici informatika često daje zadatak pronalaženja moći abecede, dužine poruke ili volumena informacija. Evo jednog od sljedećih zadataka:

"Tekstualna datoteka zauzima 11 KB prostora na disku i sadrži 11264 znakova. Odredite snagu abecede ove tekstualne datoteke."

Što će biti rješenje, možete vidjeti na slici ispod.

Dakle, abeceda s kapacitetom od 256 znakova nosi samo 8 bitova informacija, što se u računalnoj znanosti naziva jednim bajtom. Bajt opisuje 1 znak ASCII tablice, koja, ako razmislite o tome, uopće nije puno.

Je li jedan bajt mnogo ili malo?

Moderna skladišta podataka poput podatkovnih centara Googlea i Facebooka sadrže ne manje od desetaka petabajta informacija. Točna količina podataka, međutim, bit će teško izračunati čak i sama, jer tada ćete morati zaustaviti sve procese na poslužiteljima i zatvoriti korisnike pristup snimanju i uređivanju njihovih osobnih podataka.

No, kako bi se zamislili takve nepojmljive količine podataka, potrebno je jasno shvatiti da se sve sastoji od malih detalja. Potrebno je razumjeti koja je snaga abecede (256) i koliko bitova sadrži 1 bajt informacija (kao što se sjećate, 8).