Apsolutno elastičan udarac. Apsolutno neelastični udar

Zakoni očuvanja momenta su temeljni zakoni prirode. Primjer primjene ovih zakona je fenomen sudara. Apsolutno elastični i neelastični udarci - promjena stanja tijela kao rezultat kratkotrajne interakcije tijekom njihovog sudara.

Mehanizam interakcije

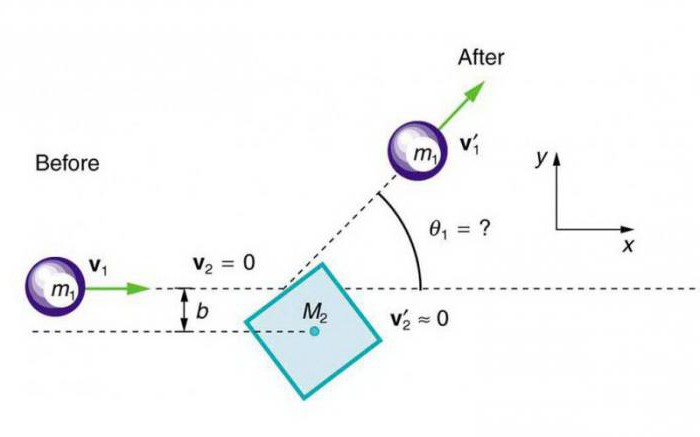
Najjednostavniji tip interakcije fizičkih tijela je središnji sudar kuglica koje imaju idealan geometrijski oblik. Vrijeme kontakta ovih objekata je u stotinkama sekunde.

U skladu s definicijom razmatra se središnji štrajk u kojem linija sudara prelazi središta kuglica. U ovom slučaju, putanja interakcije je ravna crta koja se u trenutku dodira točno s elementom kontaktne površine. U mehanici se razlikuju apsolutno elastični i neelastični udarci.

Vrste interakcija

Apsolutno neelastični utjecaj uočen je u sudaru dvaju tijela plastičnih materijala ili plastičnih i elastičnih tijela. Nakon što se završi, brzina sudarajućih objekata postaje ista.

Apsolutno elastičan utjecaj uočava se u interakciji predmeta od elastičnih materijala (na primjer, dvije kuglice od tvrdog čelika ili kuglice nekih vrste plastike i tako dalje).

faze

Proces elastičnog sudara odvija se u dvije faze:

• Faza I - trenutak nakon početka sudara. Sile koje djeluju na kuglice povećavaju se s povećanjem naprezanja. Povećanje naprezanja popraćeno je promjenom brzine objekata. Tijela čija je brzina bila veća, usporavaju kretanje, a tijela ubrzavaju nižom brzinom. Kada deformacija postane maksimalna, brzina kuglica nakon apsolutno elastičnog udara postaje ravnoteža.
• Faza II. Od trenutka koji karakterizira početak drugog stupnja elastičnog udara, vrijednost deformacija se smanjuje. U tom slučaju, deformacijske sile guraju kuglice. Nakon što deformacija nestane, kuglice se uklanjaju i potpuno vraćaju u prvobitni oblik i kreću se različitim brzinama. Tako, na kraju drugog stupnja, središnji apsolutno elastični utjecaj transformira cijeli zalihe potencijalne energije elastično deformiranih tijela u kinetičku energiju.

Izolirani sustavi

U praksi nijedan udarac nije apsolutan (elastičan ili neelastičan). Sustav u svakom slučaju komunicira s okolnom tvari, razmjenjuje energiju i informacije s okolinom. No, za teorijska proučavanja dopušteno je postojanje izoliranih sustava u kojima se interagira isključivo predmeti istraživanja. Na primjer, moguće su i apsolutno neelastični i apsolutno elastični udar lopte.

Vanjske sile na takav sustav ne djeluju ili se njihov utjecaj kompenzira. U izoliranom sustavu zakon konzervacije impulsa djeluje u potpunosti - sačuvan je ukupni impuls između sudarajućih tijela:

M = m _i v _i = const.

Ovdje "m" i "v" je masa određene čestice ("i") izoliranog sustava i njegov vektor brzine, respektivno.

Da bismo uštedjeli mehaničku energiju (poseban slučaj općeg zakona energija), postoji potreba da sile koje djeluju u sustavu budu konzervativne (potencijalne).

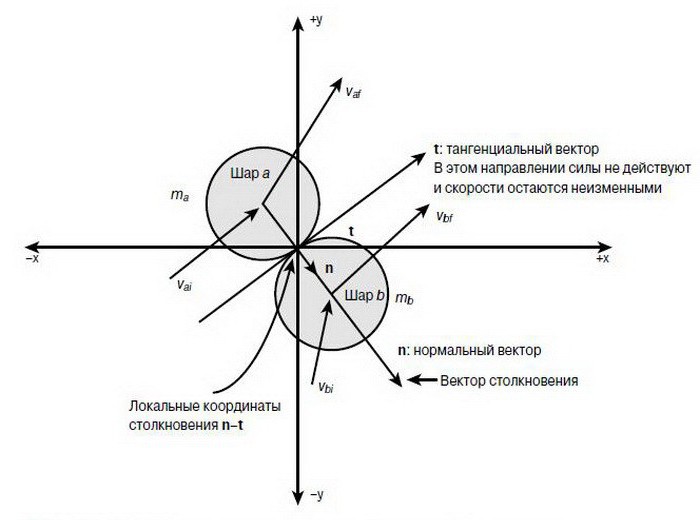
Konzervativne snage

Konzervativne sile su one koje mehaničku energiju ne pretvaraju u druge vrste energije. Te sile su uvijek potencijalne - to jest, posao koji takve sile izvode duž zatvorene petlje je nula. U suprotnom, sile se nazivaju disipativnim ili nekonzervativnim.

U konzervativnim izoliranim sustavima mehanička energija između tijela sudara također su spremljene:

W = Wk + Wp = m (mv 2/2) + Wp = const.

Ovdje su Wk i Wp kinetičke (k) i potencijalne (p) energije.

Da biste provjerili relevantnost zakoni o uštedi energije (od navedenih formula), ako se apsolutno elastična tijela udare pod uvjetom da se jedna od kuglica ne pomakne prije sudara (brzina nepokretnog tijela je v ₂ = 0), znanstvenici su izvukli sljedeću pravilnost:

m ₁ v ₁ Ki = m ₁ U ₁ + m ₂ U ₂

(m ₁ v ₁ ² ) / 2 × Ke = (m ₁ U ₁ ² ) / 2 + (m ₂ U ₂ ² ) / 2.

Ovdje m ₁ i m ₂ je masa prve (udarne) i druge (fiksne) kugle. Ki i Ke su koeficijenti koji pokazuju koliko puta je zamah dvaju kuglica (Ki) i energije (Ke) porastao u trenutku kada je napravljen apsolutno elastičan udarac. v ₁ - brzina valjanja kugle.

Budući da bi ukupni impuls sustava trebao biti očuvan pod bilo kojim uvjetima sudara, treba očekivati ​​da će koeficijent oporavka impulsa biti jednak jedinici.

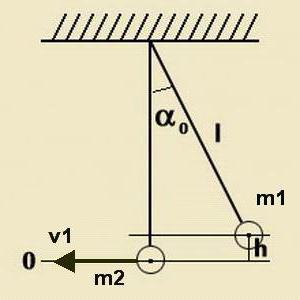
Izračun sile udarca

Brzina udarca (skrenuta na nit) lopte koja leti na fiksnoj (slobodno suspendiranoj) kugli određena je formulom za zakon očuvanja energije:

m ₁ gh = (m ₁ v ₁ ² ) / 2

h = l-lcosa = 2lsin2 (a / 2).

Ovdje h je odstupanje ravnine udarne lopte u odnosu na ravninu fiksne kugle. l je duljina vlakana (apsolutno identična) na kojima su kuglice suspendirane. α je kut otklona udarne kugle.

Sukladno tome, apsolutno elastičan udar u sudaru udarca (skrenut na navoj) i fiksne (slobodno visi na niti) izračunava se po formuli:

v ₁ = 2sin (a / 2) lgl.

Istraživački objekt

U praksi se jednostavna instalacija koristi za izračunavanje interakcijskih sila. Namijenjen je proučavanju tipova udara dvije kuglice. Instalacija je tronožac na tri vijka koji vam omogućuju da ga postavite horizontalno. Na tronožac je središnji stalak, na gornji kraj kojeg je pričvršćen poseban ovjes za kuglice. Elektromagnet je pričvršćen na štap, koji privlači i drži, na početku eksperimenta, jednu od kuglica (šok-loptu) u otklonjenom stanju.

Veličina početnog kuta otklona ove kugle (koeficijent α) može se odrediti iz lučno zakrivljene skale divergirajuće u oba smjera. Magnituda njezine zakrivljenosti odgovara putanji kretanja međudjelujućih kugli.

Proces istraživanja

Prvo se priprema par kuglica: ovisno o zadacima, uzimaju se elastične, neelastične ili dvije različite loptice. Masa loptica se bilježi u posebnoj tablici.

Zatim je udarni element usidren na elektromagnet. Na skali odredite kut otklona navoja. Zatim je elektromagnet isključen, gubi svojstva privlačenja, a lopta se spušta prema dolje u luku, sudarajući s drugom, slobodnom, nepomično visećom loptom, koja zbog impulsa (udarca) odstupa od određenog kuta. Veličina odstupanja je fiksna na drugoj skali.

Apsolutno elastični utjecaj izračunat na temelju eksperimentalnih podataka. Da bi se potvrdila istinitost zakona očuvanja momenta i energije u slučaju elastičnih i neelastičnih sudara dvaju kugli, njihove se brzine određuju prije i nakon sudara. Temelji se na balističkoj metodi mjerenja brzine kretanja kuglica prema veličini njihovog otklona. Ta se vrijednost mjeri na ljestvici napravljenoj u obliku kružnih lukova.

Značajke izračuna

Pri izračunavanju utjecaja u klasičnoj mehanici ne uzimaju se u obzir brojni pokazatelji:

• vrijeme sudara;
• stupanj deformacije međusobno povezanih objekata;
• heterogenost materijala;
• brzina deformacije (prijenos impulsa, energija) unutar lopte.

Sukob bilijarskih kugli dobar je primjer elastičnog udarca.