Algebarska progresija: formule i primjeri rješenja
U ovom će članku raspravljati o algebarskoj progresiji, formulama potrebnim za rješavanje problema s njezinim sudjelovanjem, kao i neke primjere njihove uporabe. Radi cjelovitosti, ukratko ćemo govoriti o drugoj vrsti progresije - geometrijskoj.
Pojam algebarske progresije

Svaka serija brojeva koja je uređena prema nekom zakonu može se nazvati progresijom. Za rješavanje praktičnih problema najpopularnije i najkorisnije su dvije vrste takvih serija: algebarska i geometrijska. Razmotrite prvi od njih detaljnije.
Algebarski se često naziva aritmetička progresija. Matematički, to znači sljedeće:
a n = a n-1 + d
To jest, govorimo o takvom numeričkom nizu u kojem se bilo koji od njegovih članova razlikuje od prethodnog ili slijedećeg istim brojem d. Taj se broj naziva razlikom (može se odrediti pronalaženjem razlike između dva susjedna elementa progresije).
Prema toj definiciji, napredak koji razmatramo ima početak, ali nema kraja. Uvijek počinje s pojmom a 1 (bilo koji stvarni broj), a zatim nastavlja sa zbrajanjem tog člana s razlikom d. Prema tome, može biti beskonačno povećana (d> 0) ili opada (d <0). Situacija kada je d = 0 također se može smatrati posebnim slučajem aritmetičke progresije koju predstavlja beskonačni slijed jednakih brojeva.
Formula za pronalaženje proizvoljnog člana
Kao što je gore objašnjeno, razmatrani tip progresije je jedinstveno određen njegovim prvim elementom i razlikom, međutim to se pravilo primjenjuje na sve druge vrijednosti. Na primjer, poznavanje dvaju proizvoljnih elemenata ili jednog elementa i zbroja određenog broja članova također jedinstveno određuje progresiju.
Za izračun n-tog elementa možete uspješno koristiti sljedeću formulu:
a n = a 1 + (n - 1) * d
Očiglednost valjanosti ovog izraza je nesumnjiva i svatko ga može potvrditi zamjenom malih vrijednosti n.
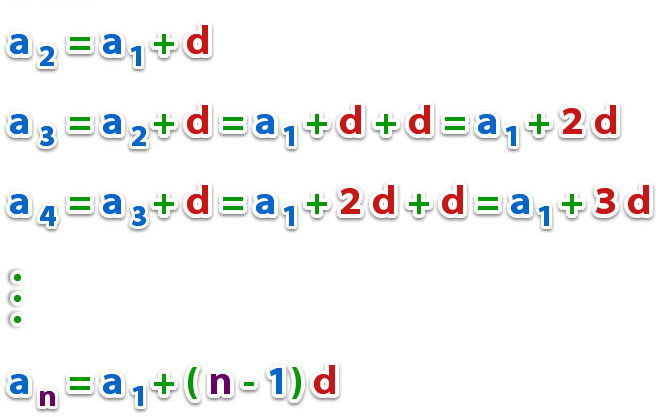
Formula za vraćanje napredovanja dva poznata elementa
U školskom toku algebre takvi su problemi tipični za progresiju: postoje dva elementa a n i m , a n> m, potrebno je na njima izgraditi cijeli napredak.
Taj se problem rješava pomoću formule za n-tog člana. Pišemo dva odgovarajuća izraza:
a n = a 1 + (n - 1) * d;
a m = a 1 + (m - 1) * d
Pronađite razliku između prvog i drugog (znak jednakosti je sačuvan):
a n - m = (n - m) * d =>
d = (a n - a m ) / (n - m)
Vidimo kako je lako pronaći razliku progresije, ako su poznata dva njena člana: da bi to učinili, oduzmite manji od većeg u redu, a zatim razdvojite dobivenu razliku za razliku od njihovih rednih brojeva.
Nakon što se pronađe razlika, lako je izračunati prvi pojam (da biste to učinili, koristite bilo koji od prva dva izraza).
Zbroj algebarske progresije
Drugi niz tipičnih zadataka za napredovanje je pronalaženje sume njihovih članova. Slijedi odgovarajuća formula algebarske sume progresije:
S n = ∑ i = 1 n (a i ) = n * (a 1 + a n ) / 2
Odnosno, za određivanje zbroja prvih pojmova od n, treba izračunati zbroj samo dva od njih (prvi i n), pomnožiti ga s brojem članova n i podijeliti rezultat na pola.
Izostavili smo matematički dokaz tog izraza, ali još uvijek pružamo logičan dokaz. Može se primijetiti da, s obzirom na svojstvo razmatranog tipa progresije, sljedeća jednakost uvijek ima:
a 1 + a n = a 2 + a n-1
Doista, drugi je pojam veći od prvog pojma s d, ali istim pretposljednjim ( n-1 ) je manji od posljednjeg ( n ). U slučaju para elemenata, dobivamo točno polovicu takvih iznosa iz ukupnog broja elemenata (n / 2), odakle slijedi reducirana formula za S n .

Smatra se da je istaknutu značajku aritmetičke progresije prvi put utvrdio Karl Gauss, poznati matematičar s kraja 18. - prve polovice 19. stoljeća, kada je u svom umu nekoliko sekundi izračunao zbroj prirodnih brojeva od jedan do 100.
Primjeri rješavanja problema
Razmotrite dva primjera algebarske progresije.
1. Poznato je da je 9. pojam 7, a 21. je 51. Potrebno je pronaći prvih 5 članova ove aritmetičke progresije.
Uvjet problema omogućuje nam da odmah izračunamo razliku d, primjenjujući formulu s n i a m , što je zapisano gore. Imamo:
d = (a n - a m ) / (n - m) = (51 - 7) / (21 - 9) = 3,667
Po primitku razlike d izvršili smo zaokruživanje na 3 decimalna mjesta.
Sada možete izračunati prvi element serije. Da biste to učinili, upotrijebite podatke za 9 članova:
a 9 = a 1 + d * 8 => a 1 = a 9 - d * 8 = 7 - 3,667 * 8 = -22,336
Kako bi riješili problem, ostaje da poduzmete posljednji korak: dodajte sukcesivno 4 puta vrijednost d na prvi element. Dobivamo:
a 1 = -22.336;
a2 = -22,336 + 3,667 = -18,669;
a3 = -18.669 + 3.677 = -15.002;
a4 = -15,002 + 3,667 = -11,335;
a 5 = -11,335 + 3,667 = -7,668
Sjetite se da su sve izračunate vrijednosti važeće do trećeg decimalnog mjesta.
2. Radnici su presavinuli pilane u obliku piramide. Poznato je da su položili samo 33 trupca, a do kraja piramide nedostajala su samo tri trupca. Potrebno je odrediti koliko je redova trupaca položeno radnika.
Odgovor na ovo pitanje je riješiti algebarsku progresiju, ali kako bismo nastavili s tim, trebamo pažljivo riješiti ovo stanje.
Prvo, budući da se trupci zbrajaju s piramidom, to znači da je u svakom prethodnom redu bio još jedan log, d. 1. Drugo, ako je poznato da su samo tri trupca nedostajale prije dovršetka piramide, tada su ostala dva gornja reda. prazna:
a 1 = 1, a 2 = a 1 + d = 2, a 1 + a 2 = 3
Uzmemo u obzir ova tri dnevnika, dodajući ih već 33 presavijenim, i odredimo nepoznati broj redaka koristeći formule za sum i n-ti član:
S n = n * (a 1 + a n ) / 2; a n = a 1 + d * (n - 1) =>
S n = n * (a 1 + a 1 + d * (n - 1)) / 2 = (2 * a 1 - d) / 2 * n + d * n 2/2
Poznate podatke zamjenjujemo posljednjom jednakošću i rješavamo dobivenu kvadratnu jednadžbu za n:
36 = 0.5 * n + 0.5 * n2 ili
n 2 + n - 72 = 0
Diskriminator: D = 1 - 4 * 1 * (-72) = 289
Korijeni: n = (-1 ± 17) / 2 = (8; -9)
Negativnu vrijednost odmah ćemo odbaciti, jer je u suprotnosti sa stanjem problema. Dakle, 8 redova piramide sadržavat će 36 logova. Budući da radnici nisu dovršili dva gornja reda, to znači da su samo zbrojili 6 redova trupaca.
Nekoliko riječi o napretku geometrijskog
Algebraika i geometrijska progresija, u pravilu, razmatraju se u okviru jedne teme, stoga je korisno dati ideju o drugom tipu uređenih serija brojeva. Dakle, geometrijska progresija je niz brojeva koji poštuju zakon:
a n = a n-l * r
To jest, za razliku od aritmetike, ovdje da bi dobili sve elemente, ne smijete dodati jedan broj, nego ga pomnožiti (r se naziva imenitelj).
Iz definicije je jasno da geometrijska progresija raste (smanjuje) mnogo brže od aritmetičke.
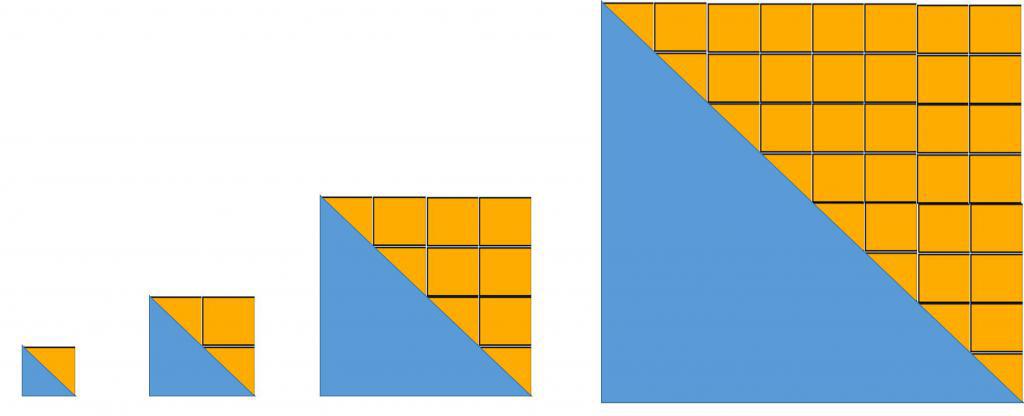
Često se koristi u geometriji, na primjer, pri izračunavanju površina figura koristeći njihovu podjelu na odvojene elemente (metoda dijeljenja na pola).