Blok dijagram: primjeri, elementi, konstrukcija. dijagrami toka

Ovaj će članak razmotriti primjere dijagrama toka koje možete naići u udžbenicima o računalnoj znanosti i drugoj literaturi. Dijagram toka je algoritam koji rješava sve zadatke koji su dodijeljeni programeru. Prvo trebate odgovoriti na pitanje što je algoritam, kako je grafički prikazan, i što je najvažnije, kako ga riješiti, znajući određene parametre. Treba odmah primijetiti da postoji nekoliko tipova algoritama.

Što je algoritam?

Tu je riječ upotrijebio matematičar Mohammed al-Khorezmi, koji je živio u razdoblju od 763-850. On je onaj koji je stvorio pravila za izvođenje aritmetičkih operacija (ima ih samo četiri). Ali GOST iz 1974. godine u kojem se navodi:

Algoritam je točan recept koji definira računski proces. Štoviše, postoji nekoliko varijabli s danim vrijednostima koje vode do izračuna do željenog rezultata.

Algoritam vam omogućuje da jasno odredite izvođača za izvođenje strogog slijed radnji riješiti problem i dobiti rezultat. Razvoj algoritma je razbijanje jednog velikog zadatka u određeni slijed koraka. Štoviše, programer algoritma mora znati sve značajke i pravila za njegovo stvaranje.

Značajke algoritma

Ukupno, postoji osam značajki algoritma (bez obzira na vrstu):

1. Postoji funkcija za unos početnih podataka.
2. Nakon završetka algoritma postoji zaključak određenog rezultata. Mora se imati na umu da je algoritam potreban za postizanje određenog cilja, naime, za dobivanje rezultata koji je izravno povezan s izvornim podacima.
3. Algoritam mora imati diskretnu strukturu tipa. Trebao bi biti prikazan u sekvencijalnim koracima. Štoviše, svaki sljedeći korak može započeti tek nakon završetka prethodnog.
4. Algoritam mora biti jednoznačan. Svaki je korak jasno definiran i ne dopušta proizvoljno tumačenje.
5. Algoritam mora biti konačan - potrebno ga je izvršiti u strogo određenom broju koraka.
6. Algoritam mora biti točan - tražiti samo pravo rješenje problema.
7. Zajednica (ili masovni karakter) - trebala bi raditi s različitim izvornim podacima.
8. Vrijeme potrebno za rješavanje algoritma treba biti minimalno. To određuje učinkovitost zadatka.

A sada, znajući koji algoritam postoje dijagrami toka, možete početi razmišljati o tome kako ih napisati. I to nije mnogo.

Usmeni zapis

Ovaj se obrazac obično koristi za opisivanje postupka za osobu: “Idi tamo, ne znam gdje. Donesi nešto, ne znam što.

Naravno, ovo je stripski oblik, ali suština je jasna. Primjerice, na primjer, uobičajeni zapis na prozorima autobusa: "U slučaju nesreće izvucite kabel, istisnite staklo".

Ovdje je uvjet jasno postavljen pod kojim se moraju izvoditi dvije akcije u strogom redoslijedu. No, to su najjednostavniji algoritmi, postoje složeniji algoritmi. Ponekad se koriste formule, posebne oznake, ali uz obvezni uvjet - izvođač mora sve razumjeti.

Dopušteno je mijenjati redoslijed radnji ako je potrebno vratiti se, primjerice, na prethodnu operaciju, ili zaobići neku naredbu pod određenim uvjetima. Istodobno, poželjno je brojati timove i navesti naredbu kojoj se odvija prijelaz: "Nakon što ste završili sve manipulacije, ponovite točke 3 do 5".

Snimanje u grafičkom obliku

Ovaj unos uključuje elemente dijagrama toka. Svi elementi su standardizirani, svaki tim ima određeni grafički zapis. Posebna naredba mora biti zabilježena unutar svakog bloka u običnom jeziku ili matematičkim formulama. Svi blokovi moraju biti povezani linijama - oni točno pokazuju koji red u izvršenim naredbama. Zapravo, ovaj tip algoritma prikladniji je za korištenje u programskom kodu, a ne u verbalnom.

Pisanje u programskim jezicima

U tom slučaju, ako je algoritam potreban da bi se zadatak riješio programom instaliranim na računalu, tada ga morate napisati posebnim kodom. Za to postoje mnogi programski jezici. Algoritam se u ovom slučaju naziva program.

dijagrami toka

Blok dijagram je prikaz algoritma u grafičkom obliku. Sve ekipe i akcije predstavljene su geometrijskim oblicima (blokovima). Unutar svake slike se uklapaju sve informacije o radnjama koje je potrebno izvršiti. Veze su prikazane kao normalne linije sa strelicama (ako je potrebno).

Za dizajn dijagrama toka algoritama postoji GOST 19.701-90. Opisuje postupak i pravila za njihovo kreiranje u grafičkom obliku, kao i osnovne metode rješavanja. U članku su prikazani glavni elementi dijagrama toka koji se koriste u rješavanju problema, primjerice u računalnoj znanosti. A sada razmotrimo pravila gradnje.

Osnovna pravila za izradu dijagrama toka

Postoje takve značajke koje svaki dijagram toka treba imati:

1. Mora postojati dva bloka - "Start" i "End". I u jednom primjerku.
2. Od početnog bloka do posljednje veze treba nacrtati.
3. Od svih blokova, osim posljednjeg, protočne linije bi trebale nestati.
4. Mora postojati numeracija svih blokova: od vrha do dna, s lijeva na desno. Redni broj treba biti smješten u gornjem lijevom kutu, čineći oznaku prekidom.
5. Svi blokovi moraju biti međusobno povezani linijama. Oni bi trebali odrediti redoslijed kojim se radnje izvode. Ako se protok kreće prema gore ili s desna na lijevo (drugim riječima, obrnutim redoslijedom), tada se izvlače strelice.
6. Linije su podijeljene na odlazne i dolazne. Treba napomenuti da je jedan redak za jedan blok, a za drugi dolazni.
7. Iz početnog bloka u shemi, linija protoka napušta samo budući da je prva.
8. Ali konačni blok ima samo ulaz. To je jasno prikazano u primjerima dijagrama toka koji su dostupni u članku.
9. Da bi vam bilo lakše čitati dijagrame toka, dolazne linije se izvlače odozgo, a odlazne linije odozdo.
10. Prisutnost praznina u protočnim crtama. Oni su nužno označeni posebnim konektorima.
11. Da bi se olakšao dijagram toka, dopušteno je pisati sve informacije u komentarima.

Grafički elementi dijagrama toka za rješavanje algoritama prikazani su u tablici:

Algoritmi linearnog tipa

To je najjednostavniji oblik, koji se sastoji od određenog slijeda radnji, ne ovisi o tome koji se podaci unose na početku. Postoji nekoliko naredbi koje se izvršavaju jednom i samo nakon prethodnog. Linearni blok dijagram izgleda ovako:

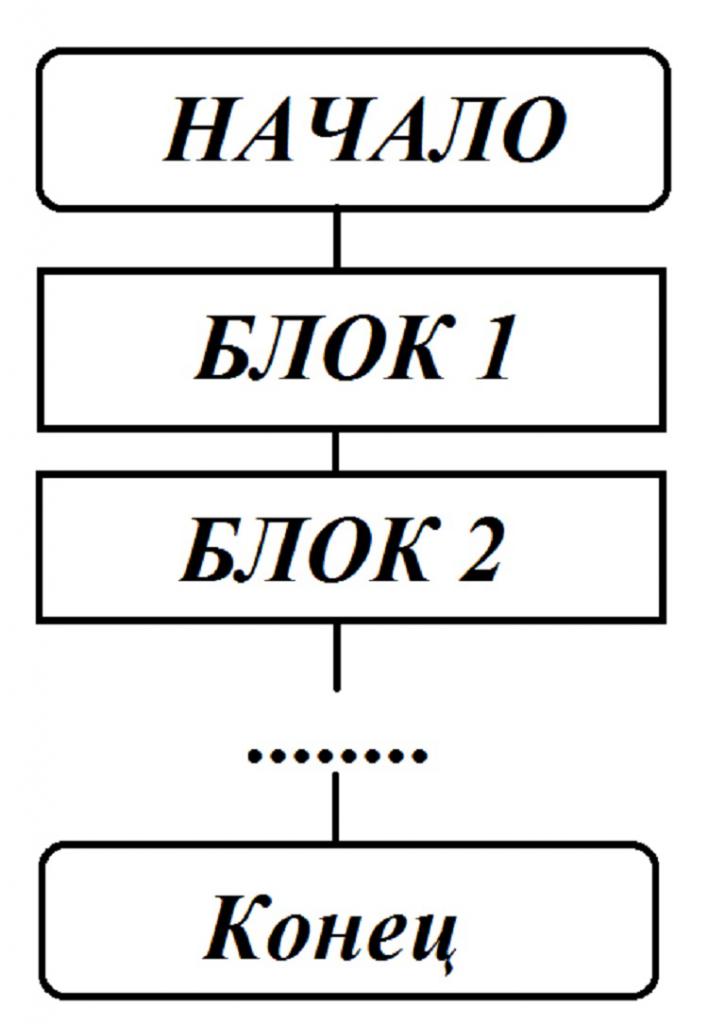
Štoviše, veze mogu ići odozgo prema dolje i s lijeva na desno. Takav dijagram toka koristi se za pisanje algoritama izračuna pomoću jednostavnih formula koje nemaju ograničenja na vrijednosti varijabli uključenih u formule za izračun. Linearni algoritam sastavni je dio složenih proračunskih procesa.

Algoritmi grananja

Dijagrami toka temeljeni na takvim algoritmima su složeniji od linearnih. Ali bit se ne mijenja. Algoritam grananja je proces u kojem daljnje djelovanje ovisi o tome kako je uvjet ispunjen i koje je rješenje dobiveno. Svaki pravac djelovanja je grana.

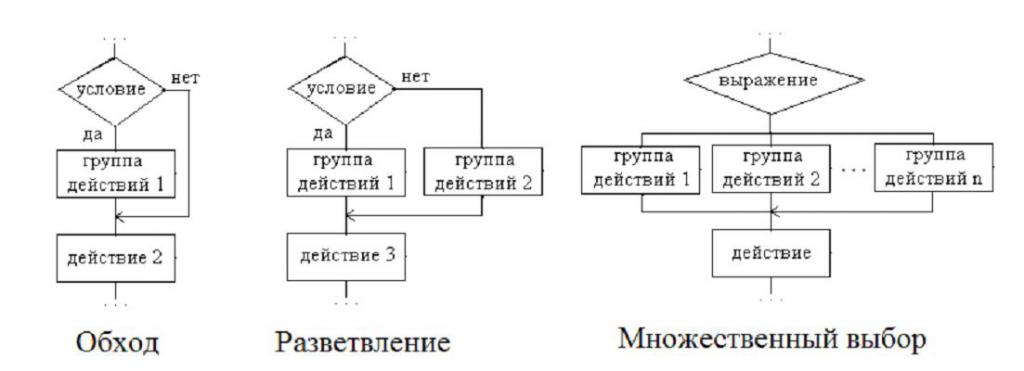
Dijagrami prikazuju blokove koji se nazivaju "Rješenje". Ima dva izlaza, a unutra se zapisuje logički uvjet. Od toga ovisi kako će se izvršiti daljnje kretanje u shemi algoritma. Možete podijeliti algoritme grananja na tri skupine:

1. "Obilaznica" - dok jedna od grana nema operatera. Drugim riječima, zaobilazi se nekoliko radnji druge grane.
2. "Grananje" - svaka grana ima određeni niz izvedenih akcija.
3. "Višestruki izbor" je vilica u kojoj postoji nekoliko grana i svaka sadrži određeni skup radnji koje treba izvršiti. I tu je jedna značajka - izbor smjera izravno ovisi o tome koje su vrijednosti dane za izraze uključene u algoritam.

To su jednostavni algoritmi koji se rješavaju vrlo jednostavno. Prijeđimo sada na složenije.

Ciklički algoritam

Ovdje je sve vrlo jasno - ciklički blok dijagram predstavlja algoritam u kojem se homogeni izračuni ponavljaju mnogo puta. Po definiciji, ciklus je specifičan slijed svih radnji koje se izvode više puta (više od jednom). Postoji nekoliko vrsta ciklusa:

1. Tko zna broj ponavljanja akcija (oni se nazivaju i ciklusi s brojačem).
2. U kojem je broj ponavljanja nepoznat - s post-uvjetom i preduvjetom.

Bez obzira na to koji se tip ciklusa koristi za rješavanje algoritma, on mora imati varijablu s kojom se pojavljuje izlaz. Određuje broj ponavljanja ciklusa. Radni dio (tijelo) ciklusa je specifičan slijed radnji koji se izvodi na svakom koraku. Sada ćemo pobliže razmotriti sve vrste ciklusa koji se mogu pojaviti pri izradi algoritama i rješavanju problema računalne znanosti.

Brojčani ciklusi

Na slici je prikazan jednostavan blok dijagram u kojem postoji ciklus s brojačem. Ovaj tip algoritma pokazuje da je broj ponavljanja određenog ciklusa unaprijed poznat. I ovaj broj je fiksan. U ovom slučaju, varijabla koja broji broj koraka (ponavljanja) naziva se brojač. Ponekad se u udžbenicima mogu susresti i druge definicije - parametar ciklusa, kontrolna varijabla.

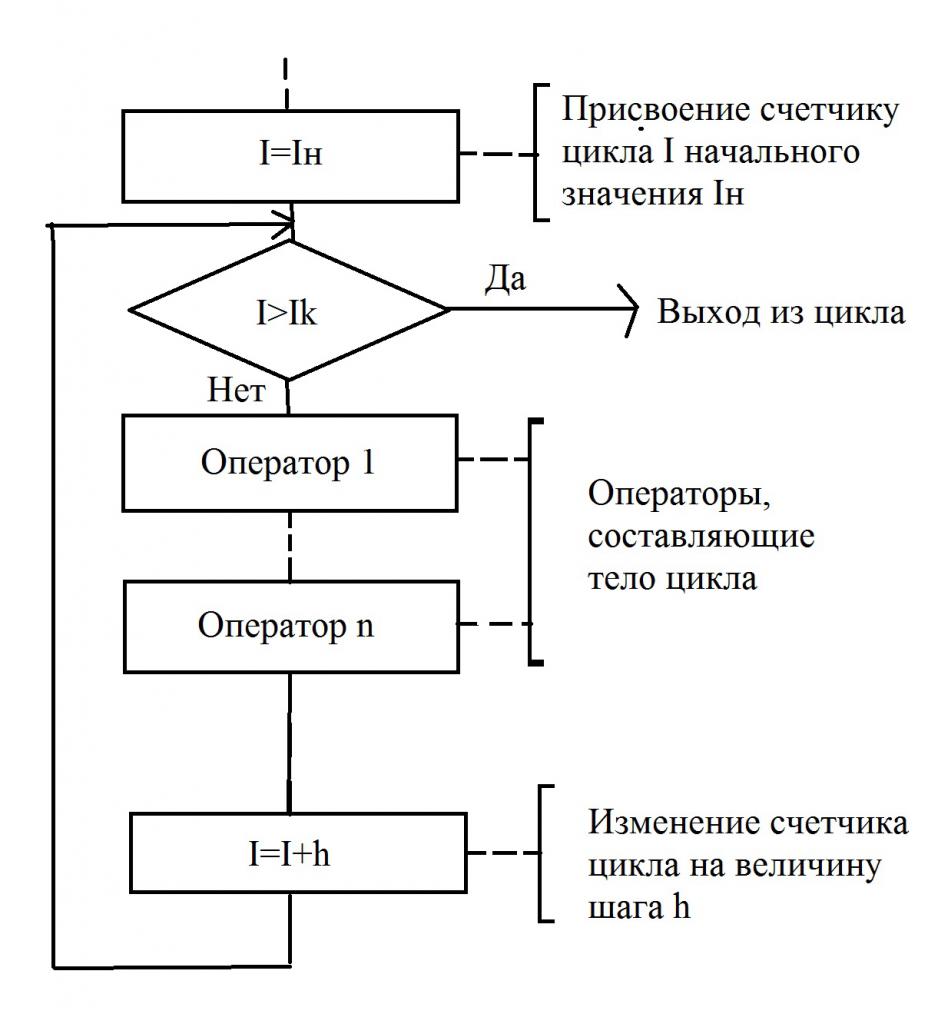
Blok dijagram vrlo slikovito prikazuje kako petlja funkcionira s brojačem. Prije nego što nastavite s prvim korakom, morate dodijeliti početnu vrijednost brojaču - to može biti bilo koji broj, to ovisi o specifičnom algoritmu. U slučaju kada je konačna vrijednost manja od vrijednosti brojača, izvršit će se određena skupina naredbi koje čine tijelo petlje.

Nakon što je tijelo izvršeno, brojač se mijenja za vrijednost inkrementa brojača, označenu slovom h. U slučaju da je dobivena vrijednost manja od konačne, ciklus će se nastaviti. I završit će se samo kada je konačna vrijednost manja od brojača petlje. Samo u tom slučaju izvršit će se radnja koja slijedi ciklus.

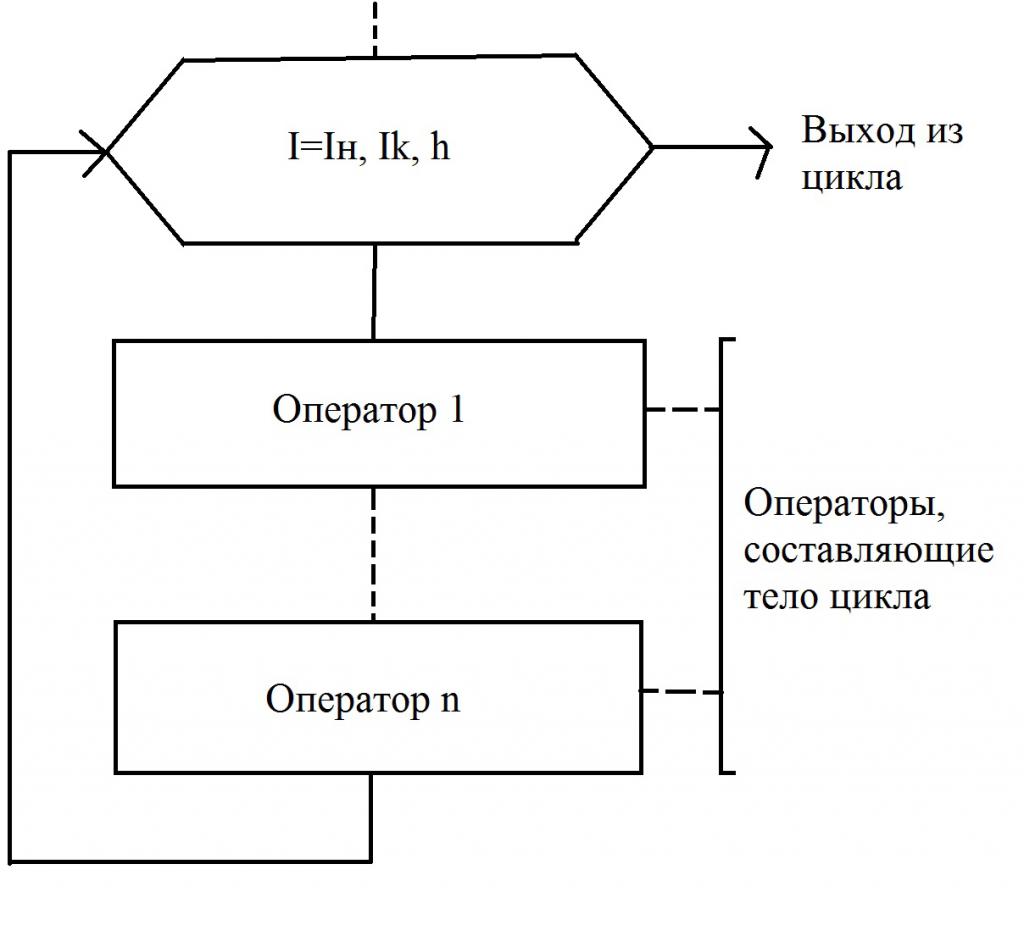
Tipično, blok koji se naziva "Priprema" koristi se u notaciji blok-dijagrama. Upisuje se u brojač, a zatim se prikazuju sljedeći podaci: početna i konačna vrijednost, korak promjene. U blok dijagramu to su parametri I n, Ik i h. U slučaju kada je h = 1, veličina koraka nije zabilježena. U drugim slučajevima, to se mora učiniti. Neophodno je pridržavati se jednostavnog pravila - ulazna linija treba ulaziti odozgo. A streamline koji ide ispod (ili desno, ovisno o specifičnom algoritmu) trebao bi pokazati prijelaz na sljedećeg operatora.

Sada ste u potpunosti proučili opis dijagrama toka prikazanog na slici. Možete nastaviti s daljnjim proučavanjem. Kada se koristi ciklus s brojačem, moraju biti ispunjeni određeni uvjeti:

1. Tijelu nije dopušteno mijenjati (prisilno) vrijednost brojača.
2. Zabranjeno je prijenos kontrole izvana prema operateru tijela. Drugim riječima, u ciklus se može ući samo od samog početka.

Preduslovi ciklusa

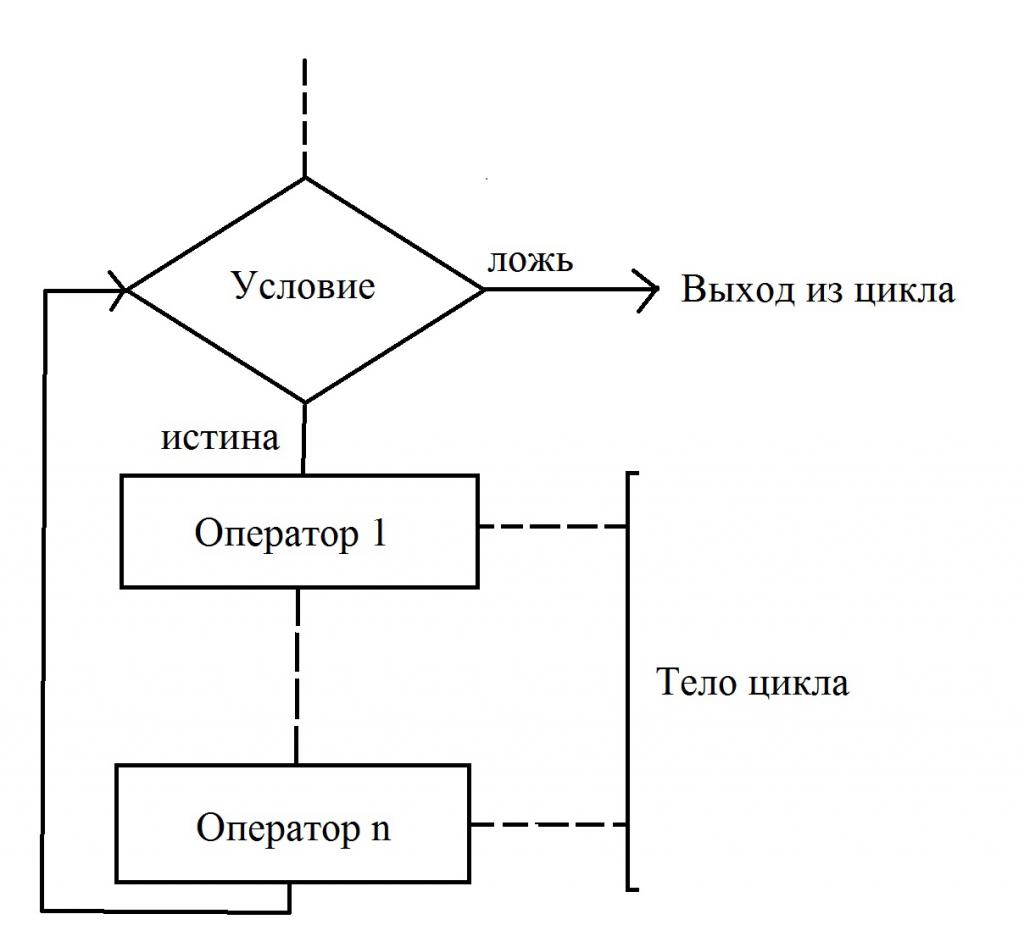
Ova vrsta ciklusa koristi se u slučajevima kada broj ponavljanja nije unaprijed poznat. Ciklus s preduvjetom je tip algoritma u kojem, neposredno prije početka rada tijela, provjerava stanje pod kojim je dopušten prijelaz na sljedeću radnju. Primijetite kako su prikazani elementi blok-dijagrama.

U slučaju kada je uvjet zadovoljen (izjava je istinita), dolazi do prijelaza na početak tijela ciklusa. On izravno mijenja vrijednost najmanje jedne varijable koja utječe na vrijednost skupa uvjeta. Ako se ne pridržavate ovog pravila, dobivamo "petlju". U slučaju da se nakon sljedeće provjere stanja izvršenja tijela petlje, ispostavi da je lažna, tada dolazi do izlaza.

U dijagramima toka algoritama dopušteno je provjeravati ne istinu, nego lažnost početnog stanja. U tom slučaju, ciklus će izaći samo ako je vrijednost uvjeta istinita. Obje opcije su točne, njihova upotreba ovisi o tome što je konkretno prikladnije koristiti za rješavanje određenog problema. Ova vrsta ciklusa ima jednu značajku - tijelo se ne može izvršiti kada je uvjet lažno ili istinito (ovisno o varijanti koja se koristi za rješavanje algoritma).

U nastavku je dijagram toka koji opisuje sve ove radnje:

Što je ciklus s post-uvjetom?

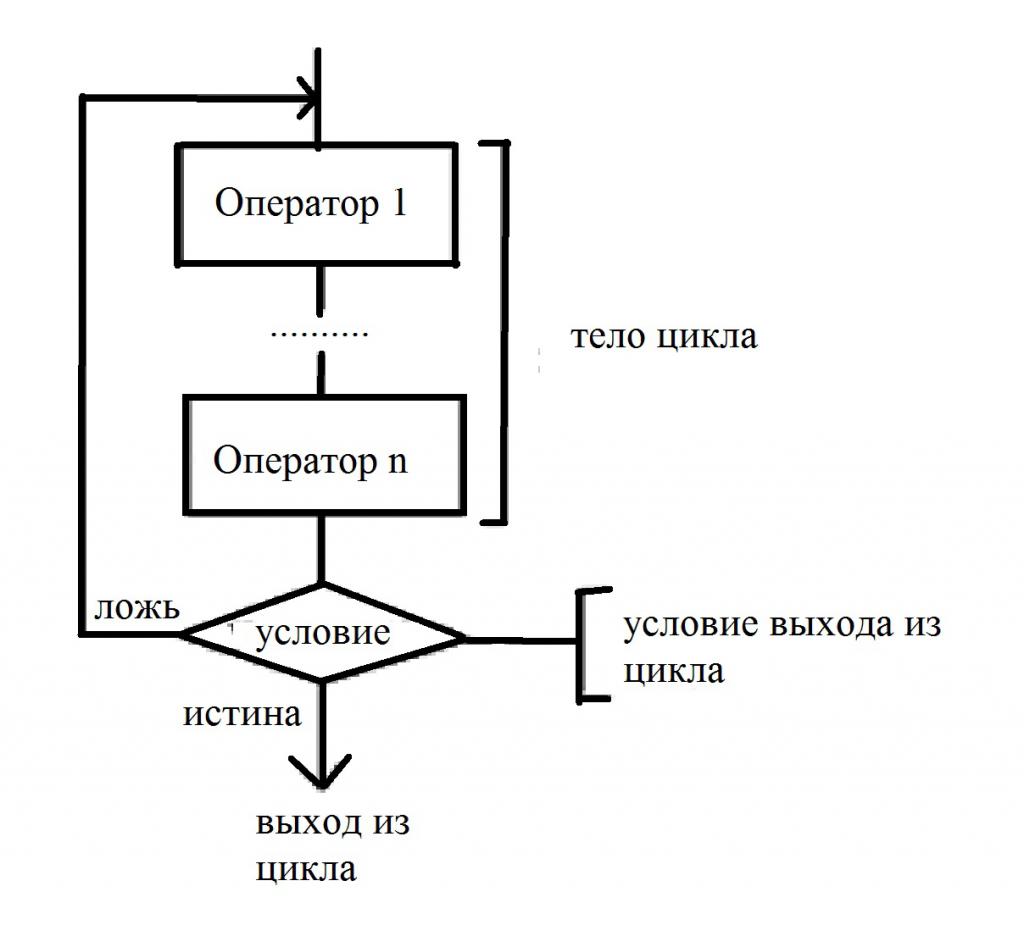
Ako bolje pogledate, onda je ova vrsta ciklusa donekle slična prethodnoj. Pokušat ćemo sami izraditi dijagram toka koji opisuje ovaj ciklus. Posebnost je u tome što broj ponavljanja nije unaprijed poznat. A stanje se postavlja nakon povlačenja iz tijela. To pokazuje da će tijelo, bez obzira na odluku, biti izvršeno barem jednom. Radi jasnoće, pogledajte dijagram toka koji opisuje stanje i izjave:

Ne postoji ništa teško u konstrukciji algoritama s ciklusima, dovoljno je da ih razumijemo samo jednom. A sada se okrećemo složenijim strukturama.

Složeni ciklusi

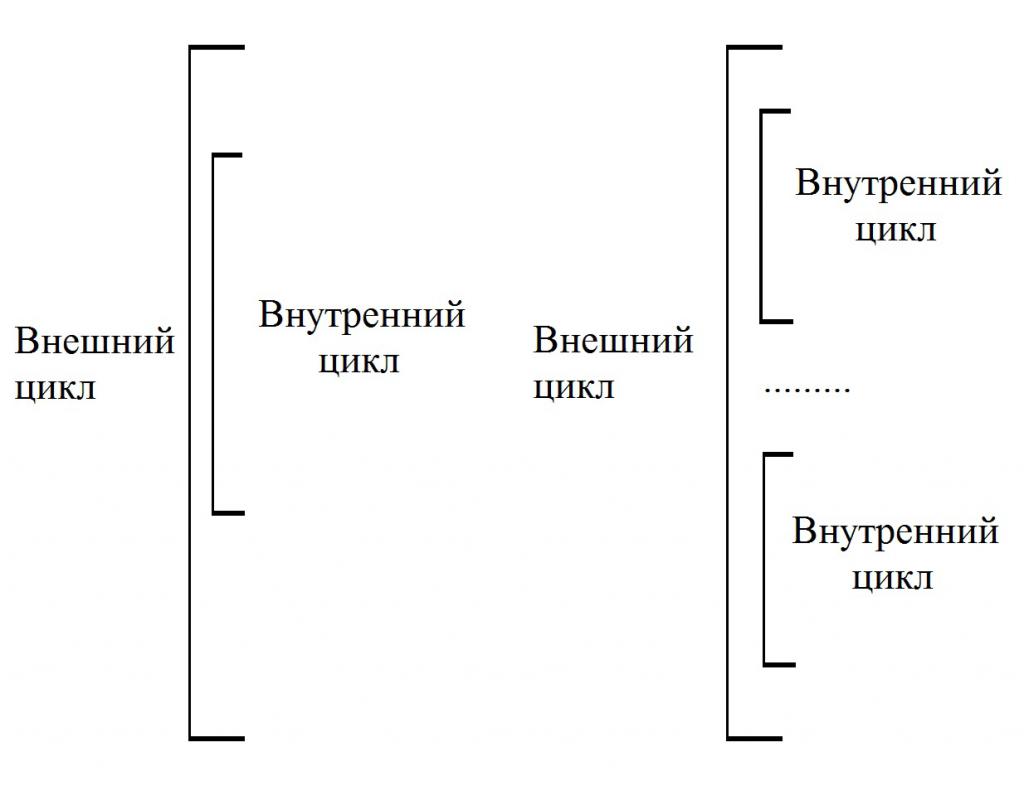
Kompleksne su one konstrukcije unutar kojih postoji jedan ili više jednostavnih ciklusa. Ponekad se nazivaju ugniježđena. Istovremeno, one strukture koje pokrivaju druge cikluse nazivaju se "vanjskim". A oni koji su uključeni u dizajn vanjskih - unutarnjih. Kada se izvodi svaki korak vanjske petlje, unutarnja petlja se potpuno pomiče, kao što je prikazano na slici:

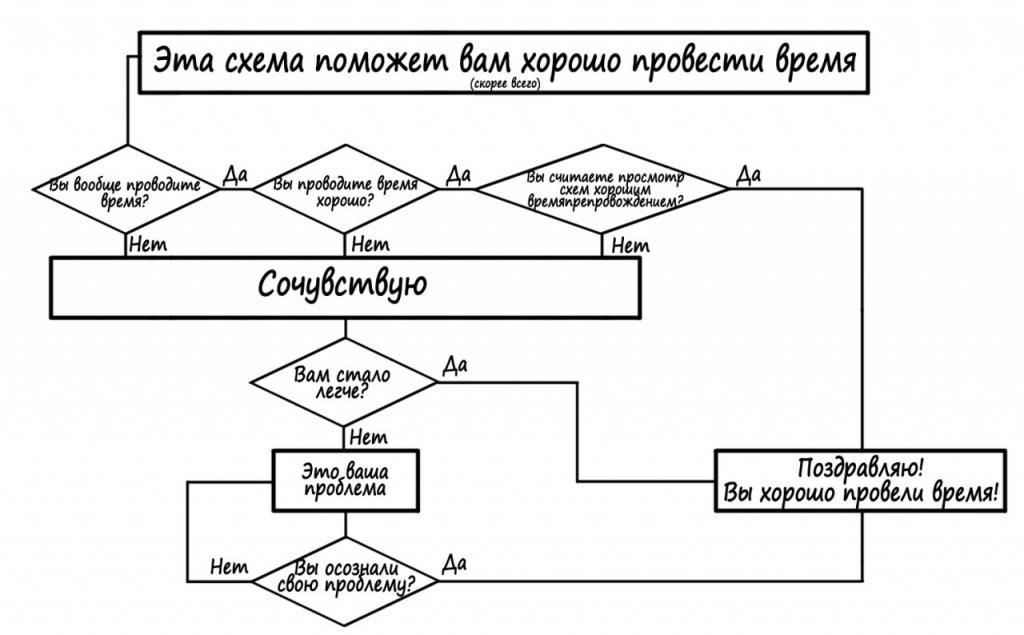
To je sve, vi pregledali glavne značajke izgradnje dijagrama toka za rješavanje algoritama, znate principe i pravila. Sada možete razmotriti konkretne primjere dijagrama toka iz života. Primjerice, u psihologiji se takve konstrukcije koriste kako bi osoba odlučila pitanje:

Ili primjer iz biologije za rješavanje problema:

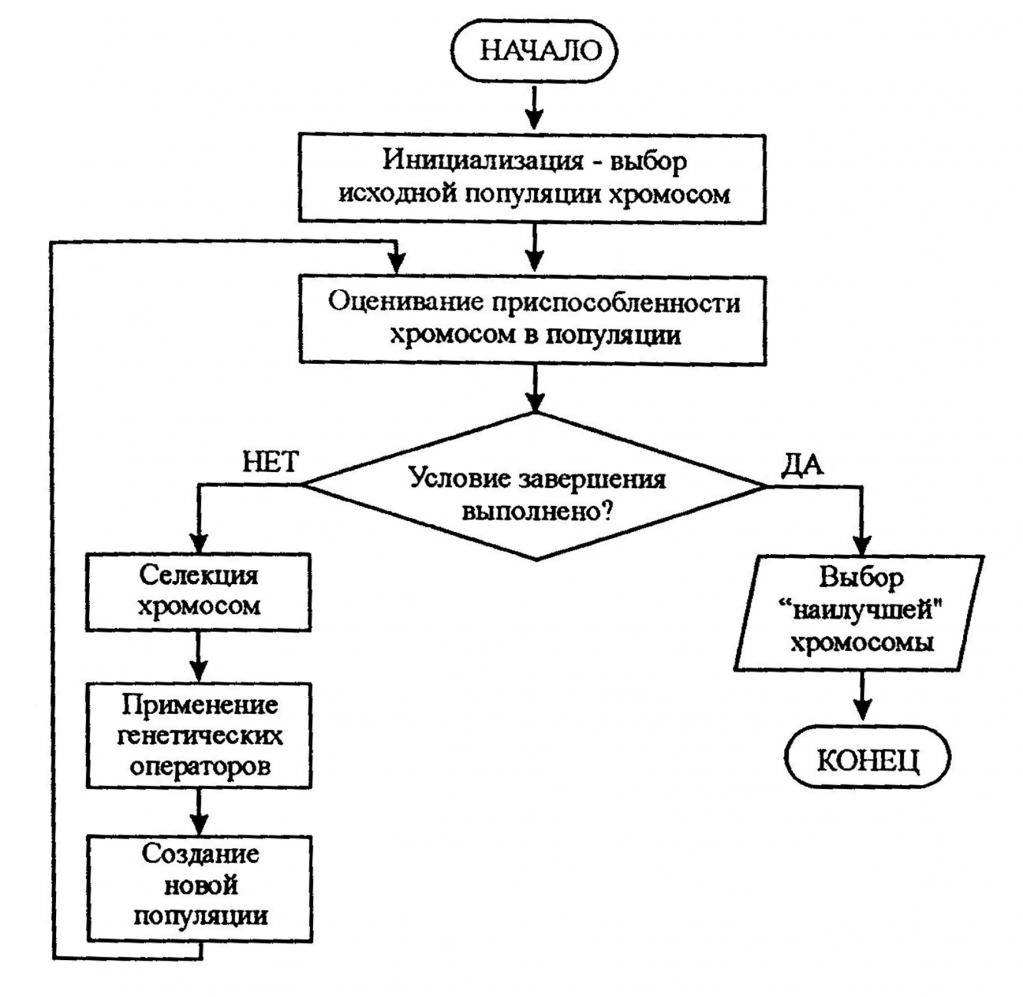
Rješavanje problema s dijagramima toka

Sada ćemo pogledati primjere problema s dijagramima toka koji se mogu naći u udžbenicima informatike. Na primjer, dat je blok dijagram prema kojem je riješen neki algoritam:

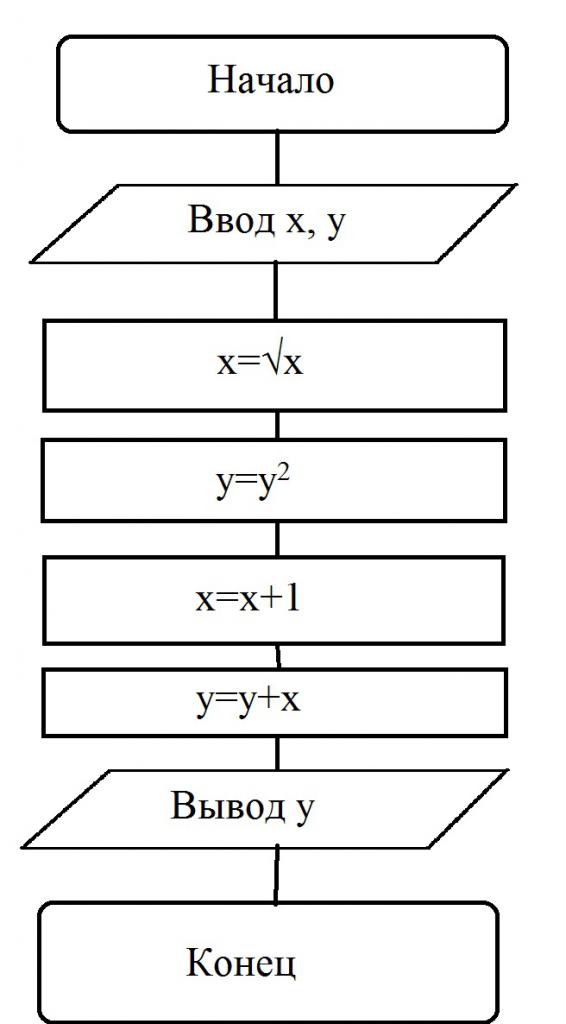
U tom slučaju korisnik samostalno unosi vrijednosti varijabli. Pretpostavimo da je x = 16, a y = 2. Postupak:

1. Unose se vrijednosti x i y.
2. Postupak pretvorbe se izvodi: x = =16 = 4.
3. Uvjet je ispunjen: y = y ² = 4.
4. Izračun se izvodi: x = (x + 1) = (4 + 1) = 5.
5. Sljedeća se varijabla dalje izračunava: y = (y + x) = (5 + 4) = 9.
6. Prikazano je rješenje: y = 9.

U ovom primjeru dijagrami toka za računalnu znanost jasno pokazuju kako je algoritam riješen. Morate obratiti pozornost na činjenicu da su vrijednosti x i y postavljene u početnoj fazi i da mogu biti bilo što.