Boolean izraz: izgradnja i pojednostavljenje
Glavni zadatak logike je utvrditi je li izjava netočna ili se može smatrati istinitom. Za to je izumljeno nekoliko metoda. Razvijeni načini određivanja istina je ili lažno, na temelju drugih iskaza i njihovih atributa. Boolean izraz - baza pojam znanosti i njegovi parametri određuju koje se operacije mogu izvesti.
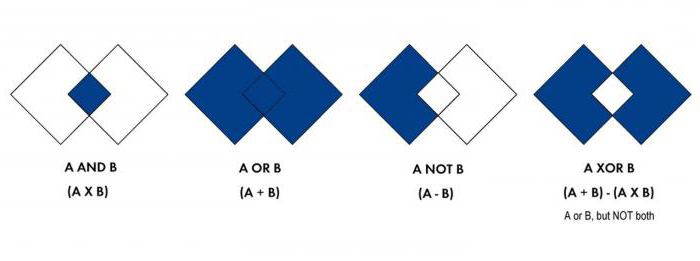
Opći uvjeti
Danas se logika proučava u obliku matematičke logike. Ona se temelji isključivo na formalnim metodama spoznaje. Jedan od ključnih dijelova smjera je algebra logike. Specijalizirana je samo u složenim objektima i metodama koje omogućuju postavljanje njihovih parametara. Koristili su strogo algebarske načine učenja.
Znanost se naziva Booleova algebra, budući da je njezin autor George Boole, svoje glavne ideje formulirao je 1854. godine, kada je objavio temeljnu knjigu. Boule je sebi postavio zadatak da prouči operacije na temelju kojih funkcionira ljudski um, da razumije mehanizam rasuđivanja, da ga opiše simbolima. Postigavši taj uspjeh, uspio je stvoriti novu znanost.
Logički izrazi u programiranju
Uvjetni logički izraz su neke varijable i konstante koje su klasificirane kao jednostavne. Svi se objekti međusobno kombiniraju usporedbom. . Kao rezultat izračuna moguće je dobiti neki konačni uvjetni izraz: true ili false .
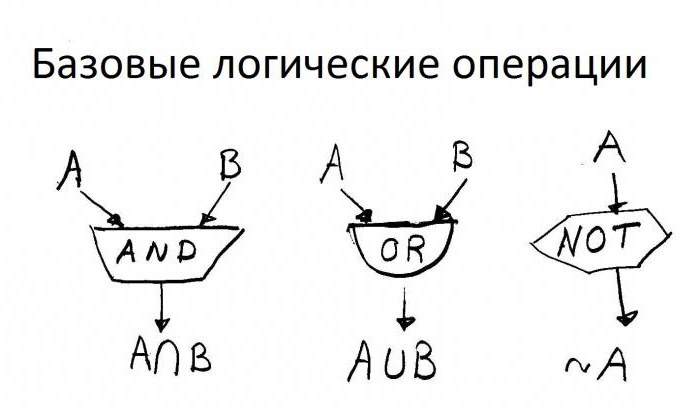
Najprimjenjivija logika u programiranju. Na primjeru Pascala možemo izdvojiti najvažnije operacije koje se koriste u praksi:
- definicija većeg od ta dva;
- definicija manjeg od ta dva;
- izračun manje ili jednako;
- izračun veći ili jednaki;
- definicija jednakosti dvaju izraza;
- zaključak da izrazi nisu jednaki.
Ako je tijekom programiranja potrebno konstruirati logički izraz, ali se stvarni brojevi međusobno uspoređuju, treba uzeti u obzir sljedeću činjenicu: prikaz brojeva je netočan jer je potrebno zaokruživanje. To znači da rad računanja stroge jednakosti ne može biti točan. Iskusni programeri preporučuju izbjegavanje pristupa ovoj operaciji ako je moguće, budući da je vjerojatno da će se jednakost na kraju smatrati netočnom, a da nije takva.
Primjer: x = (2,23 * x / 2,23)
Slažem se, istina formule je vidljiva. No, kada ga pišemo u računalni kôd i neizbježnost greške zaokruživanja u kalkulacijama, to će biti netočno.
Još jedna suptilna točka: uvjetni logički izraz nužno je napisan u zagradama ako je to operand. Pravilo proizlazi iz razvijene hijerarhije operacija. Na primjer, usporedba u njenom prioritetu je niža od drugih, a logičke operacije su visoke. . Da bi se promijenio proces izračunavanja konkretnog primjera s obzirom na takvu narudžbu, potrebno je postaviti zagrade .
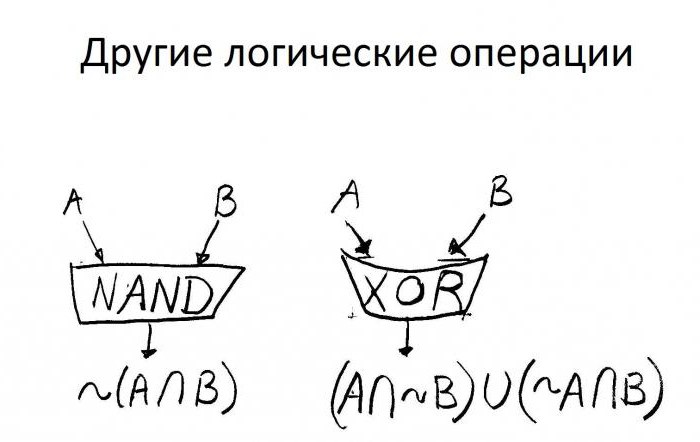
Osnove znanosti
Objekt u logici obično se shvaća kao naracija koja je točno prijavljena da je to laž, istina. Vrijednost logičkog izraza, kada je istinita, zapisana je kao jedna, druga opcija označena je nulom.
Pod logičkim operacijama, uobičajeno se shvaćaju takva djelovanja (u pravilu, proces razmišljanja), koji u konačnici daju povećanje znanja, a također vode do stvaranja potpuno novih objekata.
Logičan izraz je usmeni, možete ga zapisati. Uključen je u objekte zajedno s konstantama. Izraz izravno ovisi o varijablama objekata i postaje ili jedna ili nula.
Ako ste se morali nositi sa složenim izrazom, morate zapamtiti da on uključuje složene jednostavne izraze, za povezivanje čije su logičke operacije korištene.
Logika identificira ključne operacije koje se nazivaju:
- zajedno;
- ekvivalencija;
- odvajanje;
- implikacija;
- inverzija.
. Riješiti gotovo svaki njihov primjer bit će dovoljan .
veznik
Taj se pojam obično shvaća kao takva složena operacija, koja može biti istinita samo ako su obje jednostavne komponente istinite. Ostale opcije smatraju se netočnima.
Napisano je kao: F = A & B.
Tablica:
| B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 0 |
razdvajanje
U ovoj situaciji, istina logičkih izraza određuje se na temelju analize vrijednosti (jedne i nule) komponenti jednostavnih izraza. Ako su obje lažne, tada funkcija ima i vrijednost nula. Inače, njegova vrijednost je jedna.
Upisuje se kao: F = A + B.
Tablica:
| B | F |
1 | 1 | 1 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 0 |
inverzija
Pojam se odnosi na operaciju kada se pretvori u lažni izraz koji je ranije bio istinit, i obrnuto. Ako je izvorni objekt ispravan, rezultat je lažan, a ako je u početku postojala laž, ona se pretvara u istinu.
Tablica:
| Nea |
1 | 0 |
0 | 1 |
ekvivalencija
Ovaj logički izraz će značiti samo jedan kada oba izraza u primjeru znače istu stvar.
Tablica:
| B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
upletenost
Pojam se primjenjuje na tako složen izraz logike koji je lažan ako lažno slijedi iz istine. Druge situacije: vrijednost je jednaka jednoj. Operacija se primjenjuje na dva jednostavna objekta, od kojih se jedan zove uvjet, a drugi je posljedica.
Tablica:
| B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 1 |
0 | 0 | 1 |
Operacije: logičke nijanse
Znajući što se logički izraz koristi kao objekt, možete ispravno izračunati rezultat. Istovremeno, treba imati na umu da su operacije u logici, kao u aritmetici, one operacije koje su potrebne za interakciju s brojevima. . Logičke operacije pomažu u izgradnji logičkih izraza - to je također paralela s algebrom .
Kao dio logičkih izraza su konstante i varijable. Prvi ima određenu vrijednost - nulu ili jednu. Ako izraz sadrži neke varijable, time će postaviti boolean funkciju, čija se vrijednost izračunava na temelju argumenata. Vrijednosti argumenata za svaki zadatak su specificirane u uvjetima. Vi samo trebate ih zamijeniti u izrazu, a zatim provesti daljnji izračun.
Svaki logički izraz može imati vlastitu tablicu istine, to jest objekt koji detaljno opisuje sve varijacije koje vrijednosti i kada funkcija prihvaća ako se koristi određeni skup varijabli. Jedan redak takve tablice je jedan skup početnih uvjeta za izračun. . Ako su u funkciju uključene N varijable, tada je dvostruko više redaka .
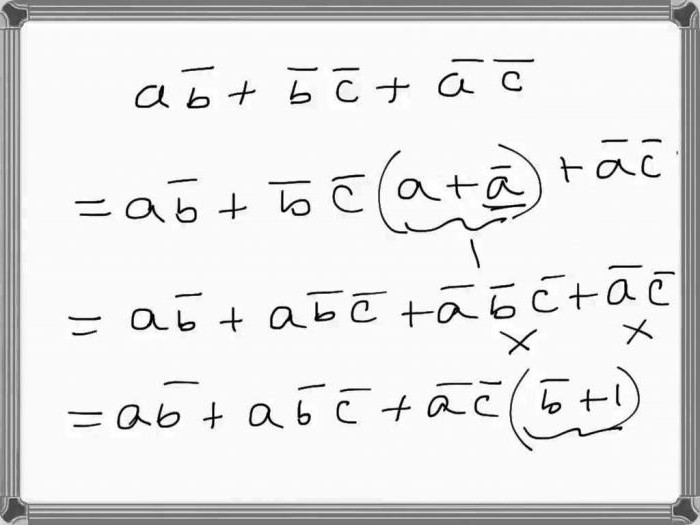
Tablice istine
Za svaku tablicu postoje sljedeća opća svojstva:
- broj već spomenutih linija, dvostruko veći broj varijabli;
- Broj stupaca u tablici je jedan više od broja uključenih varijabli.
Bez obzira na to što je skup vrijednosti varijabli danih u stanju, uvijek se može formulirati izraz koji će biti jednak jednom na određenom skupu varijabli.
Zapisuje se kao "disjunkcija veznika". U praksi to znači da možete izgraditi određeni izraz, da imate pred sobom spreman stol za istinu. Naravno, volumen ove tablice može znatno zakomplicirati zadatak matematike.
pojednostaviti
Često postoje situacije kada matematički izraz zahtijeva pojednostavljenje za adekvatnost rješenja. Postoje određene pretvorbe koje su primjenjive u Booleovoj logici.
Konkretno, jedan izraz može se zamijeniti drugim, što je ekvivalentno. Provjerite ekvivalentnost analizirajući tablice istine. Ako se podudaraju, možete ih zamijeniti. . Ovdje stupa na snagu lažno pravilo, kada se u objektu A promijeni u neki subexpresion P, koji je bio prisutan ovdje prije Q, a dobiva se izraz B. Po svim izračunima to je ekvivalentno A.

Pojednostavljenje logičkih izraza obično se naziva minimizacija. Glavni zadatak minimizacije je predstavljanje funkcije u takvom obliku, kada su slova, operacije, najmanji mogući broj. Možete postići jednu od dvije opcije:
- algebarski;
- grafički.
Algebarska metoda
Logički izraz može se pojednostaviti algebarskom metodom pojednostavljenjem formule. To se postiže ekvivalentnim transformacijama koje su već opisane. U ovom slučaju, potrebno je uzeti u obzir identitete i pravila koja postoje u Booleovoj algebri.
Pojednostavljeni izraz od onoga koji se u početku morao riješiti, razlikuje se prvenstveno brojem slova. Međutim, često postoje problemi kada morate dokazati ekvivalentnost izvornog izraza i rezultirajuće pojednostavljenje. To se radi usporedbom tablica istine.
Ako primjer prikazuje elementarne izjave, možete ih mijenjati, ne samo općim pravilima, nego i onima koji se odnose na operacije na skupovima.
Prilikom analize izjava koje se odnose na skupove, često je najbolja opcija smanjiti izraze na implikacije, kada članovi više ne sadrže implikacije.