Centripetalno ubrzanje - izlazna formula i praktična primjena

Centripetalno ubrzanje nas prati posvuda. To čini naše Zemlja se okreće oko sunca. Rezultirajuća gravitacija omogućuje nam da postojimo na ovom planetu. Kako možemo razumjeti što je centripetalno ubrzanje? Definicija ove fizikalne veličine prikazana je u nastavku.

zapažanja

Najjednostavniji primjer ubrzanja tijela koje se kreće u krugu može se promatrati rotiranjem kamena na užetu. Povučeš konopac i konopac povlači kamen u središte. U svakom trenutku, konopac govori kamenu određenu količinu pokreta, i svaki put - u novom smjeru. Možete zamisliti kretanje užeta u obliku niza slabih trzaja. Trzaj - i konop mijenja smjer, drugi kreten - još jedna promjena, i tako dalje u krug. Ako iznenada otpustite uže, kreteni će se zaustaviti i zajedno s njima zaustaviti će se promjena smjera brzine. Kamen će se pomaknuti u smjeru tangente na krug. Postavlja se pitanje: "S kojim će se ubrzanjem tijelo pomaknuti u ovom trenutku?"

Centripetalna formula ubrzanja

Prije svega, valja napomenuti da je kretanje tijela u krugu teško. Kamen istodobno sudjeluje u dva tipa kretanja: pod djelovanjem sile, kreće se prema središtu rotacije, a istovremeno tangencijalno prema krugu, udaljava se od tog središta. Prema Newtonovom drugom zakonu, sila koja drži kamen na užetu usmjerena je prema središtu rotacije duž tog užeta. Također će se usmjeriti na vektor ubrzanja.

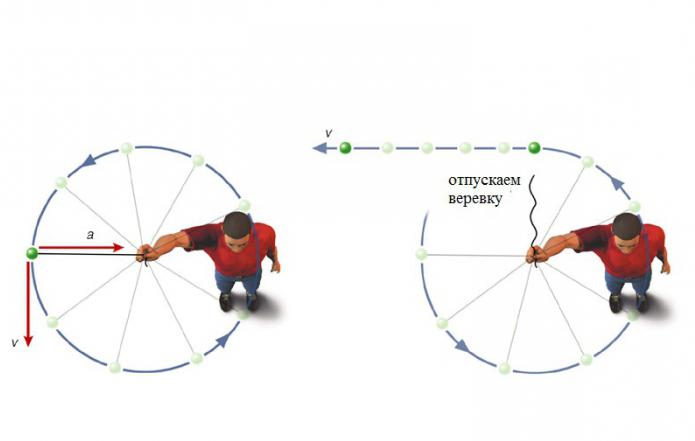
Neka neko vrijeme naš kamen, krećući se ravnomjerno brzinom V, dođe iz točke A u točku B. Pretpostavimo da je u trenutku kada je tijelo prešlo točku B centripetalna sila prestala djelovati na nju. Tada bi za neko vrijeme padala na točku K. Leži na tangenti. Ako bi u istom trenutku na tijelo djelovale samo centripetalne sile, tada bi se tijekom vremena t, kretanjem s istim ubrzanjem, pojavilo u točki O, koja se nalazi na ravnoj liniji, koja predstavlja promjer kruga. Oba segmenta su vektori i poštuju pravilo vektora. Kao rezultat zbrajanja tih dvaju kretanja u vremenskom intervalu t dobivamo rezultirajuće kretanje duž luka AB.

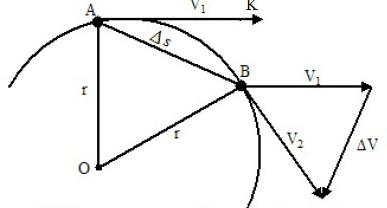
Ako se vremenski interval t smatra zanemarivim, tada se luk AB malo razlikuje od AB akorda. Prema tome, moguće je zamijeniti kretanje duž luka uz pomicanje duž tetive. U ovom slučaju, pomicanje kamena duž tetive će se pridržavati zakonitosti pravocrtnog kretanja, tj. Prijeđena udaljenost AB bit će jednaka proizvodu brzine kamena u vrijeme njegova kretanja. AB = V x t.

Označite željeno centripetalno ubrzanje slovom a. Tada se put koji pokriva samo djelovanje centripetalnog ubrzanja može izračunati pomoću formule jednoliko ubrzanog gibanja:

AO = na 2/2.

Udaljenost AB jednaka je brzini i vremenu, tj. AB = V x t,

AO - prethodno izračunata pomoću formule ravnomjerno ubrzano kretanje za kretanje u ravnoj liniji: AO = na 2/2.

Zamjenjujući ove podatke u formulu i pretvarajući ih, dobivamo jednostavnu i elegantnu centripetalnu formulu ubrzanja:

a = v ² / R

To se može izraziti riječima na sljedeći način: centripetalno ubrzanje tijela koje se kreće u krugu jednako je kvocijentu dijeljenja linearne brzine kvadrirane radijusom kruga u kojem se tijelo okreće. Centripetalna sila u ovom slučaju će izgledati kao slika ispod.

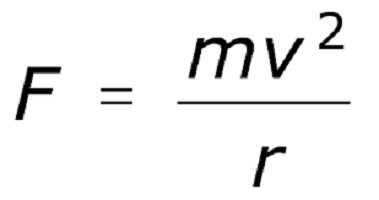
Kutna brzina

Kutna brzina jednak količniku linearne brzine podijeljen s radijusom kruga. Isto je i obratno: V = ωR, gdje je ω kutna brzina

Ako zamijenite ovu vrijednost u formuli, možete dobiti izraz centrifugalnog ubrzanja za kutnu brzinu. Izgledat će ovako:

a = ω ² R.

Ubrzanje bez promjene brzine

Pa ipak, zašto se tijelo s ubrzanjem usmjerenim prema središtu ne kreće brže i ne približava se središtu rotacije? Odgovor leži u samoj formulaciji ubrzanja. Činjenice ukazuju na to da je vožnja u krugu stvarna, ali da bi se održala, potrebno je ubrzanje usmjereno prema središtu. Pod djelovanjem sile uzrokovane ovim ubrzanjem dolazi do promjene količine gibanja, zbog čega se putanja gibanja stalno savija, mijenjajući smjer vektora brzine cijelo vrijeme, ali ne mijenjajući njegovu apsolutnu vrijednost. Krećući se u krugu, naš strastveni kamen ulazi u unutrašnjost, inače bi se nastavio kretati po tangenti. Svaki trenutak vremena, ostavljajući na tangenti, kamen privlači središte, ali ne upada u njega. Drugi primjer centripetalnog ubrzanja može biti skijaš na vodi, opisujući male krugove na vodi. Slika sportaša je nagnuta; čini se da pada, nastavljajući se kretati i naginjati se naprijed.

Stoga možemo zaključiti da ubrzanje ne povećava brzinu tijela, jer su vektori brzine i ubrzanja okomiti jedan na drugi. Dodajući vektor brzine, ubrzanje samo mijenja smjer kretanja i drži tijelo u orbiti.

Višak sigurnosne granice

U dosadašnjem iskustvu bavili smo se idealnim konopcem koji nije bio poderan. No, recimo, naš konopac je najčešći i čak možete izračunati silu, nakon čega će se jednostavno slomiti. Da bi se izračunala ta sila, dovoljno je usporediti sigurnosnu granicu užeta s opterećenjem koje doživljava u procesu rotacije kamena. Okretanjem kamena bržom brzinom, dajete joj više pokreta, što znači više ubrzanja.

S promjerom uže od jute od oko 20 mm, njegova vlačna čvrstoća je oko 26 kN. Važno je napomenuti da se dužina užeta ne pojavljuje nigdje. Okretanjem tereta veličine 1 kg na užetu s radijusom od 1 m, može se izračunati da je linearna brzina potrebna za lom je 26 x 10 ³ = 1 kg x V 2/1 m. Dakle, brzina koja je opasna za prekoračenje jednaka je 26 x 10 ³ = 161 m / s.

gravitacija

Pri razmatranju iskustva zanemarili smo akciju sila gravitacije, budući da je pri tako visokim brzinama njegov utjecaj zanemariv. Ali možete vidjeti da kada odmotavanje dugačkog užeta tijelo opisuje složeniju putanju i postupno se približava tlu.

Nebeska tijela

Ako prenesemo zakone kretanja duž kruga u prostor i primijenimo ih na gibanje nebeska tijela Možete ponovno otvoriti nekoliko poznatih formula. Na primjer, sila kojom tijelo privlači Zemlja poznata je po formuli:

F = m * g.

U našem slučaju, faktor g je upravo centripetalno ubrzanje, koje je izvedeno iz prethodne formule. Samo u tom slučaju ulogu kamena će izvršiti nebesko tijelo, privučeno Zemljom, i uloga užeta - sila gravitacije. Množitelj g će se izraziti kroz radijus našeg planeta i brzinu njegove rotacije.

rezultati

Suština centripetalnog ubrzanja sastoji se u teškom i nezahvalnom poslu održavanja pokretnog tijela u orbiti. Postoji paradoksalan slučaj kada, uz konstantno ubrzanje, tijelo ne mijenja veličinu svoje brzine. Za netreniranog uma takva je izjava prilično paradoksalna. Ipak, pri izračunavanju gibanja elektrona oko jezgre i pri izračunavanju brzine rotacije zvijezde oko crne rupe centripetalno ubrzanje ne igra posljednju ulogu.