Krug i njegova svojstva. Okolna duljina

Okolnost u matematici jedna je od najvažnijih i najvažnijih figura. To je potrebno za različite izračune. Poznavanje svojstava ove figure iz školskog programa zasigurno će biti korisno u životu. Obujam je potreban za izračunavanje velikog broja materijala s okruglim presjekom. Napravite crteže, izgradite ogradu u blizini cvjetnjaka - to će zahtijevati znanje geometrijski oblik i njegova svojstva.

Koncept kruga i njegovi glavni elementi

Slika na ravnini koja se sastoji od brojnih točaka smještenih na jednakoj udaljenosti od središnje, naziva se krug. Segment koji izlazi iz središta i povezuje ga s jednom od točaka koje tvore krug naziva se radijus. Akord je segment koji međusobno povezuje par točaka smještenih duž perimetra kruga. Ako je postavljen tako da prolazi kroz središnju točku, onda je to i promjer.

Duljina radijusa kruga jednaka je duljini promjera, prepolovljena. Par neusklađenih točaka koje se nalaze na krugu, dijele ga na dva luka. Ako segment s krajevima u tim točkama prolazi kroz središnju točku (dakle promjer), tada će oblikovani lukovi biti polukružnici.

obujam

Izračun perimetra kruga određuje se na nekoliko načina: kroz promjer ili kroz radijus. U praksi je utvrđeno da duljina kruga (l) kada je podijeljena njegovim promjerom (d) uvijek daje jedan broj. Ovaj broj π, koji je jednak 3.141692666 ... Izračun se vrši po formuli: π = l / d. Transformiranjem se dobiva duljina kruga. Formula je sljedeća: l = πd.

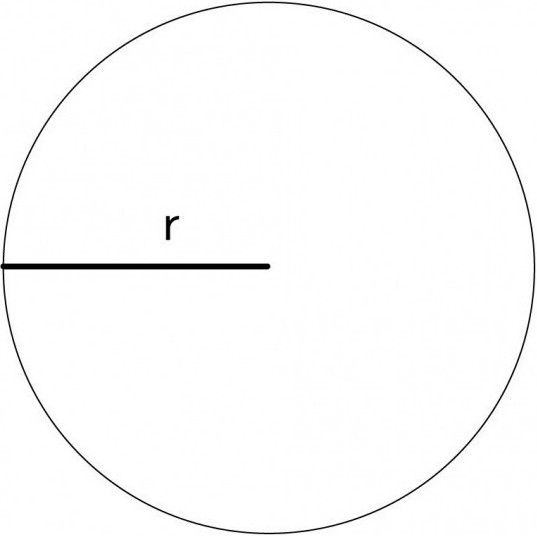
Da biste pronašli polumjer, primijenite sljedeću formulu: d = 2r. To je omogućeno podjelom. Naposljetku, radijus je pola promjera. Nakon što smo dobili gore navedene vrijednosti, možemo izračunati duljinu kruga koristeći sljedeću formulu: l = 2πr.

Osnovna svojstva

Područje kruga je uvijek veće u usporedbi s područjima drugih zatvorenih krivulja. Tangenta je linija koja dodiruje krug na samo jednoj točki. Ako ga linija presijeca na dva mjesta, onda je ona sekantna. Točka u kojoj su dva različita kruga u međusobnom dodiru uvijek je na ravnoj liniji koja prolazi kroz njihove središnje točke. Presijecanjem na ravnini nalaze se takvi krugovi koji imaju 2 zajedničke točke. Kut između njih izračunava se kao kut koji tangente formiraju na dodirne točke.

Ako kroz točku koja nije točka kruga, nacrtamo dvije ravne crte koje se razdvajaju na nju, tada će kut koji oni oblikuju biti jednak razlici u duljinama luka, prepolovljen. Ovo pravilo vrijedi iu suprotnom slučaju kada se radi o dva akorda. Dva ukrštena akorda tvore kut jednak zbroju duljina lukova, prepolovljenih. U ovome kutu biraju se lukovi u takvoj situaciji i na suprotnoj strani. Optičko svojstvo kruga glasi kako slijedi: zrake svjetlosti koje se reflektiraju od zrcala smještenih oko oboda kruga vraćaju se u njegovo središte. U tom slučaju, izvor svjetla mora biti instaliran na središnjoj točki kruga.