Cilindar. Pogledi, volumen cilindra, površina

Ime znanosti "geometrija" prevedeno je kao "mjerenje Zemlje". Nastao je nastojanjem prvih drevnih geodeta. I to je bilo ovako: tijekom poplava svetog Nila, vodeni tokovi ponekad su isprali granice poljoprivrednih područja, a nove granice nisu se mogle poklapati sa starim. Porezi seljaka isplaćivani su u faraonsku riznicu razmjerno količini zemljišta. Mjerenje površine obradivih površina u novim granicama nakon izlijevanja uključivalo je posebne ljude. Kao rezultat njihove aktivnosti pojavila se nova znanost, koja se razvila u staroj Grčkoj. Tamo je dobila ime i stekla gotovo moderan izgled. Kasnije je taj pojam postao međunarodni naziv znanosti o ravnim i trodimenzionalnim likovima.

Planimetrija je dio geometrije koja proučava ravne figure. Drugi dio znanosti je stereometrija, koja razmatra svojstva prostornih (trodimenzionalnih) figura. Ove brojke uključuju cilindar opisan u ovom članku.

Primjeri prisutnosti cilindričnih objekata u svakodnevnom životu obiluju. Gotovo svi detalji rotacije - osovine, čahure, vratovi, sjekire itd. - imaju cilindrični (znatno manje - konusni) oblik. Cilindar se široko koristi u graditeljstvu: tornjevi, potporni, ukrasni stupovi. I osim jela, neke vrste ambalaže cijevi različitih promjera. I na kraju - poznate kape, koje su dugo vremena postale simbolom muške elegancije. Popis je beskrajan.

Definicija cilindra kao geometrijske figure

Cilindar (kružni cilindar) naziva se lik koji se sastoji od dva kruga, koji se, po želji, kombiniraju uz pomoć paralelnog prijenosa. Ovi krugovi su baze cilindra. Ali linije (prave linije) koje povezuju odgovarajuće točke nazivaju se "generatori".

Važno je da su baze cilindra uvijek jednake (ako taj uvjet nije zadovoljen, onda je pred nama odsječen stožac, nešto drugo, ali ne cilindar) i nalaze se u paralelnim ravninama. Segmenti koji povezuju odgovarajuće točke na krugovima su paralelni i jednaki.

Kombinacija beskonačnog skupa generatora nije ništa drugo nego lateralna površina cilindra - jedan od elemenata toga geometrijski oblik. Druga važna komponenta su krugovi o kojima smo raspravljali gore. Zovu se baze.

Vrste cilindara

Najjednostavniji i najčešći tip cilindra je kružni. Formira se dvjema redovitim krugovima koji djeluju kao baze. Ali umjesto toga mogu postojati i druge brojke.

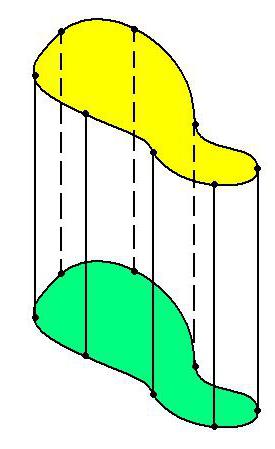
Osnove cilindara mogu oblikovati (osim krugova) elipse, druge zatvorene figure. Ali cilindar ne mora nužno imati zatvoreni oblik. Na primjer, parabola, hiperbola, druga otvorena funkcija može poslužiti kao baza cilindra. Takav cilindar će biti otvoren ili raspoređen.

Kut nagiba koji tvori osnove cilindara može biti ravan ili nagnut. Ravni cilindar koji je strogo okomit na ravninu baze. Ako se taj kut razlikuje od 90 °, cilindar je kosi.

Što je površina rotacije

Pravi kružni cilindar, bez sumnje - najčešća površina rotacije koja se koristi u inženjerstvu. Ponekad se iz tehničkih razloga koriste konusne, sferne, neke druge vrste površina, ali 99% svih rotirajućih osovina, osovina itd. izrađene točno u obliku cilindara. Da bismo bolje razumjeli što je površina revolucije, možemo razmotriti kako se sam cilindar oblikuje.

Pretpostavimo da postoji neka ravna crta a koja se nalazi vertikalno. ABCD je pravokutnik čija je jedna strana (segment AB) na liniji a . Ako zakrenete pravokutnik oko ravne linije, kao što je prikazano na slici, volumen koji zauzima, rotirajući će biti naše rotirajuće tijelo - ravni kružni cilindar visine H = AB = DC i radijus R = AD = BC.

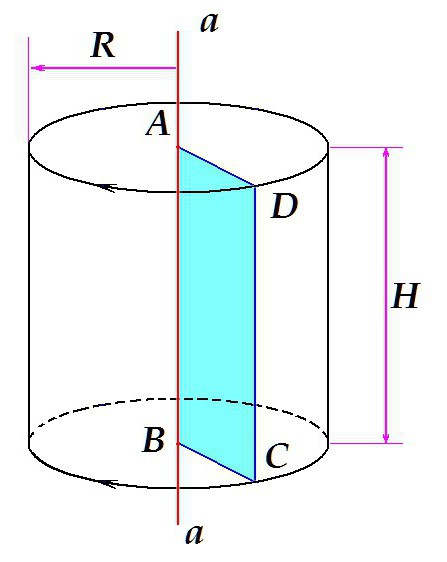
U ovom slučaju, kao rezultat rotacije figure - dobiva se pravokutnik - cilindar. Rotirajući trokut, možete dobiti konus, rotirajući polukrug - loptu, itd.

Površina cilindra

Da bi se izračunala površina pravilnog pravocrtnog kružnog cilindra, potrebno je izračunati površinu podloga i bočnu površinu.

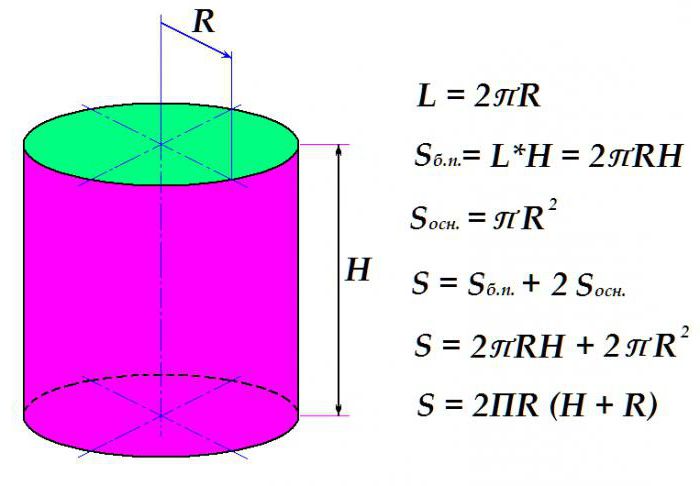
Prvo razmotrite kako izračunati površinu bočne površine. To je proizvod opsega cilindra po visini cilindra. Obod, zauzvrat je jednak dvostrukom proizvodu univerzalnog broja P i radijusa kruga.

Područje kruga, kao što je poznato, jednako je proizvodu P po kvadratu radijusa. Dakle, dodavanjem formula za područje određivanja bočne površine s dvostrukom ekspresijom osnovnog područja (postoje dvije od njih) i izradom jednostavnih algebarskih transformacija dobivamo konačni izraz za određivanje površine cilindra.

Određivanje veličine slike

Volumen cilindra određen je standardnom shemom: površina baze se množi s visinom.

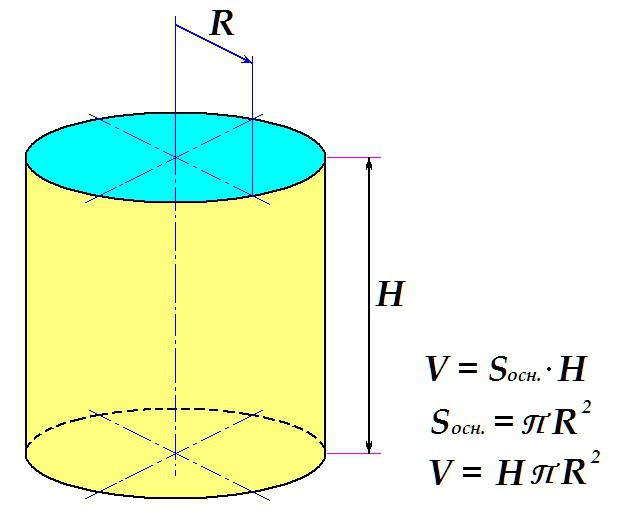
Dakle, konačna formula je sljedeća: željeni se definira kao produkt tjelesne visine univerzalnim brojem P i kvadratom radijusa baze.

Rezultirajuća formula, moram reći, primjenjiva je za rješavanje najneočekivanijih problema. Na isti način kao i volumen cilindra, na primjer, određuje se volumen električne instalacije. To je potrebno za izračun mase žica.

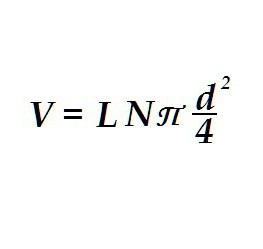
Razlika u formuli je samo u tome što umjesto radijusa jednog cilindra postoji promjer vodiča podijeljen na dva dijela, a broj živih u žici N pojavljuje se u izrazu. Također se umjesto visine koristi duljina žice. Tako se volumen "cilindra" ne izračunava od jednog, već od broja žica u pletenici.

Takvi su izračuni često potrebni u praksi. Doista, značajan dio spremnika za vodu izrađen je u obliku cijevi. A za izračunavanje volumena cilindra često je potrebno čak iu kućanstvu.

Međutim, kako je već spomenuto, oblik cilindra može biti različit. U nekim slučajevima potrebno je izračunati koliko je volumen nakošenog cilindra jednak.

Razlika je u tome što se površina podloge množi ne duljinom generatora, kao u slučaju ravnog cilindra, nego razmakom između ravnina - okomitog segmenta između njih.

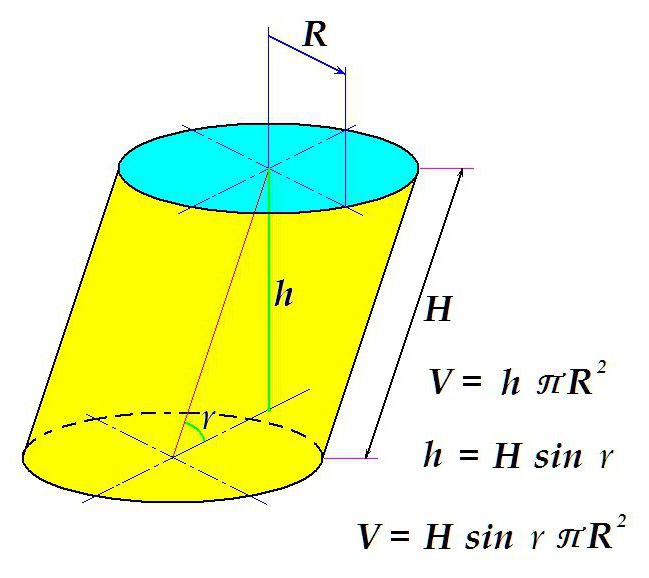
Kao što se može vidjeti iz slike, takav segment jednak je proizvodu duljine generatora i sinusa kuta nagiba generatora prema ravnini.

Kako izgraditi cilindrični zamah

U nekim slučajevima potrebno je izvući razvrtač cilindra. Na sljedećoj slici prikazana su pravila po kojima se napravi slijepa proba za izradu cilindra s danom visinom i promjerom.

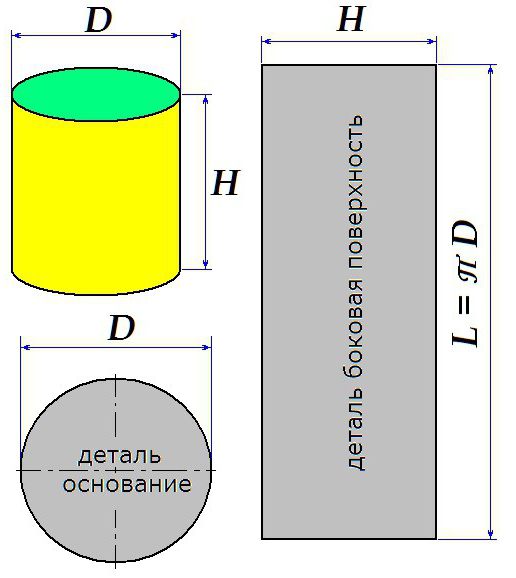
Imajte na umu da je slika prikazana bez obzira na šavove.

Razlike u konusu cilindra

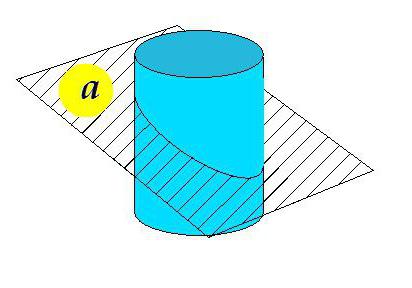
Zamislite određeni ravni cilindar omeđen s jedne strane ravninom okomitom na generatore. Ali ravnina koja cilja cilindar s druge strane nije okomita na generatore i nije paralelna s prvom ravninom.

Slika prikazuje nagibni cilindar. Ravnina i pod određenim kutom, različitima od 90 ° prema generatorima, prelaze sliku.

Takav geometrijski oblik češći je u praksi u obliku spojeva cijevi (koljena). No, postoje čak i zgrade izgrađene u obliku kosog cilindra.

Geometrijske karakteristike kosog cilindra

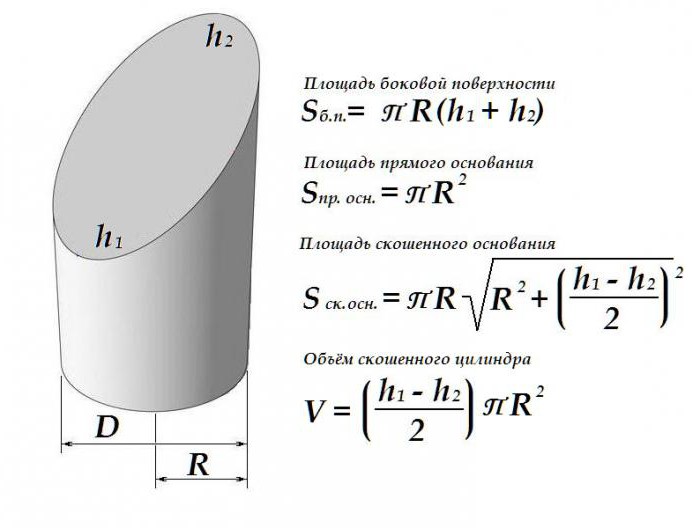
Nagib jedne od ravnina nagnutog cilindra neznatno mijenja redoslijed izračunavanja i površine takve figure i njenog volumena.