Stanje ravnoteže poluge. Pravilo trenutaka. Jednostavni mehanizmi. Zadaci i rješenja

Od pamtivijeka, čovječanstvo je koristilo različite mehanizme koji su dizajnirani da olakšaju fizički rad. Jedan od njih je poluga. Što je to, kakva je ideja njezine uporabe, a kakvo je stanje ravnoteže poluge, ovaj članak posvećen je razmatranju svih tih pitanja.

Kada je čovječanstvo počelo primjenjivati ​​načelo poluge?

Teško je točno odgovoriti na to pitanje, jer su drevni Egipćani i stanovnici Mezopotamije već poznavali jednostavne mehanizme još tri tisuće godina prije Krista.

Jedan od tih mehanizama je tzv. Poluga-dizalica. Predstavljao je dugačak stup, koji se nalazio na osloncu. Potonji je bio postavljen bliže jednom kraju pola. Pred krajem, koji je bio dalje od referentne točke, vezali su posudu, as druge su stavili neki protuuteg, na primjer, kamen. Sustav je podešen na takav način da je plovilo napunjeno na pola vodilo do vodoravnog položaja pola.

Dizalica je poslužila za podizanje vode iz bunara, rijeke ili druge depresije na razinu na kojoj je osoba bila. Primjenom male sile na posudu, osoba ju je spustila na izvor vode, posuda je bila napunjena tekućinom, a zatim je, primjenjujući malu silu na drugi kraj stupa s protuutegom, bilo moguće podići naznačenu posudu.

Legenda o Arhimedu i brod

Svatko poznaje starogrčkog filozofa iz grada Sirakuze, Arhimeda, koji je u svojim spisima ne samo opisao princip djelovanja jednostavnih mehanizama (poluga, nagnuta ploča), već je također rezultirao odgovarajućim matematičkim formulama. Do danas njegov izraz ostaje poznat:

Dajte mi uporište i ja ću pomaknuti ovaj svijet!

Kao što znate, nitko mu nije pružio takvu podršku, a Zemlja je ostala na svom mjestu. Međutim, ono što je Arhimed mogao stvarno pomaknuti bio je brod. Jedna od legendi Plutarha (djelo "Paralelni život") kaže sljedeće: Arhimed, u pismu svome prijatelju, kralju Hieronu iz Sirakuze, rekao je da bi sam mogao pomicati proizvoljno veliku težinu, pod određenim uvjetima. Hieron se iznenadio takvom izjavom filozofa i zamolio ga da pokaže o čemu govori. Arhimed je pristao. Jednog dana, brod Hieron, u doku, bio je natovaren ljudima i bačvama ispunjenim vodom. Filozof, koji je sjedio na udaljenosti od broda, uspio ga je podići iznad vode, povući uže, uz malo truda.

Dijelovi poluge

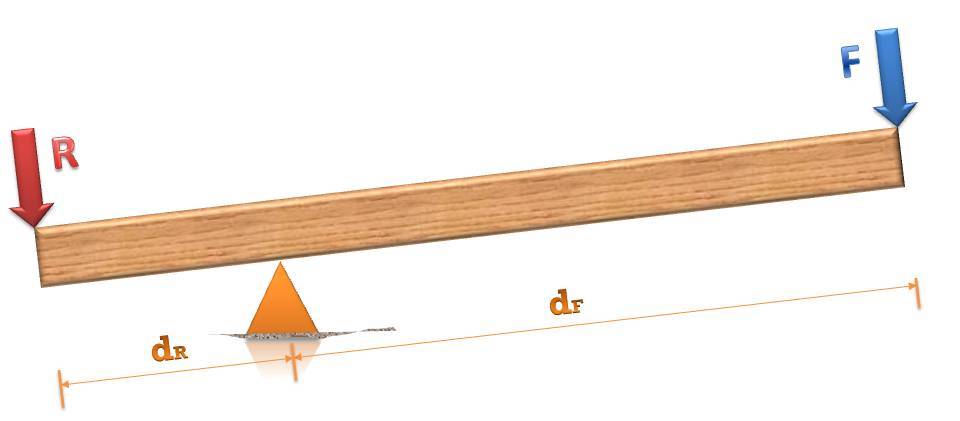
Unatoč činjenici da govorimo o prilično jednostavnom mehanizmu, još uvijek ima određeni uređaj. Fizički, sastoji se od dva glavna dijela: stupa ili grede i nosača. Pri razmatranju istih zadataka stup se smatra objektom koji se sastoji od dvije (ili jedne) ruke. Ramena je dio pola, koji je u odnosu na oslonac na jednoj strani. Veliku ulogu u principu djelovanja mehanizma koji se razmatra upravo je dužina ramena.

Kada razmatramo polugu u radu, onda postoje dva dodatna elementa: primijenjena sila i snaga za suprotstavljanje. Prvi nastoji pokrenuti predmet koji stvara silu reakcije.

Ravnotežno stanje poluge u fizici

Upoznajući se s uređajem ovog mehanizma, predstavljamo matematičku formulu, pomoću koje možemo reći koja će se ruka poluge pomicati u kojem smjeru ili, obratno, cijeli uređaj biti u stanju mirovanja. Formula ima oblik:

F ₁ x l ₁ = F ₂ x 1 ₂ ,

gdje su F1 i F2 sile djelovanja, odnosno reakcije, l ₁ i l ₂ su duljine krakova na koje se te sile primjenjuju.

Ovaj izraz vam omogućuje da istražite uvjete ravnoteže poluge koja ima os rotacije. Dakle, ako je rame l ₁ veće od l2, tada je za uravnoteženje sile F ₂ potrebna manja vrijednost F ₁ . Naprotiv, ako je l ₂ > l ₁ , tada za suprotstavljanje sili F2 _trebat ćete pričvrstiti veliki F1. Ovi zaključci mogu se dobiti ponovnim ispisivanjem gore navedenog izraza u sljedećem obliku:

F ₁ / F ₂ = l ₂ / l ₁ .

Kao što se može vidjeti, sile uključene u proces oblikovanja ravnoteže su inverzno povezane s duljinom krakova poluge.

Što je dobitak i gubitak kada koristite polugu?

Važan zaključak slijedi iz gornjih formula: uz pomoć duge ruke i malog napora mogu se pomicati predmeti s ogromnom masom. To je istina, a mnogi misle da upotreba poluge dovodi do dobitka u radu. Ali nije. Rad je količina energije koja se ne može stvoriti iz ničega.

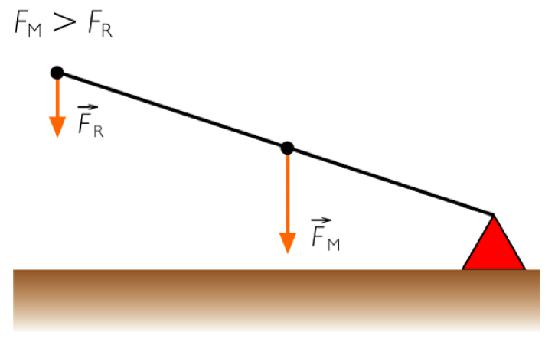
Analizirajmo rad jednostavne poluge koja ima dva stvrdnjavanja l1 i l2. Pretpostavimo da na kraju ramena l2 postoji težina P (F2 = P). Na kraju drugog ramena, osoba primjenjuje silu F ₁ i podiže to opterećenje na visinu h. Sada, izračunajmo rad svake sile i izjednačimo dobivene rezultate. Dobivamo:

F1xx = F2 * h.

Sila F ₂ djelovala je duž vertikalne putanje duljine h, a F _{1 je} djelovala i uzduž vertikale, ali je već bila pričvršćena za drugu ruku, čiji se kraj pomiče nepoznatom veličinom x. Da bi ga pronašli, potrebno je u zadnjem izrazu zamijeniti formulu veze između sila i ruku poluge. Izražavajući x, imamo:

x = F2 * h / F ₁ = l ₁ * h / l ₂ .

Ta jednakost pokazuje da li l ₁ > l ₂ , zatim F ₂ > F ₁ i x> h, tj. Primjenom male sile, možete podići teret s velikom težinom, ali morate pomaknuti odgovarajuću polugu (l ₁ ) na veću. udaljenost. Naprotiv, ako je l ₁ <l ₂ , tada F ₂ <F ₁ i x <h, to jest, težina određene težine može se podići na veću visinu h pomicanjem ramena l ₁ na manju amplitudu, ali morate primijeniti dovoljno veliku silu F ₁ , U prvom slučaju dobiva se pojačanje snage, u drugom na način ili brzinom.

Dakle, poluga ne profitira u radu, već dopušta samo redistribuciju u korist manje primijenjene sile ili u korist veće amplitude kretanja objekta. Opći filozofski princip djeluje u predmetu fizike o kojoj se raspravlja: svaki se dobit kompenzira određenim gubitkom.

Vrste poluga

Ovisno o točkama primjene sile i položaju nosača, razlikuju se sljedeće vrste ovog mehanizma:

• Prva vrsta: uporište je između dvije sile F ₁ i F ₂ , dakle duljina ruku će odrediti što daje takvu prednost. Primjer su obične škare.
• Druga vrsta. Ovdje se sila protiv koje se obavlja posao nalazi između potpore i primijenjene sile. Ova vrsta konstrukcije znači da će uvijek dati dobitak snage i gubitak putovanja i brzine. Njegov primjer je vrtni automobil.
• Treća vrsta. Posljednja opcija, koja ostaje da se ostvari u ovom jednostavnom dizajnu, je položaj primijenjene sile između oslonca i sile otpora. U ovom slučaju, dobitak na putu, ali gubitak je na snazi. Primjer bi bio pinceta.

Pojam trenutka sile

Razmatranje bilo kakvih problema u mehanici, koji uključuju koncepte osi ili točke zakretanja, provodi se pomoću pravila o momentu sile. Budući da je potpora poluge također i os (točka) oko koje se sustav okreće, trenutak sile se također koristi za procjenu ravnoteže tog mehanizma. Pod time se podrazumijeva količina u fizici, jednaka proizvodu ramena i djelovanja sile, to jest:

M = l * F.

S obzirom na tu definiciju, stanje ravnoteže poluge može se prepisati na sljedeći način:

M1 = M2, gdje M1 = l1 * F1 i M2 = l2 * F2.

Trenutak M je aditivan, što znači da se ukupni moment sile za dotični sustav može dobiti uobičajenim dodavanjem svih trenutaka M _{i koji} djeluju na njega. Međutim, treba uzeti u obzir njihov znak (sila koja uzrokuje da se sustav okrene u smjeru suprotnom od kazaljke na satu stvara pozitivan trenutak + M, i obrnuto). S tim u vezi, pravilo trenutaka za ravninu koja je u ravnoteži će izgledati ovako:

M1-M2 = 0.

Poluga gubi ravnotežu kada M ₁ ≠ M ₂ .

Gdje se koristi načelo poluge?

Već smo naveli neke primjere korištenja ovog jednostavnog i dobro poznatog mehanizma iz antičkih vremena. Evo samo nekoliko dodatnih primjera:

• Kliješta: poluga prve vrste, koja vam omogućuje stvaranje ogromnih napora zbog male duljine ramena l ₂ gdje se nalaze zubi alata.
• Otvori za poklopce limenki i boce: to je poluga druge vrste, tako da uvijek daje dobitak u naporu.
• Šipka za ribolov: poluga 3. vrste, koja vam omogućuje da pomičete kraj štapa za ribolov s plutačom, sječom i kukom za velike amplitude. Gubitak u ovom slučaju osjeća se kada ribar teško može izvući ribu iz vode, čak i ako njezina težina ne prelazi 0,5 kg.

Čovjek sam svojim zglobovima, mišićima, kostima i tetivama živ je primjer sustava s mnogo različitih poluga.

Rješavanje problema

Ravnotežno stanje poluge o kojem se raspravlja u članku koristi se za rješavanje jednostavnog problema. Potrebno je izračunati približnu duljinu poluge, primjenjujući napor do kraja kojeg je Arhimed mogao podići brod, kao što Plutarh opisuje.

Da bismo to riješili, uvodimo sljedeće pretpostavke: uzimamo u obzir grčku triremu od 90 tona s pomakom i pretpostavljamo da je potpora poluge bila 1 metar od središta mase. Kako je Archimedes, prema legendi, lako mogao podići brod, pretpostavit ćemo da je u tu svrhu primijenio silu jednaku polovici njegove težine, odnosno oko 400 N (za masu od 82 kg). Zatim, primjenjujući stanje ravnoteže poluge, dobivamo:

F ₁ * l ₁ = F ₂ * l ₂ => l ₁ = F ₂ * l ₂ / F ₁ = m * g * l ₂ / F ₁ = 90000 * 9,81 * 1/400 ≈ 2,2 km.

Čak i ako povećamo silu koja se primjenjuje na vrijednost težine samog Arhimeda i donosimo potporu još dva puta, tada će dužina ramena biti oko 500 metara, što je također velika vrijednost. Najvjerojatnije, legenda o Plutarhu je pretjerivanje da bi se pokazala učinkovitost poluge, a Arhimed nije zapravo podigao brod iznad vode.