Eksponiranje: Osnovna matematika u programiranju

Često smo suočeni s činjenicom da moramo povećati broj u bilo kojem stupnju. Možete koristiti uobičajeni kalkulator. Ali to nije zanimljivo i vrlo često ne odgovara uvjetima zadatka.

Pojam stupnja iz matematike

Trebalo bi započeti objašnjenjem matematičkog značenja eksponenta. Na primjer, moramo podići neki broj x na snagu y. U matematici, ovaj unos bi izgledao ovako: x ^y = x ^ y. To znači da se broj x mora množiti sam po sebi y puta. Zapamtite: bez obzira na broj koji gradite na nulti stupanj, dobivate ga, a kada izgradite prvu snagu, dobivamo naš izvorni broj. U konstrukciji negativnog stupnja samo okrećemo rezultat.

Eksponiranje u paskalu

Uz matematiku, sve je jasno. Ali kako napraviti takav program, koji će proizvesti eksponencijaciju? Jednostavno je. Ako trebamo podići x na snagu od 5, tada će naš kod izgledati ovako: res: = x * x * x * x * x. Broj x uvećali smo 5 puta, kao što nam je to bilo potrebno, ali što učiniti ako ne znamo u kojoj mjeri treba povećati broj? Zatim ćemo razmotriti kako napraviti eksponiranje. Pascal nam ne daje mnogo mogućnosti za to, ali definitivno ćemo smisliti nešto. Primjerice, korištenjem standardnih funkcija i postupaka ili korištenjem različitih ciklusa.

Kvadriranje broja

Počnimo s izgradnjom trga. Kvadratiranje je poseban slučaj eksponentiranja. Da biste to učinili, pascal osigurava standardni postupak sqr (x). To će povećati naš broj x na kvadratu, ovaj zapis je jednak zapisu x * x.

Vrlo često je to sasvim dovoljno, ali ne uvijek program može biti ograničen na samo jedno kvadriranje. Kako izgraditi viši stupanj? Čitajte o tome i educirajte.

Korištenje standardnih operatora

U Pascalu postoje dvije metode za podizanje broja na snagu: exp (ln (x) * y) i metoda (x, y). Postupak exp () ima ograničenje: x mora biti veći od 0, budući da nemoguće je izvaditi prirodni logaritam iz nepozitivnog broja, ali se ta funkcija smatra zastarjelom i neprikladnom za korištenje, stoga o tome više nećemo govoriti. Funkcija power () uzima dvije vrijednosti, a prvi broj (x) se povećava na snagu, drugi broj (y) na snagu koja se podiže i vraća x na snagu y. Treba imati na umu da su brojevi x i y stvarni, odnosno stvarni.

No, postoji jedan nedostatak, ova značajka nije u svim verzijama Pascala. U svakom slučaju, ponekad se eksponentiranje mora izvesti bez korištenja operatora. Nastavite i rastavite sljedeću metodu.

Eksponiranje s petljom for

Kao što smo već razumjeli, podizanje broja na moć je višestruko umnožavanje broja. Ponavljanje akcije više puta u programiranju mnogo je lakše nego u životu. Upotrijebite petlju for:

Mi ćemo razumjeti što i kako radi ovdje. Za početak uvodimo dva broja: x i y. Zatim uzimamo jedinicu za rezultat, za koji je - ispod. Izvedite ciklus do modula našeg stupnja, jer ako je stupanj negativan, ciklus neće ići. U petlji, svoj rezultat pomnožimo s brojem x. Pa zašto dodijeliti rezultat na 1? Prvo, ako pomnožimo s 0, program će uvijek dati 0. Drugo, naš stupanj može biti jednak 0, onda nam program treba vratiti 1, jer bilo koji broj u 0 stupnjeva je 1. Zatim provjeravamo je li stupanj negativan ili pozitivan: ako je negativan, podijelimo jedinicu našim rezultatom. Izvođenje ovog zadatka s petljom dok se obavlja na isti način.

Korištenje petlje u eksponentu

Korištenje petlje while je ispravnije nego za, ali je prethodna verzija lakša za razumijevanje. Teško je moguće ograničiti se samo na jedan za petlju, jer bi za razumijevanje bilo bolje pogledati nekoliko primjera, a zadatak je postavljen drugačije, za nekoga s jednim ciklusom, za nekoga drugoga, zato ćemo analizirati još jednu metodu eksponiranja.

Sve je gotovo isto kao i prije. Unesite dva broja x i y. Mi dodijelimo jediničnu vrijednost našem rezultatu kako bismo se podigli na nulti stupanj. Tada kreiramo brojač i dodajemo mu vrijednost modula našeg stupnja. Ciklus se nastavlja sve dok brojač ne postane nula, ako je stupanj nula od samog početka, ciklus se neće izvršiti, rezultat će ostati jedan, kao što bi trebao biti, jer je bilo koji broj u nultom stupnju jedan. U samom ciklusu još uvijek smatramo rezultat, umnožavajući već dobiveni rezultat našim brojem x, ne zaboravimo oduzeti jedan od našeg brojača, inače nikada nećemo doseći nulu. Pa onda, kao i gore, pretvorba ako je stupanj bio negativan. Ništa komplicirano, kako se ispostavilo. Međutim, nitko nije sumnjao.

Pa, završili smo s običnim brojevima, ali ne postoje samo takvi brojevi.

Koncept složenih brojeva

Od samog početka školovanja, objašnjavaju nam se samo obični brojevi, ali postoje i drugi, na primjer, složenih brojeva. Teško ih je zamisliti, pogotovo s obzirom na činjenicu da ih gotovo nikad nismo upoznali. U matematičkoj notaciji oni imaju oblik z = x + yi, gdje su x i y neki brojevi, i i je mentalna jedinica. Odmah ste pomislili: ovo je čest broj, samo trebate izvršiti operaciju dodavanja. Ali ne, nije tako jednostavno. To nije suma, to je broj. Drugim riječima, ako sve to pokušate prikazati sa stajališta geometrije, tada se znak dodavanja može zamijeniti točka-zarezom i dobiti koordinate točke, x i y. I ako izgradimo nulti vektor do ove točke, onda možemo vizualno vidjeti sve to. Čini se da je tekst postao previše, da vidimo malo:

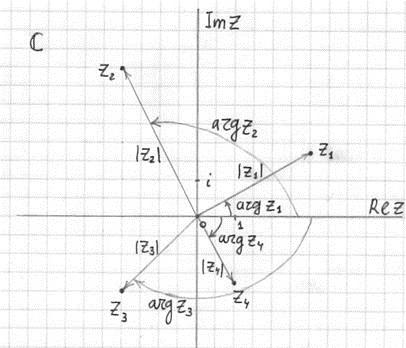
Ako želimo pokazati da je naš zrakoplov složen, dovoljno je označiti ga slovom C, ovako. Tada možemo vidjeti puno točaka, pogledajmo ih i pokušati shvatiti koji je od njih zabilježen. Uzmimo točku z _1, spustimo projekciju na osi ReZ i dobijemo 3, zatim na osi lmZ i dobijemo 1.75, što rezultira brojem z ₁ = 3 + 1.75i. Čini se da je sve jasno, još jednom, da se konsolidiramo. Točka z ₂ , na horizontalnoj osi - dvije, na okomitoj - četiri, kao rezultat toga imamo: z ₂ = 2 + 4i. Sve je vrlo jasno i jednostavno.

Kod složenih brojeva moguće su sve iste operacije kao i kod običnih. Zbrajanje, oduzimanje, množenje, dijeljenje. No, u ovom članku ćemo se usredotočiti na izgradnju kompleksnog broja moći.

Podizanje snage kompleksnog broja

Što učiniti ako trebate izgraditi kompleksan broj? Nemojte paničariti! Sve je potpuno isto kao kod običnih brojeva, ali malo složenije. Počnimo s kvadratom. S obzirom na broj z = 2 + 5i. Kvadrat, dobimo z ² = (2 + 5i) ² = (2 + 5i) (2 + 5i) - a ovo je uobičajeno dvočlano, možete jednostavno pomnožiti, dati slične pojmove i sve. To je vrlo jednostavno, ali što učiniti kada trebate graditi na viši stupanj? Za početak, naš broj treba biti prikazan u trigonometrijskom obliku, na primjer:

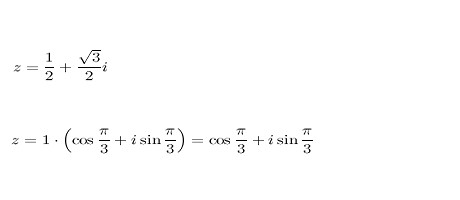
Tada je potrebno koristiti formulu za konstruiranje kompleksnih brojeva u trigonometrijskom obliku: z ⁿ = | z | ⁿ * (cos (nx) + i * sin (nx)). Može se primijetiti da u izgradnji složenih brojeva, čak iu vrlo velikoj mjeri, oni se ne mijenjaju mnogo, pa ne brinite, to je teško, ali s praksom će sve doći.

Dakle, sada znate kako podići brojeve na moć u matematici, u programskom jeziku Pascal, također ste naučili što su kompleksni brojevi i kako ih izgraditi na moć. Sve je ispalo mnogo jednostavnije nego što ste mislili. Nije li? Ostaje samo pokušati sve na vlastitom iskustvu, i sve će pasti na svoje mjesto. Svaki zadatak koji se odnosi na eksponiranje sada je vrlo lako riješen za vas.