Viskoznost fluida Metode za određivanje viskoznosti tekućine

U industriji, istraživačke aktivnosti često moraju izračunati viskoznost tekućine. Rad s običnim ili raspršenim medijem u obliku aerosola, plinske emulzije zahtijeva poznavanje fizikalnih svojstava tih tvari.

Što je viskoznost tekućine?

Čak je i Newton postavio takvu znanost kao reologiju. Ova industrija se bavi proučavanjem otpora tvari u pokretu, tj. Viskoznosti.

U tekućinama i plinovima dolazi do kontinuirane interakcije molekula. Udaraju se, odbijaju ili jednostavno prolaze. Kao rezultat, slojevi materije međusobno djeluju, dajući brzinu svakom od njih. Fenomen takve interakcije molekula tekućina / plinova naziva se viskoznost, odnosno unutarnje trenje.

Da bi se taj proces bolje razmotrio, potrebno je pokazati iskustvo s dvije ploče između kojih se nalazi tekući medij. Ako pomaknete gornju ploču, tada će se sloj tekućine "zaglaviti" na njega također pomicati s određenom brzinom v1. Nakon kratkog vremenskog perioda, primijetimo da se slojevi ispod tekućine također kreću duž iste putanje pri brzini od v2, v3 ... vn, itd., S v1> v2, v3 ... vn. Stopa najnižeg od njih ostaje nula.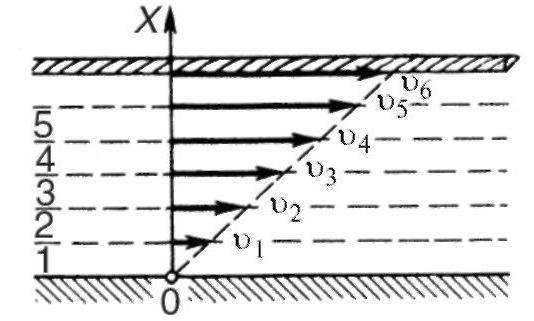

Primjenom plina, kao primjer, gotovo je nemoguće provesti takav eksperiment, budući da su sile međusobne interakcije molekula vrlo male i vizualno se ne mogu registrirati. Ovdje se također govori o slojevima, o brzini kretanja ovih slojeva, dakle u plinovitim medijima postoji i viskoznost.

Newtonovi i ne-Newtonski mediji

Newtonska tekućina je tekućina čija se viskoznost može izračunati pomoću Newtonove formule.

Takva okruženja uključuju vodu i otopine. Viskoznost tekućine u takvim okruženjima može ovisiti o faktorima kao što su temperatura, tlak ili atomska struktura tvari, ali gradijent brzine će uvijek ostati isti.

Ne-Newtonske tekućine su mediji u kojima se gore navedena vrijednost može promijeniti, što znači da Newtonova formula ovdje neće djelovati. Takve tvari uključuju sve dispergirane medije (emulzije, aerosole, suspenzije). To uključuje i krv. O tome ćemo detaljnije raspravljati u nastavku.

Krv kao unutarnje tijelo tijela

Kao što znate, 80% krvi je plazma, koja ima tekuće agregatno stanje, a preostalih 20% su crvene krvne stanice, trombociti, bijele krvne stanice i razne inkluzije. Humani eritrociti imaju promjer od 8 nm. U stacionarnom stanju oni tvore agregate u obliku novčića, dok značajno povećavaju viskoznost tekućine. Ako je protok krvi aktivan, te se “konstrukcije” raspadaju, a unutarnje trenje se smanjuje.

Omjeri srednje viskoznosti

Međusobno djelovanje slojeva medija međusobno utječe na karakteristike cijelog sustava tekućine ili plina. Viskoznost je jedan primjer fizičke pojave kao što je trenje. Zahvaljujući tome, gornji i donji slojevi medija postupno izjednačavaju brzine svoje struje i na kraju je jednaka nuli. Viskoznost se također može okarakterizirati kao otpornost jednog sloja medija na drugi.

Za opisivanje takvih pojava postoje dvije kvalitativne karakteristike unutarnjeg trenja:

• dinamički koeficijent viskoznosti (dinamička viskoznost tekućine);
• kinetički koeficijent viskoznosti (kinetička viskoznost).

Obje veličine povezane su jednadžbom υ = η / ρ, gdje je ρ gustoća medija, υ kinetička viskoznost, a η dinamička viskoznost.

Metode određivanja viskoznost tekućine

Viskozimetrija je mjerenje viskoznosti. Na sadašnjem stupnju razvoja znanosti moguće je na praktičan način pronaći vrijednost viskoznosti tekućine na četiri načina:

1. Metoda kapilara. U tu svrhu potrebno je imati dvije posude povezane staklenim kanalom malog promjera poznate duljine. Također morate znati vrijednosti tlaka u jednoj posudi iu drugoj. Tekućina se stavlja u stakleni kanal i tijekom određenog vremena teče iz jedne tikvice u drugu.

Daljnji proračuni izvode se pomoću Poiseuilleove formule za pronalaženje vrijednosti koeficijenta viskoznosti tekućine.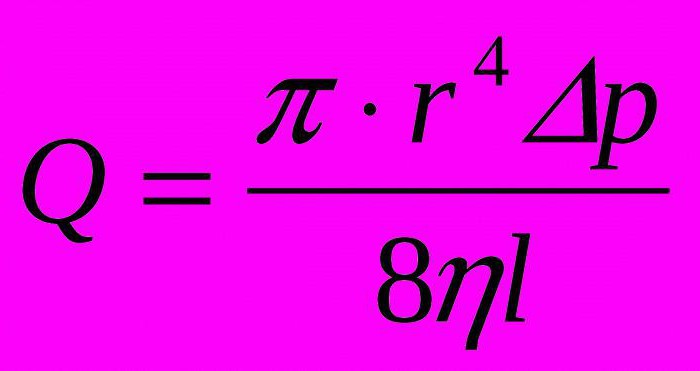

U praksi, tekući mediji mogu biti smjese zagrijane na 200-300 stupnjeva. Obična staklena cijev u takvim bi se uvjetima jednostavno deformirala ili čak rasprsnula, što je neprihvatljivo. Moderni kapilarni viskozimetri sastavljeni su od visokokvalitetnog i otpornog materijala koji lako podnosi takva opterećenja.

2. Medicinska metoda prema Hessenu. Za izračun viskoznosti tekućine na ovaj način potrebno je imati ne jednu, već dvije identične kapilarne instalacije. U jednom od njih stavite okolinu s prethodno poznatom vrijednošću unutarnjeg trenja, au drugom - ispitnom tekućinom. Zatim izmjerite dvije vremenske vrijednosti i sastavite omjer kojim dosežu željeni broj.

3. Rotaciona metoda. Za njegovu provedbu potrebno je imati konstrukciju od dva koaksijalna cilindra. To znači da jedan od njih mora biti unutar drugog. U razmaku između njih sipati tekućinu, a zatim dati brzinu unutarnjem cilindru. ovo kutna brzina Tekućina je također prijavljena. Razlika u snazi ​​trenutka omogućuje nam izračunavanje viskoznosti medija.

4. Određivanje viskoznosti tekućine metodom Stokes. Da bi se to iskustvo ostvarilo, potrebno je imati Goppler viskozimetar, koji je cilindar napunjen tekućinom. Prije početka pokusa stavite dvije oznake na cilindar i izmjerite duljinu između njih. Zatim uzmite kuglicu određenog radijusa R i spustite je u tekući medij. Da biste odredili brzinu pada, pronađite vrijeme kretanja objekta iz jedne etikete u drugu. Znajući brzinu lopte, moguće je izračunati viskoznost tekućine.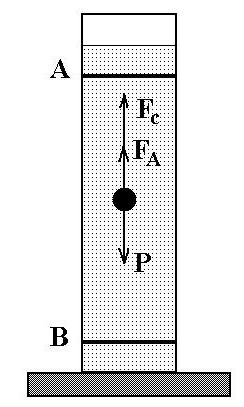

Praktična uporaba viskozimetara

Određivanje viskoznosti tekućine je od velike praktične važnosti u industriji rafiniranja nafte. Prilikom rada s višefaznim disperznim medijima, važno je poznavati njihova fizička svojstva, osobito unutarnje trenje. Moderni viskozimetri izrađeni su od izdržljivih materijala, au njihovoj proizvodnji koriste naprednu tehnologiju. Sve to zajedno omogućuje rad s visokom temperaturom i tlakom bez štete za samu opremu.

Viskoznost fluida igra veliku ulogu u industriji jer transport, obrada i proizvodnja, na primjer, ulja ovisi o vrijednostima unutarnjeg trenja tekuće smjese.

Koja je uloga viskoznosti u medicinskoj opremi?

Protok mješavine plina kroz endotrahealnu cijev ovisi o unutarnjem trenju tog plina. Promjena viskoznosti medija ovdje ima različit učinak na prodiranje zraka kroz uređaj i ovisi o sastavu smjese plinova.

Uvođenje lijekova, cjepiva kroz štrcaljku također je živopisan primjer djelovanja viskoznosti medija. Govorimo o padu tlaka na kraju igle pri ubrizgavanju tekućine, iako se u početku vjerovalo da se taj fizički fenomen može zanemariti. Pojava visokog tlaka na vrhu rezultat je unutarnjeg trenja.

zaključak

Viskoznost medija je jedna od fizikalnih veličina, koja ima veliku praktičnu primjenu. U laboratoriju, industriji, medicini - u svim tim područjima često se pojavljuje koncept unutarnjeg trenja. Rad najjednostavnije laboratorijske opreme može ovisiti o stupnju viskoznosti medija koji se koristi za istraživanje. Čak i prerađivačka industrija ne može bez znanja u području fizike.