Fresnelova difrakcija na kružnoj rupi i disku

Difrakcija svjetlosti očituje se u svjetlosnom valu koji se savija oko malih prepreka, dok se odstupanja od zakona geometrijske optike promatraju. To vrijedi i za svjetlosne valove koji prolaze kroz rupu, na primjer, u objektivu kamere ili kroz zjenicu oka. Tu je Fresnelova i Fraunhoferova difrakcija. Razlike se sastoje u veličini udaljenosti između izvora svjetlosti, prepreke i zaslona na kojem se promatra slika te pojave.

Mjesto difrakcije u općem nizu optičkih pojava

Prolaz svjetla (i općenito elektromagnetski valovi kroz različite nehomogene medije popraćeno je pojavama njihove refleksije, difrakcije i refrakcije. Kada val dosegne granicu dvaju medija, podijeljen je na reflektirani, koji ostaje u izvornom mediju, ali s promjenom smjera propagacije i lomljenim, koji prolazi kroz granicu medija, ali i promjenom smjera. Fresnelova difrakcija je proces promjene smjera svjetlosnog vala kada se ne susreće s granicama dvaju medija, već s nekom neprozirnom preprekom s rupom (ili bez nje, ali malih dimenzija) u istom mediju. Stupanj difrakcije raste s povećanjem duljine svjetlosnog vala.

Fenomen otkrića

Vjerojatno prvi koji je primijetio difrakciju bio je Francesco Maria Grimaldi (2. travnja 1618. - 28. prosinca 1663.), talijanski jezuitski svećenik i istovremeno matematičar i fizičar koji je predavao na isusovačkom fakultetu u Bologni. Drugu polovicu svog života posvetio je proučavanju astronomije i optike.

Grimaldi je bio poznat po svom djelu pod nazivom "Fizička znanost o svjetlu, cvijeću i duge", koji je objavljen u Bologni 1665. godine. Većina se sastoji od dosadne rasprave o prirodi svjetla s teološkog stajališta i danas nije zanimljiva. Međutim, pored toga, knjiga sadrži prikaze brojnih eksperimenata vezanih uz difrakciju svjetlosnih zraka.

Na temelju svakodnevnog iskustva, ljudi su u davna vremena zaključili da se zrake svjetlosti šire u ravnim linijama. Naposljetku, objekt koji je između, na primjer, plamena svijeće i zida, baca sjenu s oštrom granicom, kao da se izravne zrake svjetlosti na nejasnoj barijeri lome.

Međutim, rezultati pokusa Grimaldija proturječili su tim idejama uspostavljenim tisućama godina. Ispada da ako osvijetlite različite objekte kroz prepreku s malom rupom, onda sjene od njih neće biti iste kao u odsutnosti prepreke. Pokazalo se da svjetlo može promijeniti smjer razmnožavanja i obići male prepreke.

Kako je otkrivena Fresnelova difrakcija na okruglom otvoru

Grimaldi, prenoseći svjetlost sunca u tamnu sobu kroz malu rupu (otvor), primijetio je da je širina sjene tankih predmeta poput igala i dlaka na ekranu mnogo veća (kao što se vidi na slici ispod) nego što bi bilo kad bi zrake svjetlosti prolazile ravne linije.

Također je primijetio da je krug svjetla koji se na ekranu formirao zrakama koje prolaze kroz vrlo malu rupu u olovnoj ploči bio očito veći nego što bi bio da su te zrake pale ravno na ekran. Grimaldi je zaključio da mijenjaju smjer kada prolaze blizu rubova rupe.

U svojim pokusima, provedenim u istoj prostoriji, svjetlo u koje je došlo kroz rupe u kapcima, udaljenost između prepreke za svjetlosne valove (ploča s okruglom rupom) i zaslon je bio mali. Fresnelova difrakcija također odgovara tim uvjetima. Analizirajući ga, ne možemo zanemariti zakrivljenost fronte kao početni val na prepreku i sekundarne valove. Oni daju zaslonu difrakcijsku sliku prepreke s rupom, kao što je prikazano na slici ispod.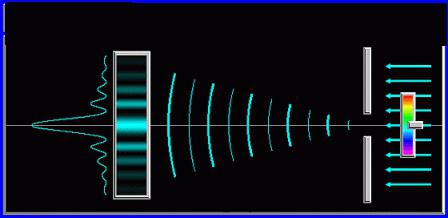

Što će se dogoditi ako svjetlo padne na malu neprozirnu prepreku

Grimaldi je također otkrio da je sjena malog tijela (nepravilnog oblika) bila okružena s tri obojene pruge ili vrpce, koje su se sužavale dok su se udaljavale od središta sjene. Ako je izvorni svjetlosni tijek bio jači, reproducirao je slične trake u području same sjene: postojale su dvije ili više takvih traka, a njihov se broj povećavao razmjerno udaljenosti između sjene i osvijetljenog tijela.

I u ovom slučaju, Grimaldi je uspio promatrati fenomen, koji je kasnije nazvan "Fresnelova difrakcija", zbog čega je na zaslonu dobivena difrakcijska slika prepreke. Analitički izračunati je vrlo teško. Međutim, postoje metode koje dopuštaju da se u određenim slučajevima znatno pojednostavi ovaj izračun.

I još jedna primjedba o Grimaldijevim eksperimentima. Ako bi koristio okrugli disk (na primjer tanjurić) kao zaslon u njima, onda bi možda mogao promatrati tako nešto kao što je Fresnelova difrakcija na okruglom disku stoljeće i pol ranije nego što se zapravo dogodilo. No povijest općenito i povijest znanosti posebno ne znaju. konjunktiv. Stoga je ovaj pokus proveden tek početkom 19. stoljeća. (vidi dolje).

Prvo promatranje smetnji

preskakanje sunčeve zrake u prostoriju kroz nekoliko malih okruglih rupa, Grimaldi je na ekranu dobio tragove preklapajućih konusa svjetlosti. Kao što se moglo i očekivati, na mjestima gdje su padale zrake iz dvije rupe, ekran je bio osvijetljen više nego što bi bio iz jednog konusa svjetla; ali istraživač se iznenadio kad je otkrio da su dijelovi cjelokupne sjene, u kojima su stožci svjetla nadsvođeni jedan na drugoga, bili tamniji od odgovarajućih dijelova, u kojima nije bilo prekrivača (slika ispod). 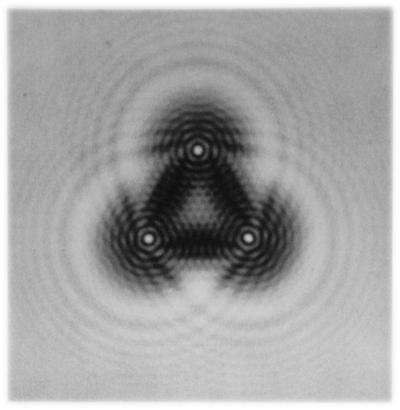Tako je po prvi put zabilježeno da osvijetljeno tijelo može postati tamnije ako dodamo svjetlo onome koje već prima. Sada znamo da je razlog tome interferencija, tj. Međusobno pojačavanje ili slabljenje svjetlosnih valova. Ona se također očituje u takvoj pojavi kao što je Fresnelova difrakcija. Mnogi suvremeni znanstvenici ni temeljno ne razlikuju te koncepte, reducirajući sve difraktivne manifestacije na manifestacije interferencije, kao što je to učinio, na primjer, R. Feynman u trećem svesku njegovog "Feynmanovog predavanja o fizici".

Od Grimaldija do Huygensa i Newtona

Prvi pokušaj objašnjenja razloga za odstupanje svjetla od pravocrtnog širenja učinio je poznati engleski znanstvenik R. Guk. On je sugerirao da je svjetlost val oscilacija svjetskog etera, koji je tada shvaćen kao sveprožimajuća tvar koja ispunjava sav prostor. Hookeova ideja već je postavila temelje za buduće ispravno objašnjenje o tome što su Fresnelova difrakcija i svi optički fenomeni. Međutim, on nije bio u stanju stvoriti odgovarajuću kvantitativnu teoriju.

Sljedeći korak je napravio Christian Huyges, koji je svoj poznati princip formulirao 1690. Prema njemu, vidljivo svjetlo je skup sfernih valova koji se šire od izvora u svim smjerovima u eteru. U ovom slučaju, izvor tih valova mogu biti ne samo eterske čestice pobuđene izravno iz izvora svjetlosti (na primjer, plamen svijeće), nego i bilo koje druge njegove čestice na mjestima u prostoru koje svjetlo prolazi tijekom propagacije. Dobiveni vidljivi val je u bilo kojem trenutku kao omotač svih sekundarnih valova. Potonje se može proširiti izvan granica prepreka na putu svjetlosti, što se dobro prekriva slikama njihovih sjena koje se promatraju tijekom difrakcije. Prema tome, prema toj teoriji, jednostavno nema prepreka oko svjetla - iz novih (sekundarnih) izvora koji se proteže izvan prepreka.

Međutim, prema Huygensovom načelu, uske svjetlosne zrake su uopće nemoguće - njihovi se rubovi trebaju odmah širiti u svim smjerovima. Međutim, oni se mogu vidjeti golim okom, kao što je to bilo u pokusima Grimaldija. Postojala je kontradikcija između teorije i prakse.

I. Newton pokušao ga je prevladati u svojoj korpuskularnoj teoriji svjetla, koja je također dala objašnjenja svim optičkim pojavama, uključujući i difrakciju Fresnelove svjetlosti. Međutim, glavni postulat Newtona da svjetlost nije val u zraku, već tok tijela (korpuskula), potaknuo je druge kontradikcije. Dakle, nije bilo jasno zašto sjecišta svjetlosti ne utječu jedni na druge, budući da bi se krvne stanice trebale sudariti jedna s drugom. No autoritet Newtona bio je toliko visok da je valna teorija svjetla bila zaboravljena više od stotinu godina.

Povratak svjetlosnih valova

Godine 1880. engleski fizičar T. Jung predložio je povratak na valnu teoriju svjetla, dopunjenu konceptom interferencije svjetlosnih valova. To znači da kada se koherentni (s jednakim frekvencijama) valovi međusobno preklapaju, vremenski intenzitet intenziteta svjetla u nekim točkama polja i prigušenje kod drugih ovisno o omjeru faza dodanih svjetlosnih valova je stabilan.

Pojam ometanja koristio je francuski fizičar O. Fresnel kako bi ih dopunio Huygensovim načelom. Prema njegovoj varijanti, svi sekundarni sferni valovi su koherentni i ometaju nametanje. Koji je fizički mehanizam Huygens-Fresnelove difrakcije?

Prolazak svjetla kroz okruglu rupu

Kada se svjetlosni val širi kroz rupu, odnos između njegovog promjera i valne duljine upadnog snopa određuje ponašanje svjetla. Kao što je prikazano na lijevoj strani slike ispod, kada je valna duljina znatno manja od promjera rupe, ona jednostavno prolazi naprijed u ravnoj liniji, kao da uopće nema prepreka.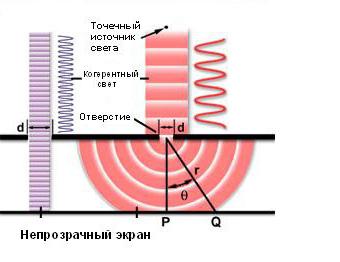

Međutim, na desnoj strani slike prikazana je drugačija situacija. U tom slučaju valna duljina svjetlosti koja se prenosi iz točkastog izvora prelazi promjer otvora, a na otvoru se javlja Fresnelova difrakcija. Kada se analizira ovaj fenomen, smatra se da je rupa odsutna, a umjesto nje postavljen je skup fiktivnih sekundarnih izvora svjetlosti koji pobuđuju iste sekundarne sferne valove, koji su već spomenuti. Oni se šire u smjeru ekrana i dosežu različite točke s različitim fazama, ometajući međusobno, tj. Povećavajući ili slabi na svakoj takvoj točki. Zato što cijeli sustav ima aksijalna simetrija, zatim upadni cilindrični snop svjetlosti pretvara se u konusnu, a na ekranu se nalazi i osnosimetrični difrakcijski uzorak izmjeničnih svijetlih i tamnih prstenova, koji se nazivaju i maksimumima i minimumima osvjetljenja. U točki P, koja se nalazi na osi rupe, pojavit će se svijetla točka - glavni maksimum, a prva od sekundarnih maksimuma osvjetljenja pojavit će se u točki Q. Intenzitet sekundarnih maksimuma se smanjuje kako se povećava njihova udaljenost od središta difrakcijskog uzorka. Odnos između veličine rupe i stupnja difrakcije određuje se sljedećom jednadžbom:

sinθ = λ / d, gdje

• θ je kut između smjera prema središtu difrakcijskog uzorka i smjera prema njegovom prvom minimumu,
• λ je valna duljina svjetla.

Donja slika pokazuje kako intenzitet osvjetljenja zaslona varira ovisno o kutnoj udaljenosti od središta. Imajte na umu da su minimumi između sekundarnih maksimuma smješteni na točkama koje su višestruke od ∏.

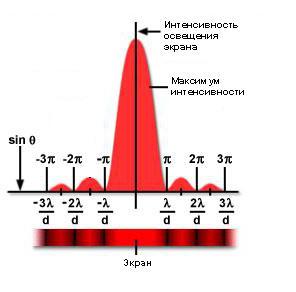
Analitički proračun slike takvog fenomena kao što je Fresnelova difrakcija na rupi i disku značajno je pojednostavljen zbog aksijalne simetrije, o čemu će biti više riječi u daljnjem tekstu.

Okrugli disk na putu snopa svjetlosti

Ako slijedimo Fresnelovu teoriju, onda kada se okrugli neprozirni disk postavi na snop svjetlosti, sve točke na njegovim rubovima postaju izvori koherentnih sekundarnih sfernih valova. Razmaci između tih točaka i točke presjeka osi diska s neprozirnim zaslonom okomito na nju jednaki su. Zbog toga valovi iz svih točaka na rubu diska moraju se presijecati u isto vrijeme iu istoj fazi, tj. Moraju biti presavijeni i značajno ojačati jedan drugog. Pokazalo se da u središtu kružne sjene s diska treba promatrati svijetlo osvijetljeno mjesto, kao na slici ispod. 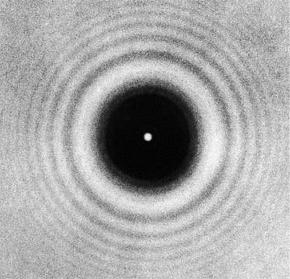Ovu okolnost prvi je uočio francuski fizičar S. Poisson, koji je bio protivnik Fresnelove teorije. Smatrao je da okolnost koju on primjećuje dokazuje svoju nedosljednost. Kakvo je bilo njegovo iznenađenje kada je Fresnel zajedno s Aragoom učinio odgovarajuće iskustvo i dobio takvo mjesto u središtu sjenke s diska! Donja slika shematski prikazuje ovo iskustvo.

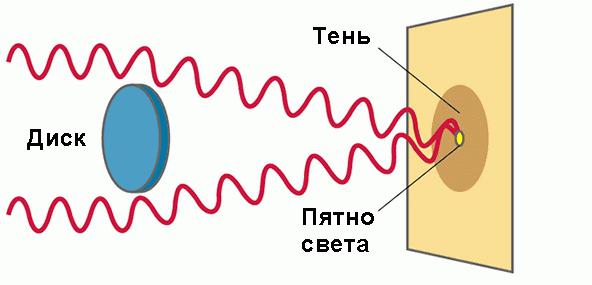
Tako se Fresnelova difrakcija manifestira na disku. Svijetla točka u središtu njezine sjene dobila je ime Poissonova mjesta. Ako je disk mali, onda je intenzitet svjetla u središtu njegove difrakcijske slike gotovo isti kao i kod njegove (disk) odsutnosti.

Kako izračunati difrakcijske uzorke

U općem slučaju, teško je izračunati interferenciju sekundarnih valova kako bi se dobio difrakcijski uzorak. Ali u osi-simetričnim slučajevima može se pojednostaviti, tako da cijela slika fenomena difrakcije postane jednostavna. Metoda Fresnelovih zona omogućuje vizualno geometrijski način razbijanja prednjeg dijela sfernog vala u kružne dijelove.

Amplitude i relativne faze svih zona uzimaju se u obzir za izračunavanje raspodjele intenziteta. Stoga se za određivanje difrakcijskog uzorka koristi prilično složena matematička obrada. Ali kada analiziramo takvu pojavu kao što je Fresnelova difrakcija na okruglom otvoru i disku, ona je uvelike pojednostavljena.

Na donjoj slici S je točkasti izvor svjetla. 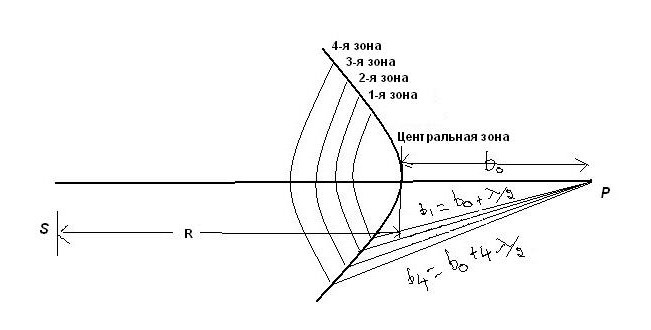S emitira sferični svjetlosni val duljine λ u smjeru s lijeva na desno. Neka radijus njezine fronte u vremenu t bude jednak R. Učinak ovog fronta vala u točki P određuje se dijeljenjem u kružne zone. Udaljenost od rubova dviju uzastopnih zona do točke P razlikuje se za λ / 2. Zona zvona s ovim svojstvom naziva se Fresnelovim zonama. Udaljenost od nule do točke P je b ₀ .

Prva zona je na udaljenosti b ₁ = b ₀ + λ / 2; drugi: b ₂ = b ₀ + 2λ / 2; treće: b ₃ = b ₀ + 3λ / 2; i-ta zona: b _i = b ₀ + iλ / 2.

Uzastopni rubovi dvaju susjednih zona nalaze se na sličnim točkama. Ako se u njima pobuđuju sekundarni sferični valovi, oni dolaze do točke promatranja P s faznom razlikom od 180 ° i međusobno se slabe kada se prekriju (ali ne i unište).

Fresnelova difrakcija na kružnoj rupi i disku - slika s aksijalnom simetrijom. Stoga, korištenje ove metode može značajno pojednostaviti konstrukciju difrakcijskog uzorka kada svjetlost prolazi kroz takve prepreke.

Kako zona Fresnelovog prstena radi na okrugloj rupi?

Razmotrimo opet slučaj kada se difrakcija svjetlosti dogodi na okruglom otvoru. Fresnelove zone u koje se može razbiti prednji val, polaganje u rupu određenog promjera na određenoj valnoj duljini λ i udaljenost od prednjeg prema zaslonu ₀ , mogu biti u količini izraženoj neparnim ili parnim brojem. Kao što je već navedeno, sekundarni valovi iz dvije susjedne zone u svakoj točki zaslona slabe, iako se međusobno ne uništavaju. Stoga, ako je za središte difrakcijskog uzorka broj Fresnelovih zona koje se uklapaju u rupu neparan (2k + 1), tada će amplituda osvjetljenja u središtu slike biti zbroj ostatka prve (središnje) zone i ništa kompenzirano (2k + 1) - zone koje će se međusobno pojačati. Difrakcijski uzorak za ovaj slučaj prikazan je na slici ispod.

Ako je broj Fresnelovih zona složenih u rupi jednak, tada će se utjecaj svih zona u središtu slike međusobno kompenzirati u parovima, au njemu će se pojaviti tamna mrlja.