Kako izračunati volumen različitih geometrijskih tijela?
Tijekom stereometrije jedno od glavnih pitanja je kako izračunati volumen određenog geometrijskog tijela. Sve počinje jednostavnim paralelopipedom i završava se loptom.
U životu, također, često moraju rješavati slične probleme. Na primjer, za izračunavanje količine vode koja se stavlja u kantu ili bačvu.
Svojstva poštena prema volumenu svakog tijela
- Ova vrijednost je uvijek pozitivan broj.
- Ako se tijelo može podijeliti na dijelove tako da nema sjecišta, tada je ukupni volumen jednak zbroju volumena dijelova.
- Jednaka tijela imaju isti volumen.
- Ako se manje tijelo potpuno uklopi u veći, tada je volumen prvog manji od drugog.
Opće oznake za sva tijela
U svakoj od njih nalaze se rubovi i podnožja u kojima se grade visine. Stoga su takvi elementi za njih jednako označeni. Tako se pišu u formulama. Kako izračunati volumen svakog tijela - naučit ćemo dalje i primijeniti nove vještine u praksi.
| oznaka | razjašnjenje |
| i | rub tijela gdje su svi jednaki |
| V | volumen |
| S0 | osnovno područje |
| h | visinu |
| r | radius |
Neke formule imaju i druge vrijednosti. O njihovom imenovanju raspravljat će se kada se pojavi takva potreba.
Prizma, paralelopiped (ravna i kosa) i kocka
Ta su tijela kombinirana jer izgledaju vrlo slično, a formule za izračunavanje volumena su identične:
V = S 0 * h.
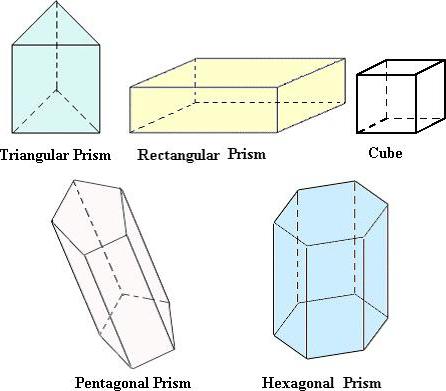
Samo će se S0 razlikovati. U slučaju paralelepipeda, izračunava se kao za pravokutnik ili kvadrat. U prizmi, baza može biti trokut, paralelogram, proizvoljni četverokut ili drugi poligon.
Za kocku je formula znatno pojednostavljena, jer su sve njene dimenzije jednake:
V = a 3 .
Piramida, tetraedar, krnja piramida
Za prvo od ovih tijela postoji takva formula za izračunavanje volumena:
V = 1/3 * S 0 * n.
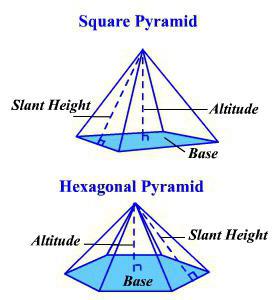
Tetraedar je poseban slučaj trokutaste piramide. Svi rubovi su jednaki. Stoga opet dobivamo pojednostavljenu formulu:
V = (a3 * )2) / 12, ili V = 1/3 S0 h
Skraćena piramida postaje kad je njen gornji dio odrezan. Stoga je njegov volumen jednak razlici između dvije piramide: one koja bi bila netaknuta i udaljenog vrha. Ako je moguće saznati obje baze takve piramide (S 1 je veća i S 2 je manja), onda je prikladno koristiti ovu formulu za izračunavanje volumena:
V = 1/3 * h * (S1 + √ (S1S2) + S2).
Cilindar, konus i krnji stožac
Ako želite izračunati volumen spremnika Možete koristiti formulu koja je specificirana za prizmu. Ponekad je prikladno pisati u ovom obliku:
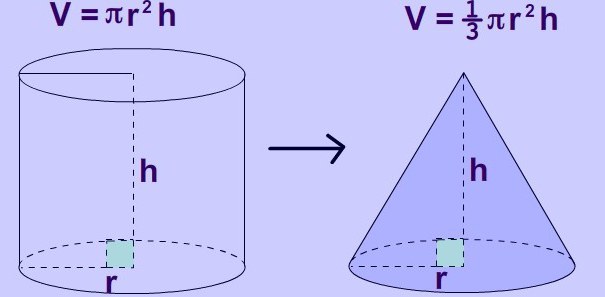
V = π * r 2 * h.
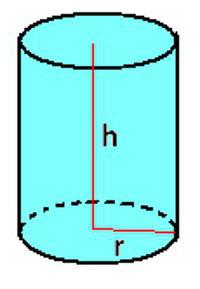
Situacija s konusom nešto je složenija. Za njega postoji formula:
V = 1/3 π * r 2 * h. Vrlo je slična onoj za cilindar, samo se vrijednost smanjuje tri puta.
Kao i kod skraćene piramide, situacija nije jednostavna s konusom koji ima dvije baze. Formula za izračunavanje volumena krnjeg stošca je sljedeća:
V = 1/3 π * h * (r 1 2 + r 1 r 2 + r 2 2 ). Ovdje je r 1 polumjer donje baze, r2 je gornji (manji).
Ball, segmenti lopte i sektor
Te formule su najteže zapamtiti. za volumen lopte izgleda ovako:
V = 4/3 π * r 3 .
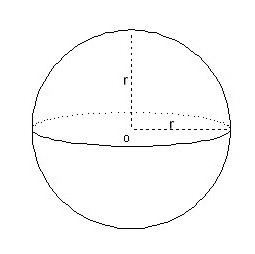
U problemima se često postavlja pitanje kako izračunati volumen sfernog segmenta - dio kugle koja je, kako je bilo, izrezana paralelno s promjerom. U tom slučaju, spašava se sljedeća formula:
V = π h 2 * (r - h / 3). U njemu, za h, uzima se visina segmenta, odnosno dio koji ide uzduž radijusa lopte.
Sektor je podijeljen u dva dijela: konus i segment lopte. Stoga se njegov volumen definira kao zbroj tih tijela. Formula nakon transformacije izgleda ovako:
V = 2/3 πr 2 * h. Ovdje je h također visina segmenta.
Primjeri zadataka
Volumeni cilindra, lopte i konusa
Stanje: promjer cilindra (1 tijelo) jednak je njegovoj visini, promjeru kuglice (2 tijela) i visini stožca (3 tijela); provjeriti proporcionalnost volumena V 1 : V 2 : V 3 = 3: 2: 1
Odluka. Prvo, morate napisati tri formule za volumene. Zatim uzmite u obzir da je polumjer pola promjera. To znači da će visina biti jednaka dva radijusa: h = 2r. Nakon jednostavne zamjene, ispada da će formule za volumene izgledati ovako:
V 1 = 2 π r 3 ; V 3 = 2/3 π r 3 . Formula za volumen lopte se ne mijenja, jer se u njoj visina ne pojavljuje.
Sada ostaje pisanje odnosa volumena i smanjenje 2π i r3. Ispada da je V 1 : V 2 : V 3 = 1: 2/3: 1/3. Ovi brojevi lako vode do zapisa 3: 2: 1.
Odgovor je. V 1 : V 2 : V 3 = 3: 2: 1.
O glasnoći lopte
Stanje: postoje dvije lubenice radijusa 15 i 20 cm; Koji je najpovoljniji način da ih pojedete: prva četiri ili drugi od njih?
Odluka. Da biste odgovorili na ovo pitanje, morate pronaći omjer volumena komada koji će dobiti od svake lubenice. Uzimajući u obzir da su to loptice, morate napisati dvije formule za svezak. Zatim uzmite u obzir da će od prvog dobiti samo četvrti dio, a od drugog - osmi.
Ostaje da se zabilježi omjer volumena dijelova. Izgledat će ovako:
(V 1 : 4) / (V 2 : 8) = (1/3 π r 1 3 ) / (1/6 π r 2 3 ). Nakon pretvorbe ostaje samo frakcija: (2 r 1 3 ) / r 2 3 . Nakon zamjene vrijednosti i proračuna dobivena je frakcija 6750/8000. Iz nje je jasno da će dio iz prve lubenice biti manji nego iz drugog.
Odgovor je. Isplativije je jesti osmi dio lubenice u radijusu od 20 cm.
O volumenu piramide i kocke
Stanje: tu je piramida od gline s pravokutnom podlogom 8x9 cm i visinom od 9 cm; iz istog su gline napravili kocku; Kakav je njegov rub?
Odluka. Ako označimo strane pravokutnika slovima ui sa, onda se površina baze piramide računa kao njihov proizvod. Zatim formulu za njen volumen:
V 1 = 1/3 * sunce * h.
Formula za volumen kocke napisana je u gornjem članku. Ove dvije vrijednosti su jednake: V 1 = V 2 . Ostaje ravnati se s desnim stranama formula i izvesti potrebne izračune. Ispada da je rub kocke jednak 6 cm.
Odgovor je. a = 6 cm
O volumenu paralelepipeda
Stanje: potrebno je izraditi kutiju kapaciteta 0,96 m 3 , poznatu širinu i dužinu - 1,2 i 0,8 metara; Koja bi trebala biti njegova visina?
Odluka. Budući da je baza paralelopipeda pravokutnik, njegovo područje je definirano kao produkt duljine (a) i širine (c). Stoga formula za volumen izgleda ovako:
V = a * c * n.
Iz nje je lako odrediti visinu dijeljenjem glasnoće s područjem. Ispada da visina treba biti jednaka 1 m.
Odgovor je. Visina kutije je jedan metar.