Kako provesti cjelovitu funkcijsku studiju

U ovom članku razmotrit ćemo shemu za proučavanje funkcije, a također ćemo dati primjere studija o ekstremima, monotonosti i asimptotama ove funkcije.

shema

1. Funkcija područja postojanja (DHS).
2. Sjecište funkcije (ako postoji) s osima koordinata, znakovima funkcije, parnosti, periodičnosti.
3. Prekidi (njihov rod). Kontinuitet. Vertikalne asimptote.
4. Monotonija i ekstremne točke.
5. Točke infleksije Izbočina.
6. Proučavanje beskonačne funkcije na asimptotama: horizontalno i koso.
7. Iscrtavanje.

Studija monotonije

Teorem. Ako je funkcija g kontinuirana na [a, b] , diferencirana s (a; b) i g '(x) ≥ 0 (g' (x) ≤0 ) , xê (a; b) , tada se g povećava (smanjuje) za [a, b] .

primjer:

y = 1: 3x3 - 6: 2x2 + 5x.

DHS: xR

y '= x ² + 6x + 5.

Pronađi intervale konstantnih znakova y ' . Budući da je y elementarna funkcija, može promijeniti znakove samo na mjestima gdje se okreće na nulu ili ne postoji. Njezin DHS: xR .

Pronađite točke, čiji je derivat 0 (nula):

y '= 0;

x = -1; -5.

Dakle, y raste na (-∞; -5] i na [-1; + ∞), y spuštanjem na [1; 2] .

Ekstremna studija

T. x _{0 se} naziva maksimalnom točkom (max) na skupu A funkcije g kada se vrijednost g (x ₀ ) ≥ g (x), xêA , uzme kao funkcija u toj točki.

T. x ₀ naziva se minimalna točka (min) funkcije g na skupu A kada se kao funkcija u ovoj točki uzme najmanji g (x ₀ ) ≤ g (x), xêA.

Na skupu A maksimalne točke (max) i minimum (min) nazivaju se ekstremnim točkama g . Takvi ekstremi se također nazivaju apsolutnim ekstremima na skupu ,

Ako je x ₀ ekstremna točka g u nekom području, tada se x ₀ naziva lokalna ili lokalna točka ekstrema (max ili min) od g.

Teorem (uvjet potreban). Ako je x ₀ ekstremna točka (lokalne) funkcije g , tada derivat ne postoji ili je jednak u ovoj r. 0 (nuli).

Definicija. Kritične točke su točke s nepostojećim ili jednakim 0 (nultim) derivatom. Ove točke podataka su sumnjive za ekstrem.

Teorem (uvjet br. 1). Ako je funkcija g kontinuirana u određenom susjedstvu t. X ₀ i znak mijenja svoj derivat na prijelazu, tada je zadana točka ekstrema g .

Teorem (uvjet br. 2). Neka se funkcija u određenom distriktu diferencira dva puta i g '= 0, i g' '> 0 (g' '<0) , onda ova točka je točka maksimalne (max) ili minimalne (min) funkcije.

Studija ispupčenja

Funkcija se naziva konveksna dolje (ili konkavna) na intervalu (a, b) kada grafikon funkcije nije veći od sekanta na intervalu za bilo koji x sa (a, b) koji prolazi kroz te točke .

Funkcija će biti konveksna strogo dolje na (a, b) , ako - grafikon leži ispod sekanta na razmaku.

Funkcija se naziva konveksna (konveksna) na intervalu (a, b) , ako je za bilo koje t- točke s (a, b) graf funkcije na intervalu nije niži od sekanta koji prolazi kroz apscise u tim točkama ,

Funkcija će biti strogo konveksna prema gore na (a, b ), ako - graf na intervalu leži iznad sekanta.

Ako je funkcija u okrugu točka je kontinuirana i nakon t. x ₀ funkcija mijenja konveksnost na prijelazu, a ta se točka naziva točka infleksije funkcije.

Asimptotni test

Definicija. Pravac se naziva asimptot g (x) ako se na beskonačnoj udaljenosti od izvora koordinata približava točka funkcije grafova: d (M, l).

Asimptote mogu biti okomite, vodoravne i ukošene.

Okomita crta s jednadžbom x = x ₀ bit će asimptota vertikalnog grafa funkcije g ako u t. x _{0 je} beskonačni jaz, tj. barem jedna lijeva ili desna granica u ovom trenutku je beskonačnost.

Proučavanje funkcije na segmentu na vrijednosti najmanjih i najvećih

Ako je funkcija kontinuirana na [a, b] , tada prema Weierstrassovom teoremu postoji najveća vrijednost i najmanja vrijednost na tom segmentu, to jest, postoje točke koje pripadaju [a, b] tako da je g (x ₁ ) ≤ g (x) <g (x2), x2e [a, b]. Iz teorema o monotonosti i ekstremima dobivamo sljedeću shemu za proučavanje funkcije na segmentu za najmanju i najveću vrijednost.

plan

1. Pronađite derivat g '(x) .
2. Na ovim mjestima i na krajevima segmenta pronađite vrijednost funkcije g .
3. Pronađene vrijednosti uspoređuju i odabiru najmanju i najveću.

Napomena. Ako želite proučiti funkciju na konačnom intervalu (a, b) ili na beskonačnom (-∞; b); (-∞; + ∞) na max i min vrijednosti, zatim u planu, umjesto vrijednosti funkcije na krajevima razmaka, pretražuju se odgovarajuće jednostrane granice: umjesto f (a), f (a +) = limf (x) se traži , umjesto f (b), f (b). Tako možete pronaći LDU funkcije na intervalu, jer apsolutni ekstremi ne moraju nužno postojati u ovom slučaju.

Primjena izvedenice na rješavanje primjenjenih problema na ekstremu pojedinih veličina

1. Izrazite ovu vrijednost u smislu drugih vrijednosti iz stanja problema tako da je funkcija samo jedne varijable (ako je moguće).
2. Odredite razdoblje promjene ove varijable.
3. Provesti proučavanje funkcije na intervalu pri maksimalnim i min vrijednostima.

Zadatak. Potrebno je izgraditi pravokutnu platformu, koristeći rešetkaste metre, uz zid tako da se s jedne strane uklapa u zid, a na ostale tri je ograđena rešetkom. U kojem će omjeru najveće biti područje takvog mjesta?

S = xy je funkcija 2 varijable.

S = x (a - 2x) - funkcija 1. varijable ; x ê [0; a: 2].

S = ax - 2x2; S '= a - 4x = 0, xêR, x = a: 4.

S (a: 4) = a ² : 8 je najveća vrijednost;

S (0) = 0.

Pronađite drugu stranu pravokutnika: = a: 2.

Omjer slike: y: x = 2.

Odgovor je. Najveća površina će biti jednaka 2/8 , ako je strana koja je paralelna sa zidom 2 puta veća od druge strane.

Funkcija istraživanja. primjeri

Primjer 1

Postoji y = x ³ : (1-x) ² . Izvršite istraživanje.

1. DHS: xê (-∞; 1) U (1; ∞).
2. Opći oblik funkcije (čak ni neparan) nije simetričan u odnosu na točku 0 (nula).
3. Znakovi funkcije. Funkcija je elementarna, tako da može mijenjati znak samo na mjestima gdje je 0 (nula) ili ne postoji.
4. Funkcija je elementarna, dakle kontinuirana na DHS-u: (-∞; 1) U (1; ∞).

Gap: x = 1;

limx ³ : (1 - x) ² = ∞ - diskontinuitet druge vrste (beskonačan), tako da u točki 1 postoji vertikalna asimptota;

x = 1 je vertikalna asimptotska jednadžba.

5. y '= x2 (3-x): (1 - x) ³ ;

DHS (y '): x; 1;

x = 1 - kritična točka.

y '= 0;

0; 3 - kritične točke.

6. y "= 6x: (1 - x) ⁴ ;

Kritična t: 1, 0;

x = 0 - m. kink, y (0) = 0.

7. limx ³ : (1 - 2x + x ² ) = ∞ - nema horizontalne asimptote, ali može biti nagnuta.

k = 1 je broj;

b = 2 je broj.

Prema tome, postoji asimptota nagnuta y = x + 2 na + ∞ i na - ∞.

Primjer 2

S obzirom na y = (x ² + 1): (x - 1). Za istraživanje i istraživanje. Izradite grafikon.

1. Područje postojanja je cijela numerička linija, osim m. X = 1 .

2. y presijeca OY (ako je moguće) u m. (0; g (0)) . Nađi y (0) = -1 - t. raskrižje OY ,

Točke presijecanja grafa s OX nalazimo rješavanjem jednadžbe y = 0 . Korenska jednadžba nema valjanosti, stoga ova funkcija ne siječe OX .

3. Funkcija nije periodična. Razmotrite izraz

g (-x) (g (x), i g (-x) -g (x) . To znači da je to generička funkcija (ni čak ni neparna).

4. T. x = 1 jaz ima drugu vrstu. U svim ostalim točkama funkcija je kontinuirana.

5. Proučavanje funkcije na ekstremu:

(x ² - 2x - 1): (x - 1) ² = y '

i riješiti jednadžbu y '= 0.

Dakle, 1 - ,2, 1 + √2, 1 - kritične točke ili točke mogućeg ekstrema. Te točke dijele numeričku liniju na četiri intervala .

U svakom intervalu derivat ima određeni znak, koji se može postaviti metodom intervala ili izračunavanjem vrijednosti izvedenice na pojedinim točkama. Na intervalima (-∞; 1 - ) 2 ) U ( 1 + ; 2 ; ∞) pozitivni derivat znači da funkcija raste; ako je xê ( 1 - ; 2 ; 1) U (1; 1 + √2 ) , funkcija se smanjuje, jer je u tim intervalima derivat negativan. Kroz t X ₁ kada idete (pomicanjem s lijeva na desno) mijenjate izvedeni znak iz "+" u "-", dakle, u ovom trenutku postoji lokalni maksimum, nalazimo

y _max = 2 - 2 .2 .

Kada prolazite kroz x _{2, on} mijenja izvedeni znak iz "-" u "+", stoga u ovom trenutku postoji lokalni minimum i

y _mix = 2 + 2√2.

T. x = 1 nije tako ekstreman.

6. 4: (x - 1) ³ = y ".

U (-∞; 1 ) 0> y ' , dakle, na tom intervalu krivulja je konveksna; ako je xê ( 1 ; ∞) - krivulja je konkavna. U točki 1, funkcija nije definirana, stoga ova točka nije točka infleksije.

7. Iz rezultata stavka 4 slijedi da je x = 1 vertikalna krivulja asimptote.

Horizontalne asimptote su odsutne.

x + 1 = y je asimptota koja je nagnuta ovom krivuljom. Nema drugih asimptota.

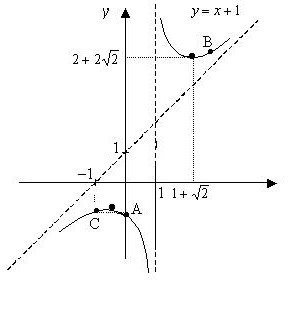
8. S obzirom na provedeno istraživanje gradimo graf (vidi sliku iznad).