Kako pronaći trg s dijamantima? Mogući načini pronalaženja odgovora

Matematika je školski predmet koji svi uče, bez obzira na profil razreda. Međutim, svatko je ne voli. Ponekad nepravedno. Ova znanost neprestano baca studente na zadatke koji dopuštaju razvoju mozga. Matematika se snalazi kako se dječje mentalne sposobnosti ne bi izblijedile. Jedan od njezinih odjeljaka se s tim osobito dobro nosi - geometrija.

Bilo koja od tema koje se proučavaju u njoj zaslužuje pažnju i poštovanje. Geometrija je način za razvoj prostorne imaginacije. Primjer je tema kvadrata figura, posebno dijamanata. Ove zagonetke mogu dovesti do slijepe ulice, ako ne razumijete detalje. Zato što su mogući različiti pristupi pronalaženju odgovora. Netko je lakše zapamtiti različite verzije formula koje su napisane ispod, a netko ih može dobiti iz prethodno naučenog materijala. U svakom slučaju, beznadne situacije se ne događaju. Ako mislite malo, rješenje će sigurno biti pronađeno.

Što je romb i kako to izgleda kao drugi kvadrilaterali?

Odgovorite na ovo pitanje kako biste razumjeli principe dobivanja formula i tijek rasuđivanja u problemima. Uostalom, kako bi shvatili kako pronaći područje romba, morate jasno razumjeti kakva je to figura i kakva su njezina svojstva.

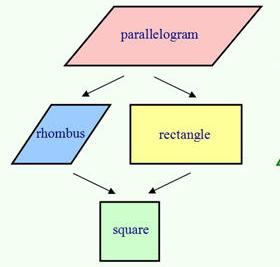
Za praktičnost razmatranja paralelograma, koji je četverostrana s parnim paralelnim stranama, uzet ćemo "roditelja". Ima dva "djeteta": pravokutnik i romb. Oba su paralelogrami. Ako nastavimo paralele, ovo je "prezime". Dakle, da bi pronašli romb Možete koristiti već proučenu formulu paralelograma.

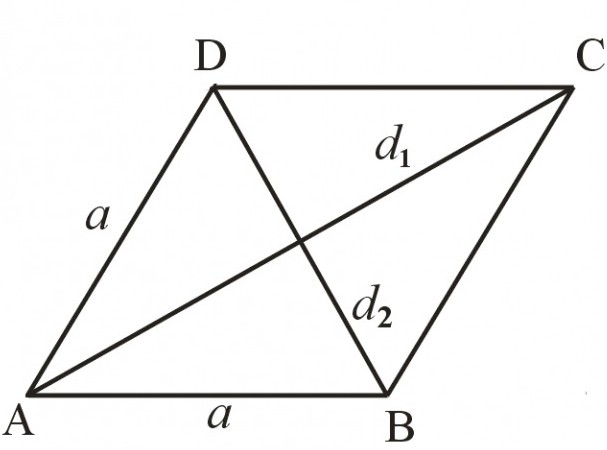
Ali, kao i sva djeca, romb ima nešto svoje. To se malo razlikuje od "roditelja" i može se smatrati zasebnom figurom. Uostalom, pravokutnik nije romb. Vraćajući se na paralele - oni su poput brata i sestre. Imaju mnogo toga zajedničkog, ali se i dalje razlikuju. Ove razlike su njihova posebna svojstva koja se trebaju koristiti. Bilo bi čudno znati o njima i ne primjenjivati ​​u rješavanju problema.

Ako nastavimo analogiju i zapamtimo još jednu figuru - kvadrat, onda će to biti nastavak romba i pravokutnika. Ova brojka objedinjuje sva svojstva jednog i drugog.

Dijamantna svojstva

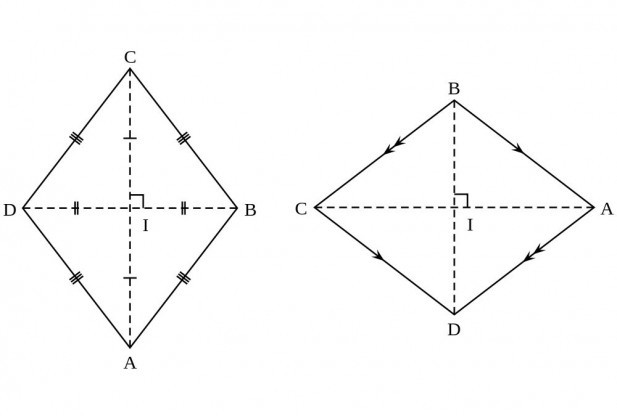
Ima ih pet i navedeni su u nastavku. A neki od njih ponavljaju svojstva paralelograma, a neki su svojstveni samo onoj slici.

• Romb je paralelogram koji je poprimio poseban oblik. Iz toga slijedi da su njegove strane parano paralelne i jednake. Štoviše, oni su u parovima nejednaki, a to je sve. Kao što bi imao kvadrat.
• Dijagonale ovog četverokuta sijeku se pod kutom jednakim 90º. To je zgodno i uvelike pojednostavljuje tijek rasuđivanja pri rješavanju problema.
• Još jedno svojstvo dijagonala: svaka od njih je podijeljena točkom sjecišta na jednake segmente.
• Kutovi koji leže jedan nasuprot drugome jednaki su.
• I posljednje svojstvo: dijagonala romba se podudara s simetralima kutova.

Oznake koje se prihvaćaju u razmatranim formulama

U matematici je potrebno riješiti probleme pomoću zajedničkih izraza slova, koji se nazivaju formulama. Tema trga nije iznimka.

Da biste otišli na zapise koji govore kako pronaći područje dijamanta, morate se složiti oko slova koja zamjenjuju sve numeričke vrijednosti elemenata slike.

Sada je vrijeme za pisanje formula.

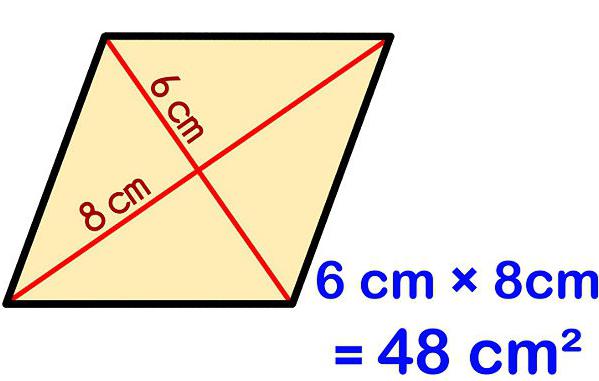
Među podacima o zadatku postoje samo dijagonalni dijamanti.

Pravilo kaže da je za pronalaženje nepoznate količine potrebno pomnožiti duljine dijagonala, a zatim podijeliti proizvod na pola. Rezultat podjele je područje romba preko dijagonala.

Formula za ovaj slučaj će izgledati ovako:

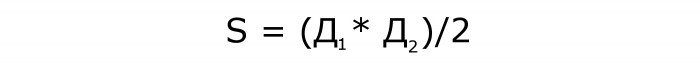
Neka ova formula ide na broj 1.

Zadatak se daje strani dijamanta i njegovoj visini

Da biste izračunali površinu, morate pronaći proizvod ove dvije količine. Možda je to najjednostavnija formula. Osim toga, poznato je iz teme o području paralelograma. Tamo je takva formula već proučavana.

Pisanje matematike:

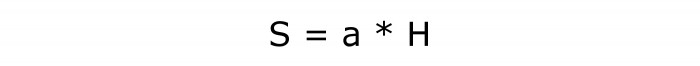
Broj ove formule je 2.

Poznati i oštri kut

U ovom slučaju trebate kvadrirati veličinu rombove strane. Zatim pronađite sinus kuta. I treći korak je izračunati proizvod dvije formirane količine. Odgovor će biti dijamantni trg.

Doslovni izraz:

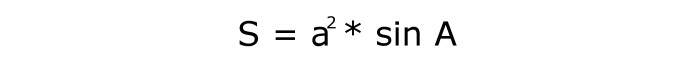
Njegov serijski broj je 3.

Ove vrijednosti: radijus upisane kružnice i akutni kut

Da biste izračunali površinu romba, morate pronaći kvadrat radijusa i pomnožiti ga s 4. Odredite vrijednost sinusa kuta. Zatim podijelite proizvod s drugom količinom.

Formula ima sljedeći oblik:

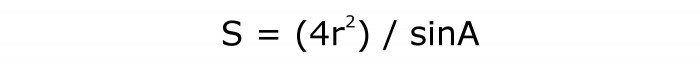
Bit će označen brojem 4.

Problem uključuje stranu i radijus upisane kružnice.

Da biste odredili kako pronaći područje romba, trebate izračunati proizvod tih količina i broj 2.

Formula za ovaj zadatak izgledat će ovako:

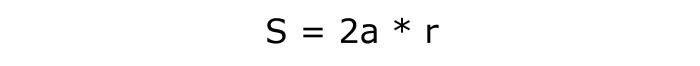
Broj joj je u redu - 5.

Primjeri mogućih zadataka

Zadatak 1

Jedna od dijagonala romba je 8, a druga 14 cm, a potrebno je pronaći područje figure i duljinu njegove strane.

odluka

Da biste pronašli prvu vrijednost, trebate formulu 1, u kojoj je D ₁ = 8, D ₂ = 14. Tada se površina izračunava na sljedeći način: (8 x 14) / 2 = 56 (cm2).

Dijagonale dijele dijamant na 4 trokuta. Svaki od njih bit će pravokutni. Ovo se mora koristiti za određivanje vrijednosti druge nepoznate. Strana romba će postati hipotenuza trokuta, a noge će biti polovica dijagonala.

Zatim ^a2 = (D _1/2 ) ² + (D 2/2) ^2. Nakon što sve vrijednosti zamijenimo, dobivamo: a ² = (8/2) ² + (14/2) ² = 16 + 49 = 65. Ali to je kvadrat na strani. Dakle, morate izvaditi kvadratni korijen od 65. Tada će duljina stranice biti približno jednaka 8,06 cm.

Odgovor: površina je 56 cm ² , a strana 8,06 cm.

Zadatak 2

Dijamantna strana ima vrijednost od 5,5 dm, a visina mu je 3,5 dm. Pronađite područje slike.

odluka

Za pronalaženje odgovora bit će potrebna formula 2. U njoj je a = 5.5, H = 3.5. Zatim, zamjenjujući slova u formuli brojevima, dobivamo da je željena vrijednost 5,5 * 3,5 = 19,25 (dm ² ).

Odgovor: površina romba je jednaka 19,25 dm ² .

Zadatak 3

Akutni kut romba je 60º, a njegova manja dijagonala je 12 cm, a potrebno je izračunati njegovu površinu.

odluka

Da biste dobili rezultat, trebat će vam formula broj 3. U njoj će umjesto A biti 60, a vrijednost a je nepoznata.

Da biste pronašli stranu romba, morate se sjetiti sinusnog teorema. U pravokutnom trokutu, a bit će hipotenuza, manja noga jednaka je polovici dijagonale, a kut je podijeljen na pola (poznat iz svojstva gdje se spominje simetrala).

Tada će strana a biti jednaka proizvodu noge na sinusu kuta.

Noga se mora izračunati kao D / 2 = 12/2 = 6 (cm). Sinus (A / 2) bit će jednak njegovoj vrijednosti za kut od 30º, odnosno 1/2.

Izvođenjem jednostavnih izračuna dobivamo sljedeću vrijednost strane romba: a = 3 (cm).

Sada je površina produkt 3 ² i sinus 60º, to jest, 9 * ()3) / 2 = (9√3) / 2 (cm2).

Odgovor: željena vrijednost je (9√3) / 2 cm2.

Rezultati: sve je moguće

Ovdje su razmatrane neke mogućnosti kako pronaći područje dijamanta. Ako nije jasno u problemu izravno koje formule koristiti, onda morate malo razmisliti i pokušati povezati prethodno proučene teme. U drugim temama uvijek postoji savjet koji će pomoći povezati poznate vrijednosti s onima u formulama. A problem će biti riješen. Glavno je zapamtiti da sve što je prethodno proučeno može i treba biti korišteno.

Osim predloženih zadataka, mogući su i inverzni problemi, kada se na području figure mora izračunati vrijednost dijamantnog elementa. Zatim morate koristiti jednadžbu koja je najbliža uvjetu. Zatim pretvorite formulu, ostavljajući nepoznatu vrijednost na lijevoj strani jednakosti.