Kako pronaći visinu trapeza: formula za sve prilike
Postoji nekoliko odgovora na jednostavno pitanje "Kako pronaći visinu trapeza?", Sve zato što se mogu dati različite početne vrijednosti. Stoga će formule varirati.
Te se formule mogu zapamtiti, ali se lako izvode. Potrebno je samo primijeniti prethodno izučene teoreme.
Prihvaća se formulama
U svim matematičkim zapisima u nastavku, takva čitanja slova su točna.
| proizvoljni trapez | jednakokračan trapez | ime |
| i | i | donja baza |
| u | u | vrh baze |
| c, d | s | strane |
| n | n | visinu |
| m | m | srednja linija |
| d 1 d 2 | d 1 | dijagonalno |
| a | a | područje |
| α, β | α | donji kutovi dna |
| γ, δ | γ, δ | kutovi na sjecištu dijagonala |
U izvornim podacima: sve strane
Da biste pronašli visinu trapeza u općem slučaju, trebate koristiti sljedeću formulu:
n = √ (c2 - (((a - c) 2 + c2 - d2) / (2 (a - c))) 2 ). Broj 1.
Ne najkraće, ali u zadacima je vrlo rijetko. Obično možete koristiti druge podatke.
Formula koja vam govori kako pronaći visinu jednakokračnog trapeza u istoj situaciji mnogo je kraća:
n = c (c2 - (a - c) 2/4). Broj 2
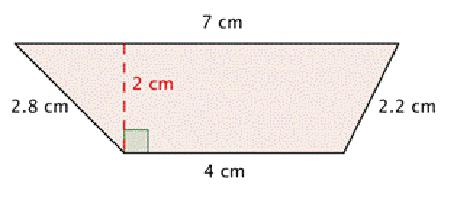
U zadatku su dane: strane i kutovi na dnu baze
Pretpostavlja se da je kut a susjedan strani s oznakom "c", tj. Kut β na strani d. Tada će formula za pronalaženje visine trapeza općenito biti:
n = c * sin α = d * sin β. Broj 3
Ako je broj jednakokračan, možete koristiti ovu opciju:
n = c * sin α = ((a - c) / 2) * tg α. Broj 4
Poznati: dijagonale i kutovi između njih
Tipično, tim se podacima pridružuju još uvijek poznate vrijednosti. Na primjer, osnovna ili srednja linija. Ako su razlozi dani, onda je odgovor na pitanje kako pronaći visinu trapeza koristan u sljedećoj formuli:
n = (d 1 * d 2 * sin γ) / (a + b) ili n = (d 1 * d 2 * sin δ) / (a + b). Broj 5.
Ovo je za cjelokupni izgled slike. Ako je dan izoscen, tada će se zapis pretvoriti na sljedeći način:
n = (d 1 2 * sin γ) / (a + b) ili n = (d 1 2 * sin δ) / (a + b). Broj 6.
Kada se problem bavi središnjom linijom trapeza, formule za pronalaženje njegove visine postaju sljedeće:
n = (d 1 * d 2 * sin γ) / 2m ili n = (d1 * d2 * sin δ) / 2m. Soba 5a.
n = (d 1 2 * sin γ) / 2m ili n = (d 1 2 * sin δ) / 2m. Broj 6a.
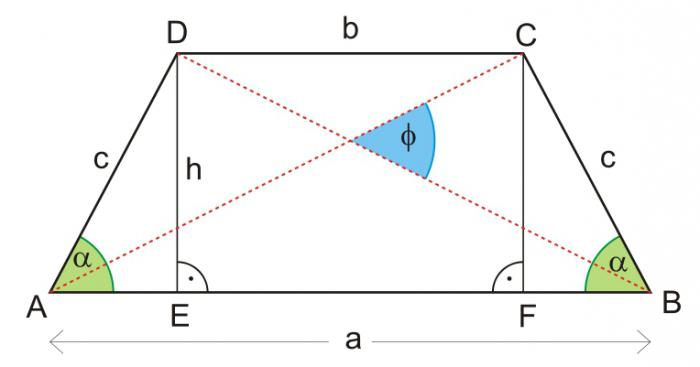
Među poznatim vrijednostima: područje s bazama ili srednjom linijom
To su možda najkraće i najjednostavnije formule za pronalaženje visine trapeza. Za proizvoljan oblik, to će biti:
n = 2S / (a + c). Broj 7.
Isto je, ali s dobro poznatom srednjom linijom:
n = s / m. Soba 7a.
Čudno je, ali za jednakokračan trapezoid, formule će izgledati isto.
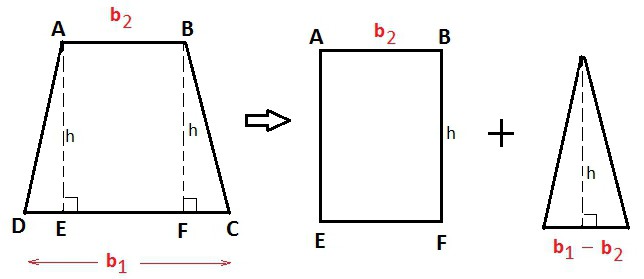
zadaci
№1. O definiciji kutova na dnu trapeza.
Stanje. Daje se jednakokračan trapez, čija je strana 5 cm, a baze su 6 i 12 cm, a potrebno je pronaći sinus akutnog kuta.
Odluka. Radi praktičnosti, trebali biste unijeti zapis. Neka donji lijevi vrh bude A, sve ostalo u smjeru kazaljke na satu: B, C, D. Dakle, donja baza će biti označena kao HELL, gornja baza će biti BC.
Potrebno je nacrtati visine od vrhova B i C. Točke koje označavaju krajeve visina bit će označene kao H1 i H2. Budući da su na slici BCH 1 H 2 svi kutovi ravni, to je pravokutnik. To znači da je segment H1H2 6 cm.
Sada trebamo razmotriti dva trokuta. Jednaki su jer su pravokutni s identičnim hipotenuzama i vertikalnim nogama. Iz toga slijedi da su njihove manje noge jednake. Prema tome, oni se mogu definirati kao kvocijent razlike. Potonji se dobiva oduzimanjem od donje baze gornje. Podijelit će se s 2. To znači da se 12 - 6 mora podijeliti s 2. AN 1 = H 2 D = 3 (cm).
Sada iz Pitagorina teorema trebate pronaći visinu trapeza. Potrebno je pronaći sinus kuta. BH1 = √ (5 2 - 3 2 ) = 4 (cm).
Koristeći spoznaju o tome kako je sinus akutnog kuta u pravokutnom trokutu, možemo napisati sljedeći izraz: sin α = BH 1 / AB = 0.8.
Odgovor je. Željeni sinus je 0,8.
№2. Pronaći visinu trapeza po poznatoj tangenti.
Stanje. Za jednakokračan trapezoid morate izračunati visinu. Poznato je da su njegove baze 15 i 28 cm tangenta akutnog kuta: 11/13.
Odluka. Označavanje vrhova je isto kao u prethodnom zadatku. Opet, morate držati dvije visine iz gornjih kutova. Analogno rješenju prvog problema, potrebno je pronaći AH1 = H2D, koji su definirani kao razlika 28 i 15 podijeljena s dva. Nakon izračuna ispada: 6,5 cm.
Budući da je tangens omjer dvije noge, možemo napisati sljedeću jednakost: tg α = AH 1 / BH 1 . Štoviše, taj omjer je 11/13 (prema stanju). Budući da je AN 1 poznat, moguće je izračunati visinu: VN 1 = (11 * 6.5) / 13. Jednostavni izračuni daju rezultat od 5.5 cm.
Odgovor je. Potrebna visina je 5,5 cm.
№3. Za izračun visine poznatih dijagonala.
Stanje. Poznato je o trapezu da su njegove dijagonale 13 i 3 cm, a potrebno je znati njegovu visinu ako je zbroj baza 14 cm.
Odluka. Neka oznaka figure bude ista kao i prije. Pretpostavimo da je zvučnik manja dijagonala. Iz vrha C morate držati željenu visinu i označiti je CH.
Sada je potrebno izvršiti dodatnu izgradnju. Iz kuta C, morate nacrtati pravac paralelan većoj dijagonali i pronaći točku njegova presjeka s nastavkom strane krvnog tlaka. To će biti D 1 . Ispalo je novi trapezoid, unutar kojeg je nacrtan trokut ASD 1 . To je također potrebno za daljnje rješavanje problema.
Željena visina također će biti u trokutu. Stoga možete koristiti formule proučene u drugoj temi. Visina trokuta definirana je kao proizvod broja 2 i područje podijeljeno stranom na koju je nacrtana. A strana je jednaka zbroju baza izvornog trapeza. To se temelji na pravilu da je izvedena dodatna gradnja.
U trokutu koji se razmatra sve su strane poznate. Radi praktičnosti, unosimo oznaku x = 3 cm, y = 13 cm, z = 14 cm.
Sada možete računati područje, koristeći teorem Gerone. Polu-perimetar će biti p = (x + y + z) / 2 = (3 + 13 + 14) / 2 = 15 (cm). Tada će formula za područje nakon zamjene vrijednosti izgledati ovako: S = √ (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 6 (10 (cm2).
Sada morate brojati visinu: n = (2 * 6) 10) / 14 = 6√10 / 7 (cm).
Odgovor je. Visina je 6√10 / 7 cm.
№4. Tražiti visinu sa strane.
Stanje. Prikazan je trapez, čiji su tri strane 10 cm, a četvrti 24 cm. Trebate znati njegovu visinu.
Odluka. Budući da je lik jednakokračan, tada će vam trebati formula broj 2. U njoj samo trebate zamijeniti sve vrijednosti i računati. Izgledat će ovako:
n = √ (10 2 - (10 - 24) 2/4) = (51 (cm).
Odgovor je. n = 51 cm