Kako pronaći volumen cilindra: formule i problem
Pitanje kako pronaći volumen cilindra može nastati ne samo od učenika. Uostalom, ovaj oblik ima, na primjer, tavu, čiji je kapacitet ponekad hitno potreban da bi se to saznalo. Tada trebate poznavanje posebne formule.
Što trebate znati o cilindru?
Geometrijsko tijelo o kojem govorimo je oblikovano okretanjem pravokutnika oko jedne njegove strane, i uvijek će biti ravno. To jest, kut između generatora cilindra i njegove baze u ovom slučaju je 90 stupnjeva. Ako to jednostavno kretanje ne uspije, a kut više nije 90 stupnjeva, onda govorimo o nagnutom cilindru.
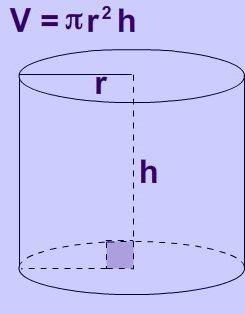
Bez obzira na izgled tijela, još uvijek morate znati kako ga pronaći volumen spremnika. Ali prvo morate odlučiti o nekim teoretskim podacima.
Kako se nazivaju pojedini elementi cilindra i što se o njima zna?
Segmenti koji se u parovima povezuju s odgovarajućim točkama na dvije baze nazivaju se generatori. U svakom su cilindru jednake i paralelne jedna s drugom. Ako je ravna, onda se duljina tvorbe podudara s visinom tijela.
Kružnica ili elipsa može ležati na bazi, a cilindar će biti kružan ili eliptičan. U formulama se ta činjenica mora uzeti u obzir. Zato što se najčešće daju za kružni cilindar. U eliptičkom, prije izračunavanja volumena cilindra, trebat ćete saznati po kojoj formuli odrediti područje ovala.
Formule za volumen ravnih i kosih cilindara
U daljnjem tekstu se uzimaju takve oznake.
| Oznaka slova | matematička količina |
| V | volumen |
| S | osnovno područje |
| h | visinu |
| r | radijus kruga |
| l | generatrix duljine |
| α | kut između generatora i baze |
U svakom slučaju, trebat će vam formula u kojoj se visina tijela množi s područjem baze. Izgleda ovako:
V = Sh
Ako želite saznati kako pronaći volumen ravnog cilindra, onda se ovdje visina duž duljine potpuno poklapa s generatorom. Osnova je najčešće krug, a zatim će se njezina površina izračunati po formuli:
S = πr.
Kada je problem oko eliptičnog cilindra, potrebna je sljedeća formula za područje baze:
S = π ab , ovdje slova a i b označavaju manje i glavne poluosovine ovala.
Prilikom rješavanja problema na nagnutom cilindru morat ćete unijeti neke dodatke u formulu. Na primjer, ako visina nije poznata, ali je riječ o generatoru i kutu između njega i baze. Tada će slovo h trebati zamijeniti takvim izrazom:
h = l * sin α .
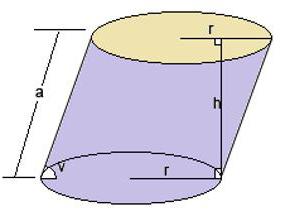
Što ako trebate odrediti volumen u praksi?
U problemima su vrijednosti kuta ili visine s generatorom obično već poznate. A možda i neke druge elemente kroz koje se mogu naći. U životu morate sami obaviti mjerenja.
Zatim se pitanje kako odrediti volumen cilindra svodi na ispravno mjerenje njegove visine i radijusa. Da biste to učinili, trebat će vam: ravnalo, olovka i pravokutni list papira.
U svakodnevnom životu najčešće smo okruženi pravim kružnim cilindrima. Izmjerite njihovu visinu obično nije teško. Vi samo trebate pričvrstiti ravnalo na stranu i izmjeriti udaljenost od dna do vrha tijela. To će biti visina - h.
S radijusom kruga, sve nije tako jednostavno. Moramo zapamtiti malo geometrije. Ovdje vam je potreban list papira s pravim kutom i olovkom.
Što daje teorija geometrije? oko pravokutni trokut Možete opisati krug. Štoviše, njegov pravi kut će biti na njemu, a hipotenuza će se podudarati s promjerom.
Morate uzeti list papira i staviti ga tako da pravi kut dodiruje rub baze. Tada će njegove dvije strane, koje čine ovaj kut, u nekim točkama presjeći krug. Na tim ćete mjestima morati napraviti oznake. Na njima provesti segment. To će biti hipotenuza i željeni promjer baze cilindra.
Kako pronaći volumen cilindra, u našem slučaju? Formula sadrži radijus. Ona je jednaka polovici promjera. To jest, duljina rezultirajućeg segmenta treba biti podijeljena u dvije.
Ostaje samo zamjena rezultata mjerenja u formuli za volumen i brojanje. I uzmite u obzir da je odgovor u cm3. Ako volumen treba biti poznat u kubičnim metrima, tada će broj morati biti podijeljen s milijun. Da bi dobili volumen u litrama, djelitelj će biti tisuću.
zadatak
Stanje. Dva cilindra. Visina prva dva puta u drugom. Polumjer drugog je dvostruko veći od prvog. Potrebno je utvrditi koliko puta je volumen prvog cilindra veći ili manji od volumena drugog.
Odluka. Prvo morate unijeti zapis. Neka visina i radijus prvog tijela budu indeks 1, a drugi - 2.
Sada možete upisati podatke u vrijednosti uvjeta u obliku izraza:
h 1 = 2h2 i r2 = 2r1.
Formule za volumene oba cilindra izgledat će ovako:
v 1 = π r 1 2 h 1 i v 2 = π r 2 2 h 2 .
Zadatak zahtijeva:
v 1 : v 2 = (π r 1 2 h 1 ): (π r 2 2 h 2 ).
Nakon smanjenja π i zamjene h 1 i r 2 unesenim izrazima, ispada:
v 1 : v2 = (r 1 2 2 h 2 ): (4r 1 2 h 2 ).
To je, v 1 : v 2 = 1: 2. To znači da je volumen prvog cilindra dva puta manji.
Odgovor je. v 1 = v 2 : 2.