Uvod u dinamičko programiranje

Među problemima riješenim uz pomoć matematičkog programiranja možemo izdvojiti zasebnu klasu problema koja zahtijeva optimizaciju višestupanjskih (višestupanjskih) procesa. Takvi se zadaci razlikuju po sposobnosti da se rješenje podijeli na nekoliko međusobno povezanih koraka. Za rješavanje takvih problema koristi se dinamičko programiranje ili, kako se još naziva, višestupanjsko programiranje. Njegove su metode optimizirane za pronalaženje optimalnog rješenja višestepenih problema, koji se mogu podijeliti u nekoliko faza, koraka itd.

Podrijetlo izraza

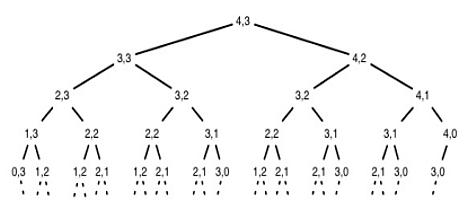
Upotreba riječi "dinamički" u naslovu u početku je podrazumijevala da će se podjela na podzadatke odvijati uglavnom u vremenu. Kada se koriste dinamičke metode za rješavanje proizvodnih, poslovnih i drugih zadataka koji uključuju vremenski faktor, razbijanje u odvojene faze nije teško. No, moguće je koristiti tehniku ​​dinamičkog programiranja u zadacima gdje pojedine faze nisu vremenski povezane. Uvijek u višestupnom zadatku, možete odabrati parametar ili svojstvo, prema kojem možete podijeliti u zasebne korake.

Algoritam (metoda) za rješavanje višestupanjskih problema

Algoritam ili Metoda dinamičkog programiranja temelji se na načelu sekvencijalne optimizacije problema, kada je rješenje općeg problema podijeljeno na niz rješenja pojedinačnih podzadataka s naknadnom integracijom u jedno rješenje. Vrlo često su pojedini podzadaci isti, a jedno uobičajeno rješenje značajno smanjuje vrijeme izračuna. 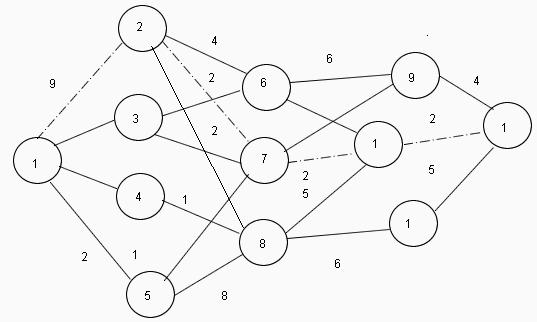Značajka metode je autonomnost rješavanja problema u svakom odvojenom stupnju, tj., Bez obzira na to kako je proces optimiziran i riješen u prethodnom stupnju, trenutni izračun koristi samo procesne parametre koji ga karakteriziraju u ovom trenutku. Na primjer, vozač koji vozi na cesti odlučuje o trenutnom skretanju bez obzira na to koliko je ili koliko je prije vozio.

Metoda iznad i metoda u nastavku

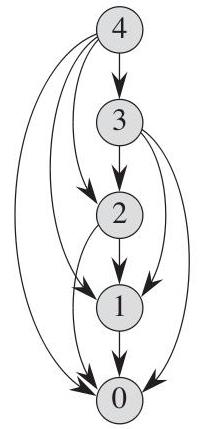
Unatoč činjenici da se pri izračunu u odvojenom stupnju rješavanja problema koriste procesni parametri za trenutni trenutak, rezultat optimizacije na prethodnom stupnju utječe na izračune naknadnih faza kako bi se postigao najbolji rezultat općenito. Dinamičko programiranje takvo načelo odlučivanja naziva metodom optimalnosti, koja određuje da optimalna strategija za rješavanje problema, bez obzira na početne odluke i uvjete, mora biti optimalna strategija za početno stanje u kasnijim fazama. Kao što vidimo, proces rješavanja problema je kontinuirana optimizacija rezultata u svakom odvojenom stupnju od prvog do posljednjeg. Ova metoda se naziva metoda gornjeg programiranja. Slika shematski prikazuje algoritam rješenja od vrha do dna. Ali postoji jedna klasa višestepenih problema u kojoj je maksimalni učinak već poznat u posljednjoj fazi, na primjer, već smo stigli iz točke A u točku B i sada želimo znati jesmo li ispravno koračali u svakoj prethodnoj fazi ili ako bismo mogli učiniti nešto optimalnije. Pojavljuje se rekurzivni slijed faza, tj. Idemo kao da je "od suprotnog". Ova metoda rješavanja naziva se "metoda donjeg programiranja".

Praktična primjena

Dinamičko programiranje se može koristiti u bilo kojem područje djelovanja gdje postoje procesi koji mogu biti na bilo kojem parametru (vrijeme, količina, temperatura, itd.) podijeljeni u nekoliko identičnih malih faza. Najčešće korištene dinamičke metode rješavanja dobivene su u teoriji upravljanja i razvoju računalnih sustava.

Potražite najbolji put

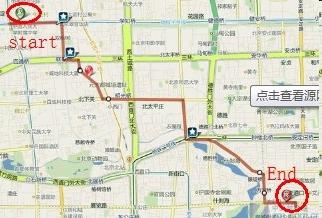
Pomoću dinamičke optimizacije moguće je riješiti široku klasu problema pronalaženja ili optimizacije najkraćeg puta i drugih problema u kojima „klasična“ metoda nabrajanja mogućih rješenja dovodi do povećanja vremena izračunavanja, a ponekad je općenito neprihvatljivo. Klasičan problem dinamičkog programiranja je problem ruksaka: dan je određeni broj objekata s određenom masom i cijenom, te je potrebno odabrati skup objekata s maksimalnom vrijednošću i masom koja ne prelazi volumen ruksaka. Klasično nabrajanje svih opcija u potrazi za optimalnim rješenjem trajat će dosta vremena, a uz pomoć dinamičkih metoda problem se rješava u razumnom vremenu. Zadaci pronalaženja najkraćeg puta za transportnu logistiku su osnovni, a dinamičke metode rješavanja optimalno su prikladne za njihovo rješavanje. Najjednostavniji primjer takvog zadatka je izgradnja najkraćeg puta automobilskim GPS navigatorom.

proizvodnja

Dinamičko programiranje široko se koristi u rješavanju različitih proizvodnih zadataka, kao što je upravljanje zalihama kako bi se u svakom trenutku održao potreban broj komponenti, zakazivanje proizvodnog procesa, održavanje opreme i remont, ujednačeno opterećenje osoblja, najučinkovitija raspodjela investicijskih fondova, itd. Za rješavanje proizvodnih problema korištenjem metoda dinamičkog programiranja razvijeni su posebni softverski paketi i. T Integriran je u popularne sustave upravljanja poduzećima kao što je SAP.

Znanstveno područje

Metode dinamičkog programiranja široko se koriste u različitim znanstvenim istraživanjima. Primjerice, uspješno se koriste u algoritmima za prepoznavanje govora i slika, u obradi velikih polja podataka u sociologiji i gospodarske aktivnosti.