Ostrogradsky - Gaussov teorem i formula

MV Ostrogradsky - ruski matematičar i fizičar od Ruskog carstva, akademik. On je dao ogroman doprinos razvoju matematička analiza teorija vjerojatnosti, mehanika (dio fizike) teorija brojeva. Godine 1826. izvukao je formulu, koja se sada naziva Ostrogradsky-Gaussova formula.

Povijest otkrića

Formulu Ostrogradsky-Gauss prvi je put spomenuo Joseph Lagrange 1762. godine.

Nadalje, glavnu metodu reduciranja trostrukog integrala na površinu dokazao je Karl Gauss, koji je kao temelj za dokaz koristio rješavanje problema u elektrodinamici. To se dogodilo u prvoj polovici XIX stoljeća.

Nadalje, formula u općem obliku predstavio je Mihail Ostrogradski. Uz njegovu pomoć, postalo je moguće izraziti vrijednost razlike u parametru iz N-puta integrala.

Značenje formule Ostrogradsky

Ostrogradsky-Gaussova formula povezuje trostruki integralni iznad prostornog volumena s integralom na površini na licu. To je analog Greenove formule, koja povezuje dvostruki integralni dio iznad ravnine s krivocrtnom duž njenih granica.

Izvođenje formule

Ostrogradsky - Gaussova formula: zaključak. Pretpostavimo da je u domeni W definirana integrandska funkcija R (x, y, z) koja je definirana i kontinuirana. Njegov derivat je sličan u cijeloj domeni W, uključujući i njezinu granicu. U ovom obliku, sada je poznat Ostrogradsky - Gaussov teorem (formula je dana dolje).

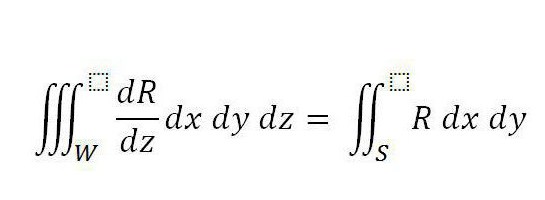
Štoviše, S je površina koja graniči tijelo, a integralni dio desno je raspoređen na njegovu vanjsku stranu.

I apsolutno istinito

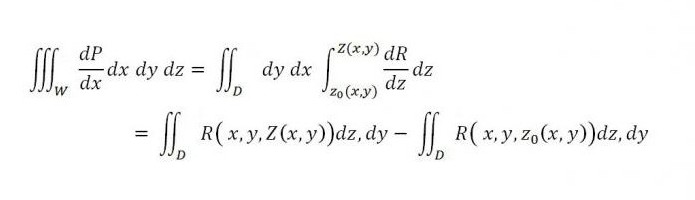
Ako na sličan način uzmemo u obzir integrale na površini, onda

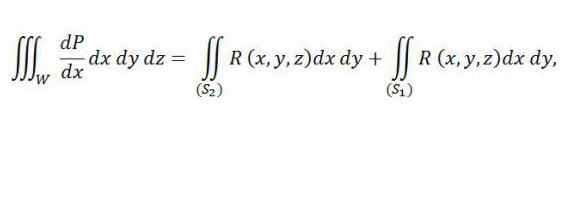
dok je na desnoj strani zbroj dvaju integrala - prvi je povezan s gornjim dijelom površine (S2), a drugi s donjim dijelom površine (S ₁ ). Ako ovoj jednakosti na desnoj strani dodamo sljedeći integralni sastojak, njegova valjanost neće biti povrijeđena:

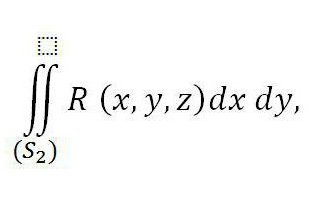
Ona odgovara vanjskom dijelu površine S3 zbog jednakosti nuli.

Ako kombiniramo sva tri gorenavedena integrala u jedan, dobit ćemo poseban slučaj Ostrogradske formule.

Lako je shvatiti da je ova formula istinita za širu klasu tijela i vrijedi i za figure koje su ograničene apsolutno svim nelinearnim površinama.

Slijedeće formule su slične:

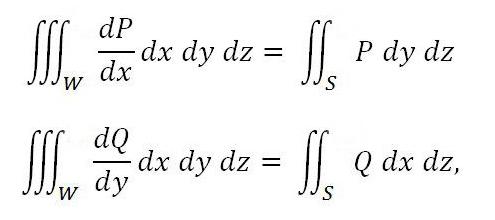
ako su funkcije Q i P kontinuirane u domeni zajedno s njihovim derivatima dP / dx i dQ / dy.

Ako dodamo obje jednakosti, dobivamo izraz za Ostrogradsku formulu. Prikazuje integral preko površine, povezan s vanjskim dijelom površine, preko trostrukog integrala, koji je preuzet od samog tijela, čija je granica gore spomenuta površina.

Treba razumjeti da formule Zelena, Stokesa i Ostrogradskog izražavaju integral koji je povezan s određenim geometrijskim tijelom, kroz integral koji se uzima na njegovoj granici. Greenova formula se koristi samo u slučaju dvodimenzionalnosti prostora, Stokesova formula se primjenjuje na zakrivljeni dvodimenzionalni prostor.

Newton-Leibnizova formula također se može smatrati nekim analogom ovih formula, ali za jednodimenzionalni prostor.

Korištenje ove formule

Neka kontinuirane funkcije A, B i C budu dane u bilo kojoj neotvorenoj regiji prostora, a uzimajući u obzir bilo koju zatvorenu površinu koja je u određenom području i graniči neko tijelo, možemo uzeti u obzir sljedeći integralni dio po površini:

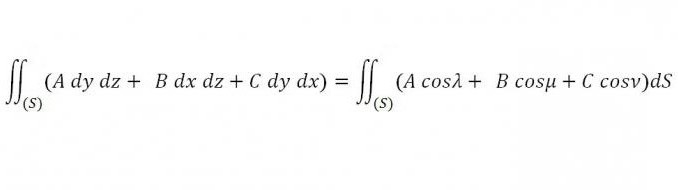
Potrebno je pronaći takve vrijednosti A, B i C, tako da je za svaki x, y i z ovaj integral jednak nuli.

Da biste to učinili, upotrijebite formulu Ostrogradsky-Gauss. Jedan od pretpostavljenih uvjeta je sigurnost i kontinuitet funkcija A, B i C i njihovih izvedenica.

Također je potrebno posebno uvesti najviše zadano ograničenje za određeni slučaj: i tijelo i površina koje ga omeđuju moraju biti istovremeno sadržani u određenom i specificiranom području, nazvanom jednostavno spojenom. Njegova glavna značajka je odsustvo praznog prostora (uključujući i prostor točaka). Dakle, granica tijela bit će jedna i s tim jedna površina.

Nakon primjene formule, moguće je dobiti sljedeći uvjet, koji je dovoljan:

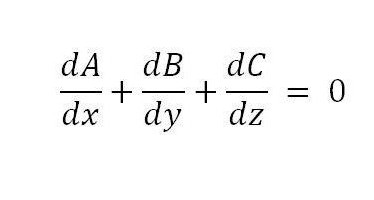
Da bi se dokazalo da je uvjet također nužan, dovoljno je koristiti diferencijaciju trostrukog integrala.

U zaključku, potrebno je reći o područjima uporabe.

Kako se u praksi koristi formula Ostrogradsky-Gauss? Primjeri upotrebe mogu se naći na raznim poljima: izvesti neke formule u fizici (npr. Difuzijska jednadžba), transformirati integrale, izračunati Gaussove integrale, dokazati neke formule i još mnogo toga.