Paralelnost ravnina: znak, stanje

Svatko tko je ikada studirao ili trenutno studira u školi morao se suočiti s različitim poteškoćama u proučavanju disciplina koje su uključene u program koji je razvilo Ministarstvo obrazovanja.

S kojim se teškoćama treba suočiti

Učenje jezika popraćeno je pamćenjem postojećih gramatičkih pravila i glavnim izuzecima od njih. Tjelesni odgoj zahtijeva mnogo izračuna, fizičke kondicije i velikog strpljenja od učenika.

Međutim, nemoguće je usporediti s poteškoćama koje se javljaju pri proučavanju točnih disciplina. Algebra koja sadrži zamršene načine rješavanja elementarnih problema. Fizika s bogatim nizom formula fizikalnih zakona. Geometrija i njezini dijelovi, koji se temelje na složenim teoremima i aksiomima.

Primjer bi mogli biti aksiomi koji objašnjavaju teoriju paralelnosti ravnina, koja se nužno mora zapamtiti, budući da leže u cijelom tijeku školskog kurikuluma u stereometriji. Pokušajmo shvatiti kako se to lakše i brže može učiniti.

Paralelne ravnine primjerima

Aksiom, koji ukazuje na paralelnost ravnina, glasi: " Svaka dva ravnina smatra se paralelnim samo ako ne sadrže zajedničke točke ", tj. Ne sijeku se međusobno. Da bismo zamislili ovu sliku detaljnije, kao elementarni primjer, možemo dati omjer stropa i poda ili suprotnih zidova u zgradi. Odmah postaje jasno što se podrazumijeva, a također potvrđuje činjenicu da se u uobičajenom slučaju te ravni nikada neće presjeći.

Drugi primjer je prozorska staklena jedinica, gdje staklene mreže djeluju kao ravnine. Oni ni pod kojim uvjetima neće formirati točke presijecanja. Osim toga, možete dodati police za knjige, Rubikovu kocku, gdje su ravnine njegove suprotne strane, i druge elemente svakodnevnog života.

Zadebljene ravnine označene su posebnim znakom u obliku dvije ravne crte "||", koje jasno ilustriraju paralelnost ravnina. Dakle, primjenjujući stvarne primjere, može se stvoriti jasnija percepcija teme i, prema tome, može se nastaviti dalje prema razmatranju složenijih pojmova.

Gdje i kako se primjenjuje teorija paralelnih ravnina?

Studenti geometrije u školi se suočavaju s mnogostranim problemima, gdje je često potrebno odrediti paralelnost linija, linija i ravnina između njih ili ovisnost ravnina jedna od druge. Analizirajući postojeće stanje, svaki zadatak može biti povezan s četiri glavne klase stereometrije.

Prva klasa uključuje zadatke u kojima je potrebno odrediti paralelnost linije i ravnine među sobom. Njegovo rješenje svodi se na dokazivanje teorema istog naziva. Da bi se to postiglo, potrebno je odrediti postoji li paralelna ravna linija koja leži u toj ravnini za pravac koji ne pripada dotičnoj ravnini.

Druga klasa zadataka uključuje one u kojima je uključeno obilježje paralelizma ravnina. Koristi se za pojednostavljenje procesa dokazivanja, čime se značajno skraćuje vrijeme pronalaženja rješenja.

Sljedeća klasa pokriva raspon problema usklađenosti s izravnim osnovnim svojstvima paralelizma ravnina. Rješenje problema četvrtog razreda sastoji se u utvrđivanju je li zadovoljen uvjet paralelizma ravnina. Znajući točno kako se dokazuje određeni problem, učenicima postaje lakše upravljati svojim postojećim arsenalom geometrijskih aksioma.

Dakle, zadaci, čije stanje zahtijeva definiranje i dokazivanje paralelnosti ravnih linija, ravne linije i ravnine ili dviju ravnina između njih, svodi se na ispravan odabir teorema i rješenja prema postojećem skupu pravila.

O paralelizmu linije i ravnine

Paralelizam ravne linije i ravnine posebna je tema u stereometriji, budući da je to temeljni koncept na kojem se temelje sva sljedeća svojstva paralelizma geometrijskih figura.

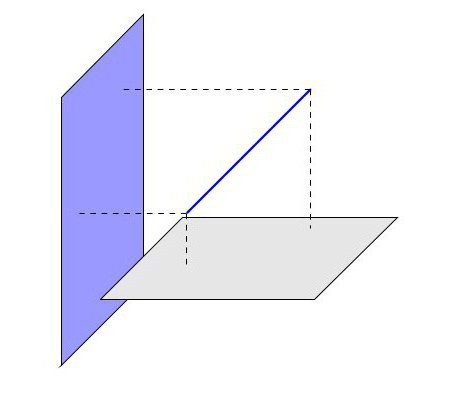
Prema postojećim aksiomima, u slučaju kada dvije točke ravne crte pripadaju određenoj ravnini, možemo zaključiti da u njoj leži i ta ravna crta. U ovoj situaciji postaje jasno da postoje tri opcije za položaj ravne linije u odnosu na ravninu u prostoru:

1. Linija pripada zrakoplovu.
2. Za ravnu liniju i ravninu postoji jedna zajednička točka presijecanja.
3. Za pravac i ravninu odsutne su točke presjeka.

Posebno smo zainteresirani za potonju opciju, kada nema točaka presijecanja. Tek tada možemo reći da su pravac i ravnina međusobno paralelni. Dakle, potvrđuje se uvjet glavnog teorema o paralelnom znaku ravne linije i ravnine, koji kaže da: "Ako je pravac koji ne pripada dotičnoj ravnini paralelan bilo kojoj pravoj na toj ravnini, onda je i pravac paralelan s danom ravninom".

Potreba da se koristi obilježje paralelizma

Znak paralelnosti ravnina, u pravilu, koristi se za traženje pojednostavljenog rješenja problema o ravninama. Suština ove značajke je sljedeća: " Ako postoje dvije ravne linije koje se međusobno sijeku, koje leže u jednoj ravnini, paralelne s dvije ravne crte koje pripadaju drugoj ravnini, tada se takve ravnine mogu nazvati paralelne ."

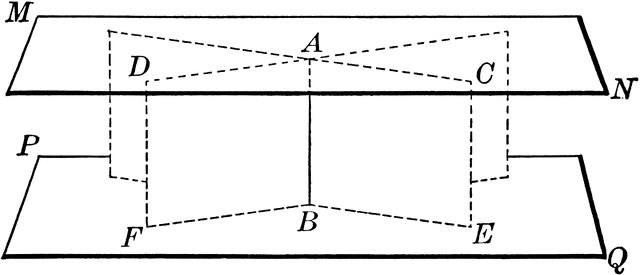
Dodatni teoremi

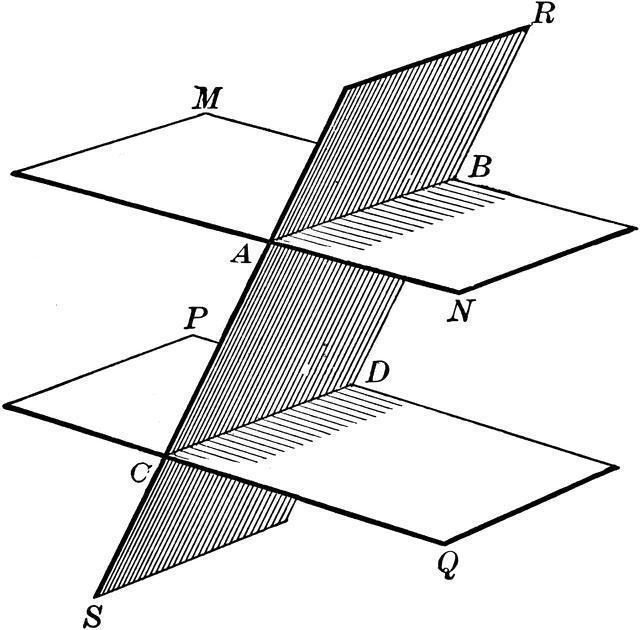
Osim uporabe znaka koji dokazuje paralelnost ravnina, u praksi se možete susresti s upotrebom još dva dodatna teorema. Prvi je prikazan u sljedećem obliku: " Ako je jedna od dviju paralelnih ravnina paralelna s trećom, onda je druga ravnina paralelna s trećom ili potpuno s njom ".

Na temelju uporabe reducibilnih teorema, uvijek se može dokazati paralelnost ravnina s obzirom na razmotreni prostor. Drugi teorem pokazuje ovisnost ravnina o okomitoj pravoj liniji i izgleda ovako: " Ako su dvije neusklađene ravnine okomite u odnosu na neku ravnu crtu, tada se one smatraju paralelnim jedna s drugom ".

Pojam nužnih i dostatnih uvjeta

Pri rješavanju problema dokazivanja paralelizma ravnina nekoliko puta izveden je nužan i dovoljan uvjet za paralelnost ravnina. Poznato je da se svaka ravnina daje parametarskom jednadžbom oblika: A ₁ x + B ₁ y + C ₁ z + D ₁ = 0. Naše se stanje temelji na korištenju sustava jednadžbi koje definiraju raspored ravnina u prostoru i prikazano je sljedećim riječima: " Da bismo dokazali paralelnost dviju ravnina, nužno je i dostatno da sustav jednadžbi koje opisuju te ravnine nije kompatibilan, tj. Nema rješenja ."

Osnovna svojstva

Međutim, pri rješavanju geometrijskih problema, korištenje obilježja paralelizma nije uvijek dovoljno. Ponekad se dogodi situacija kada je potrebno dokazati paralelnost dviju ili više linija u različitim ravninama ili jednakost segmenata zatvorenih na tim linijama. Da biste to učinili, primijenite svojstva paralelnih ravnina. U geometriji postoje samo dva.

Prvo svojstvo omogućuje nam da prosudimo paralelnost linija u određenim ravninama i prikazujemo u sljedećem obliku: " Ako dvije paralelne ravnine sijeku treću, onda će linije koje tvore linije presjeka također biti paralelne jedna drugoj ."

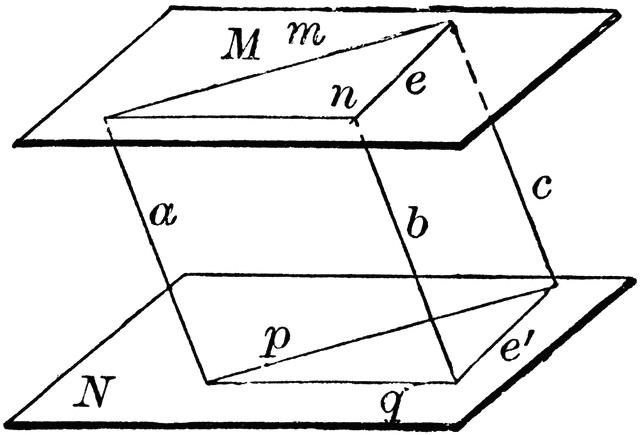
Značenje drugog svojstva je dokazati jednakost segmenata smještenih na paralelnim ravnim linijama. Njegova interpretacija je prikazana u nastavku. " Ako razmotrimo dvije paralelne ravnine i zatvorimo regiju između njih, onda se može tvrditi da će duljina segmenata koje tvori ova regija biti ista ."