Svojstva i formule pravokutne prizme

Prizma je jedna od savršenih volumetrijskih figura, zajedno s loptom, cilindrom i piramidom, o čijim se osobinama raspravlja u posebnom dijelu geometrije - stereometrije. U ovom članku raspravljamo o glavnim karakteristikama pravokutne prizme.

Brojka prizme

Mnogi ljudi znaju za trokutaste prizme ili šesterokutne prizme, ali ne i svaka osoba ima jasnu predodžbu o tome što je ta brojka uopće. U geometriji, pod njim se razumije prostorni objekt koji je omeđen s dva identična poligona i nekoliko četverokuta. Dva poligona nazivaju se prizma baze. Oni leže u paralelnim ravninama. Svi četverokuti su paralelogrami i tvore bočnu površinu slike.

Glavne formule i svojstva prizme tiču ​​se pitanja određivanja volumena, površine njegove površine i broja elemenata koji tvore lik. Sastav potonjeg uključuje vrhove, rubove i lica. Količine tih elemenata međusobno su povezane Eulerovim izrazom za poliedre. Ima sljedeći oblik:

Broj rubova = broj lica + broj vrhova - 2

Budući da je bočna površina prizme uvijek predstavljena paralelogramima, njezine glavne značajke ovise o tipu poligona koji leži u temeljima te slike. Ako je poligon trokut, onda se prizma naziva trokutasta, ako je četverokut četverokutan i tako dalje.

Pravokutna prizma

Ako je kut između svake strane prizme i njegove baze 90 ^° , tada se takva figura naziva pravokutna. Napominjemo da govorimo o kutu između stranica, a ne između rebara. Često se takva figura naziva izravnom prizmom.

Kada je označeni kut 90 ^o , svi paralelogrami automatski postaju pravokutnici. To je još jedan razlog zašto se ova prizma naziva pravokutnom. Donja slika pokazuje kako izgleda pravokutna prizma.

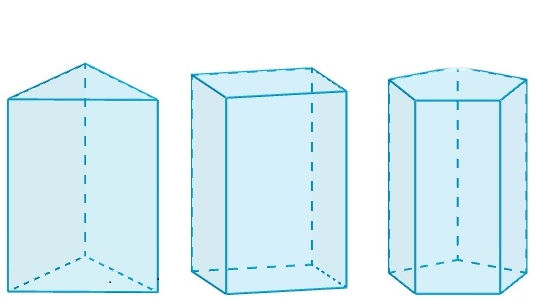
Ovdje vidimo da se svaka od tri prizme razlikuje od ostalih po tipu poligona na kojem se nalazi oblik. Na slici su prikazane trokutaste, četverokutne i peterokutne prizme. Broj pravokutnika za svaku od njih je 3, 4, odnosno 5.

Važno svojstvo pravokutne prizme, koja ga razlikuje od kosog kuta, jest činjenica da se dužina njegovog bočnog ruba podudara s visinom slike. Ovo svojstvo je vrlo pogodno za izračunavanje njegove površine i volumena.

Ispravna prizma

Svaka izravna prizma na kojoj leži pravilan poligon naziva se regularna. Navedeni poligon mora imati istu duljinu svih strana i jednake kutove. Takav pravokutnik je jednakostraničan trokut, kvadrat, pentagon i tako dalje.

Na donjoj slici prikazane su dvije prizme. Lijevo je točno, jer u bazi je kvadrat i ravan. Desna, unatoč činjenici da je linija ravna, nije ispravna, budući da je njezina baza proizvoljni četverokut.

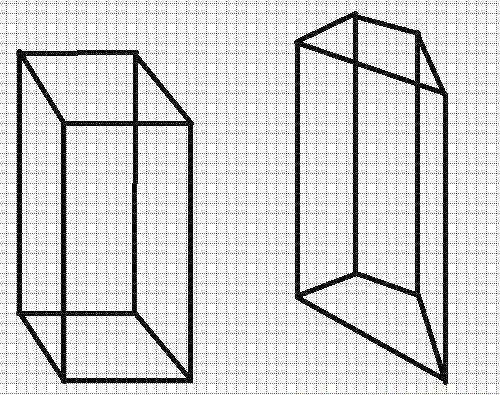
Jedina ispravna prizma koja ima svoje ime je kocka. Dobiva se kada se visina slike podudara s duljinom stranice kvadrata u podnožju.

Budući da je područje za pravilan poligon lako izračunati, tada je za svaku regularnu prizmu poznate formule za njegovu površinu i volumen.

Područje pravilnog poligona

Prije davanja formula za površinu i volumen pravokutne prizme, razmotrite pravilan poligon.

Donja slika prikazuje skup regularnih poligona, osim kruga.

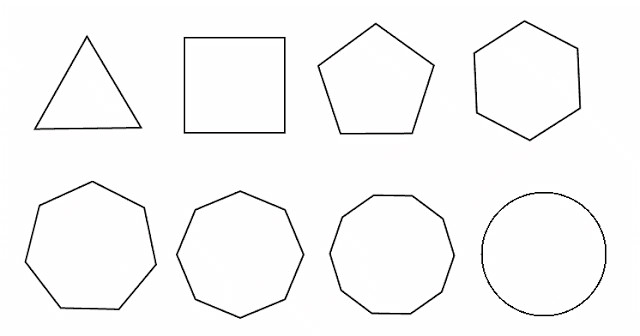
Vidljivo je da se za svaku od njih broj strana podudara s brojem uglova. Štoviše, sve strane i kutovi su isti. Ta nam svojstva omogućuju da damo formulu koja je univerzalna za sve pravilne poligone i omogućuje nam da izračunamo njihovo područje. Formula ima oblik:

S _n = n / 4 * a ² * ctg (pi / n)

Gdje je a dužina stranice, n je broj strana (vrhova) oblika. Simbol ctg označava kotangentnu trigonometrijsku funkciju.

Pokazujemo kako se koristi ovaj izraz. Na primjer, izračunajmo područje jednakostraničnog trokuta. Za njega n = 3, tada:

S ₃ = 3/4 * a ² * ctg (pi / 3) = 3/4 * a ² * 1 / =3 = √ 3/4 * a ²

Sada upotrijebite ovu formulu za kvadrat. Imamo:

S ₄ = 4/4 * a ² * ctg (pi / 4) = a ² * 1 = a ²

To jest, dobili smo poznati izraz za trg kvadrata.

Površina prizme

Kada je dana geometrijska definicija dotične figure, pokazalo se da se sastoji od dvije baze i više paralelograma. Taj je broj točno jednak broju strana poligona u bazi. Površina razmatrane figure može se zapisati sljedećom formulom:

S = 2 * S _o + S _b

Gdje je S _o - osnovna površina, S _b - bočna površina. Budući da se potonji sastoji od n paralelograma, njegova je vrijednost jednaka zbroju njihovih područja.

U slučaju pravilne ravne prizme, bočna će površina biti formirana pravokutnicima sa stranama a i h, gdje je a dužina osnovne strane, h je visina prizme. Za slučaj n pravilnog kvadrata dobivamo formulu za područje S _tot prizme:

S _tot = n / 2 * a ² * ctg (pi / n) + n * a * h

Na donjoj slici prikazano je skeniranje šesterokutne prizme.

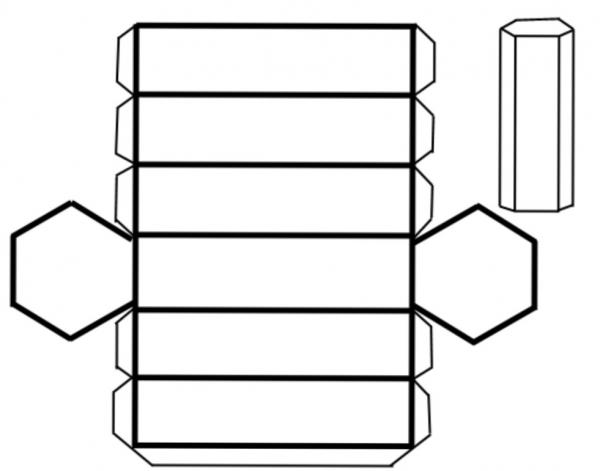
Može se vidjeti da je lik oblikovan s dva pravilna šesterokuta i šest jednakih pravokutnika, čija je jedna strana jednaka strani šesterokuta. Primjenom gornjeg izraza za ovu prizmu dobivamo:

S ⁶ _tot = _6/2 * a ² * ctg (pi / 6) + 6 * a * h = 3 * a * (*3 * a + 2 * h)

Formula za volumen

Volumen prizme se općenito izračunava pomoću sljedeće jednostavne formule:

V = S _o * h

Za pravokutni oblik, visina je njezin rub, tako da se ovaj izraz lako primjenjuje. Primjerice, izračunavamo volumen za trokutastu pravilnu prizmu. Površina njegove baze već je izračunata, jednaka je:

S ₃ = /3 / 4 * a ²

Tada će vrijednost volumena oblika biti sljedeća:

V = S3 * h = /3 / 4 * a ² * h

Formule za ravnu prizmu s pravilnim poligonom na dnu pokazuju da se sva svojstva za takve brojke mogu dobiti ako poznajete samo dva parametra: duljinu stranice n-kuta i visinu prizme.