Visina piramide: definicija, formule, kalkulacije

Jedna od volumetrijskih veličina proučavanih tijekom prostorne geometrije je piramida. Važna značajka ove brojke je njegova visina. U članku ćemo dati definiciju visine piramide i dati formule preko kojih je povezana s drugim linearnim karakteristikama.

Što je piramida

Pod piramidom razumijemo geometrijski oblik prostornog, koji se dobiva spajanjem svih kutova poligona s jednom točkom u prostoru. Donja slika prikazuje raspored linija (rubova) za četverokutne i peterokutne piramide.

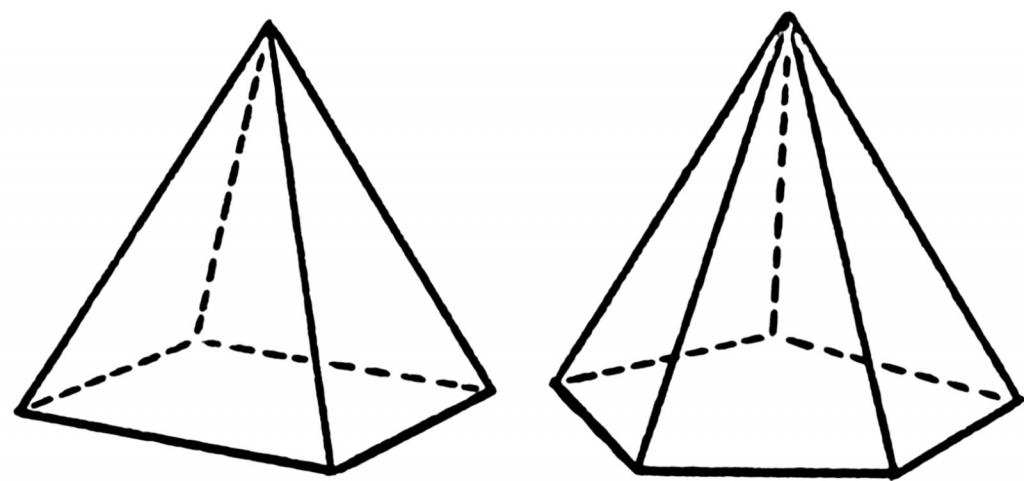
Poligonalno lice oblika naziva se njegova baza. Točka gdje se sva trokutasta lica spajaju zove se vrh. Za određivanje visine piramide važni su označeni elementi.

Visina tijela

Visina piramide naziva se okomica, koja se od vrha spušta na ravninu baze. Važno je razumjeti da se iz svakog vrha koji pripada osnovici figure također može nacrtati okomica na odgovarajuće trokutasto lice, ali neće se pojaviti kao visoka. Visina piramide je jedina okomita koja je jedna od važnih linearnih značajki.

Svaka učenica zna da svaka ravna figura posjeduje geometrijski centar (u fizici odgovara središtu mase). Primjerice, geometrijsko središte proizvoljnog trokuta određeno je točkom sjecišta njezinih srednjih točaka, za paralelogram, točku sjecišta dijagonala. Ako visina piramide presijeca svoju bazu u geometrijskom središtu, tada se ta brojka naziva ravnom linijom. Piramida je ravna, s osnovnim poligonom s istim stranama i kutovima, koji se naziva točnim.

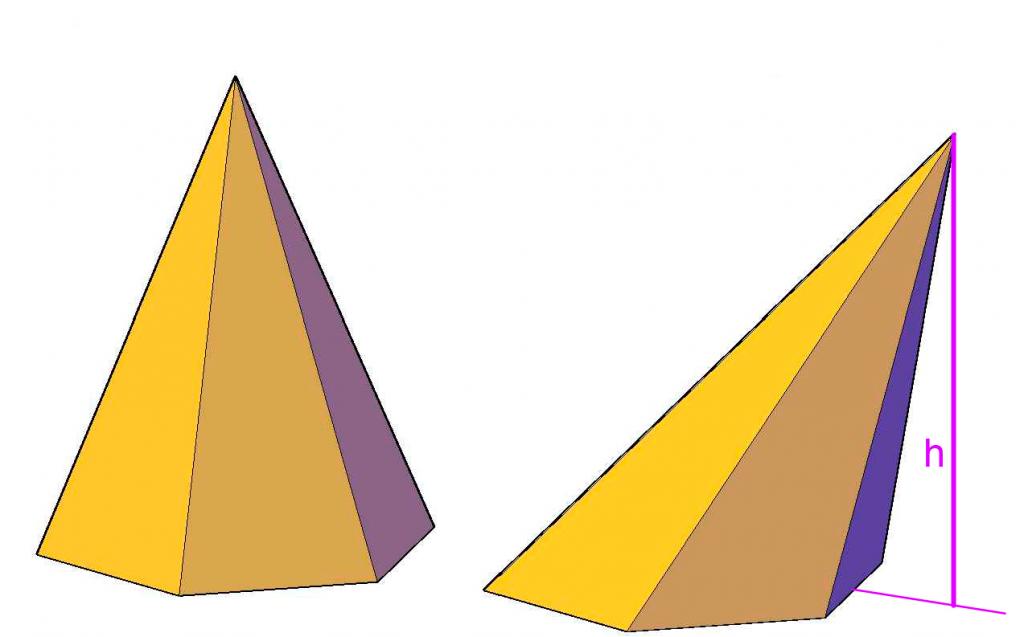
Gornja slika pokazuje razliku između pogrešne i ispravne piramide. Može se vidjeti da visina nepravilnog oblika leži izvan njezine osnove, dok je u pravilnoj šesterokutnoj piramidi visina unutar oblika, presjecajući svoju bazu u geometrijskom središtu.

Važna svojstva svih regularnih piramida su sljedeća:

• sve bočne strane su jednakokrake trokute i jednake su jedna drugoj;
• duljine bočnih rebara i apotema su iste.

Formule za visinu pravilne piramide

Postoje četiri osnovne linearne karakteristike za bilo koju točnu piramidu:

• strana baze;
• bočni rub;
• apotemom bočne strane;
• visina slike.

Sve su matematički međusobno povezane. Duljinu stranice baze označimo a, visinom - h, apothem - h _b i rubom - b. Formule koje vežu te količine imaju individualni izgled za odgovarajuću piramidu n-ugljena. Na primjer, za pravilnu piramidu, četverokutna visina može se odrediti pomoću formula:

h = √ (a _b2 - a 2/4);

h = √ (b ² - a 2/2).

Te formule proizlaze iz Pitagorina teorema kada se razmatraju odgovarajući pravokutni trokuti unutar piramide.

Ako se uzme u obzir figura s trokutastom bazom, sljedeće vrijednosti vrijede za visinu regularne piramide:

h = √ (a _b ² - a 2/12);

h = √ (b ² - a 2/3).

Rješenje problema sa šesterokutnom piramidom

Pretpostavimo da smo dobili pravilnu piramidu s heksagonalnom bazom. Poznato je da je visina podnožja piramide 13 cm, s obzirom da je dužina bočnog ruba 10 cm, potrebno je izračunati volumen i visinu pravilne šesterokutne piramide.

Donja slika pokazuje kako izgleda pravi šesterokut.

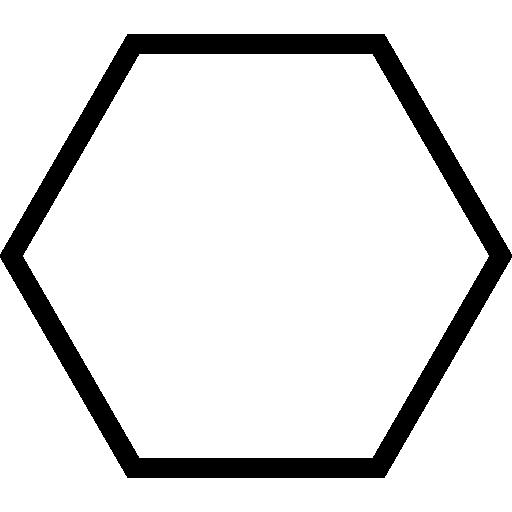
Udaljenost između bilo koje njezine dvije paralelne strane naziva se visina. Nije teško pokazati da je ta visina h _a povezana s duljinom stranice slike sa sljedećom formulom:

h _a = a *. 3

Zamjenjujući vrijednost izraza h _a nalazimo da je osnovna strana a jednaka 7,51 cm.

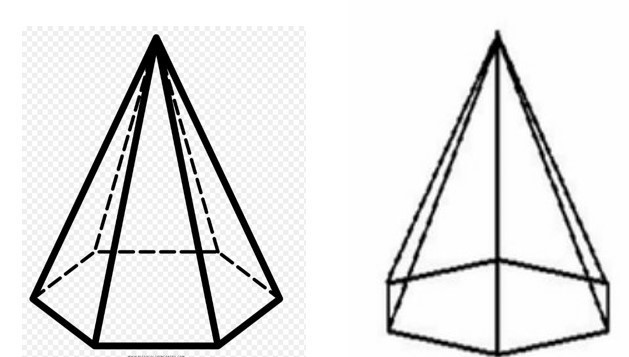
Visinu h slike možemo odrediti ako razmotrimo pravokutni trokut unutar piramide i koji se sastoji od dvije noge (visina piramide i polovica dijagonale šesterokutne baze) i hipotenuza (bočni rub). Tada će vrijednost h biti jednaka:

h = √ (b ² - a ² ) = √ (100 - 56,4) = 6,6 cm.

Volumen piramide definira se kao treći dio produkta visine figure na području njezine baze. Područje pravilnog šesterokuta je:

S6 = n / 4 * a ² * ctg (pi / n) = 6/4 * a ² * ctg (pi / 6) = 3 * / ² 3/2 * a ² = 3 * / ² 3/2 * 56, 4 ≈ 146,53 cm2.

Formula koja se koristi za izračunavanje S6 je univerzalna za proizvoljni regularni n-gon.

Za određivanje volumena slike ostaje zamjena parametara koji se nalaze u odgovarajućoj formuli:

V = 1/3 * h * S6 = 1/3 * 6.6 * 146.53 = 322.366 cm3.

Dobili smo vrijednost visine piramide i izračunali njen volumen. Dakle, problem je riješen.