Zakon loma svjetlosti: formulacija i praktična primjena

Fenomen loma svjetlosnog vala shvaća se kao promjena smjera širenja fronte ovog vala pri prelasku iz jednog prozirnog medija u drugi. Mnogi optički instrumenti i ljudsko oko koriste ovaj fenomen za obavljanje svojih funkcija. U članku se razmatraju zakoni loma svjetlosti i njihova primjena u optičkim uređajima.

Procesi refleksije i loma svjetlosti

S obzirom na pitanje zakona loma svjetlosti, potrebno je spomenuti fenomen refleksije, budući da je usko povezan s tom pojavom. Kada svjetlo prolazi iz jednog prozirnog medija u drugi, tada se na sučelju tih medija istovremeno odvijaju dva procesa:

1. Dio svjetlosnog snopa reflektira se natrag prema prvom mediju pod kutom koji je jednak kutu upada početne grede na granici.
2. Drugi dio grede ulazi u drugo okruženje i nastavlja se širiti u njemu.

Gore navedeno pokazuje da će intenzitet početnog svjetlosnog snopa uvijek biti veći od intenziteta reflektiranog i lomljenog svjetla odvojeno. Kako je taj intenzitet raspodijeljen između greda ovisi o svojstvu medija i kutu upadanja svjetla na granici.

U čemu je bit procesa loma svjetlosti?

Dio snopa svjetlosti koji pada na površinu između dva prozirna medija nastavlja se širiti u drugom mediju, ali će se smjer njegovog širenja već razlikovati od izvornog smjera u 1. mediju pod određenim kutom. To je fenomen loma svjetlosti. Fizički uzrok ovog fenomena je razlika u brzini širenja svjetlosnog vala u različitim okruženjima.

Podsjetimo se da svjetlost ima maksimalnu brzinu širenja u vakuumu, jednaka je 299,792,458 m / s. U bilo kojem materijalu, ova brzina je uvijek niža, a što je gustoća medija veća, to se elektromagnetski val širi u njemu. Na primjer, u zraku, brzina svjetlosti je 299,705,543 m / s, u vodi pri 20 ° C već 224,844,349 m / s, au dijamantu ona pada više od 2 puta u odnosu na brzinu u vakuumu, te je 124,034,943 m / s.

Huygensovo načelo

Ovaj princip osigurava geometrijsku metodu za pronalaženje fronte vala u bilo koje vrijeme. Princip Huygensa pretpostavlja da je svaka točka do koje valna linija doseže izvor elektromagnetskih sekundarnih valova. Šire se u svim smjerovima istom brzinom i frekvencijom. Dobiveni valni val definira se kao skup frontova svih sekundarnih valova. Drugim riječima, fronta je površina koja dodiruje sfere svih sekundarnih valova.

Prikaz primjene ovog geometrijskog načela za određivanje valne fronte prikazan je na donjoj slici. Kao što se može vidjeti iz ove sheme, svi radijusi sfera sekundarnih valova (prikazani strelicama) su isti, budući da se prednji val širi u homogenom mediju s optičkog gledišta.

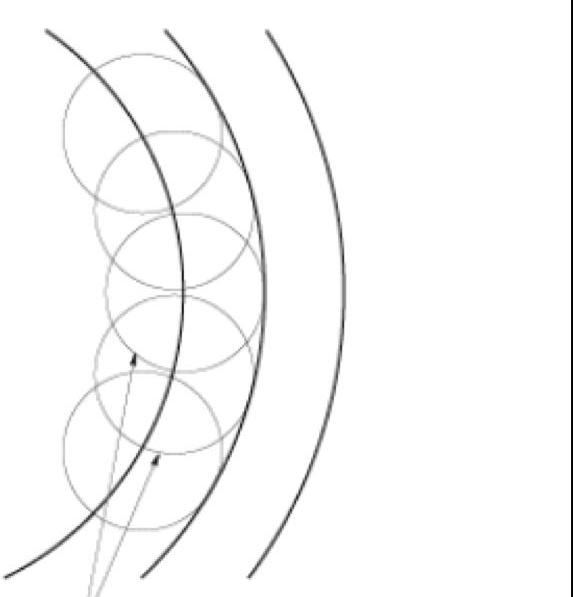
Primjena načela Huygensa na proces loma svjetlosti

Da bismo razumjeli zakon loma svjetlosti u fizici, možemo koristiti načelo Huygensa. Razmotrimo neki svjetlosni tok koji pada na sučelje između dva medija, a brzina kretanja elektromagnetskog vala u prvom mediju je veća od one za drugu.

Čim dio prednje strane (s lijeve strane na slici ispod) dođe do odvajanja medija, na svakoj točki površine sučelja počinju se pobuđivati ​​sekundarni sferni valovi, koji će se već širiti u drugom mediju. Budući da je brzina svjetlosti u drugom mediju manja od ove vrijednosti za prvi medij, dio fronte koji još nije dosegnuo granicu između medija (desno na slici) nastavit će se širiti većom brzinom od onog dijela fronte (lijevo) koji je već pao u drugu okolinu , Crtanje krugova sekundarnih valova za svaku točku s odgovarajućim radijusom jednako v * t, gdje je t određeno specifično vrijeme širenja sekundarnog vala, i v je brzina njegovog širenja u drugom mediju, a zatim crtanje tangentne krivulje na sve površine sekundarnih valova, možete dobiti prednji širenje svjetla u drugom okruženju.

Kao što se može vidjeti na slici, ovaj će se prednji dio otkloniti pod nekim kutom od početnog smjera njegovog širenja.

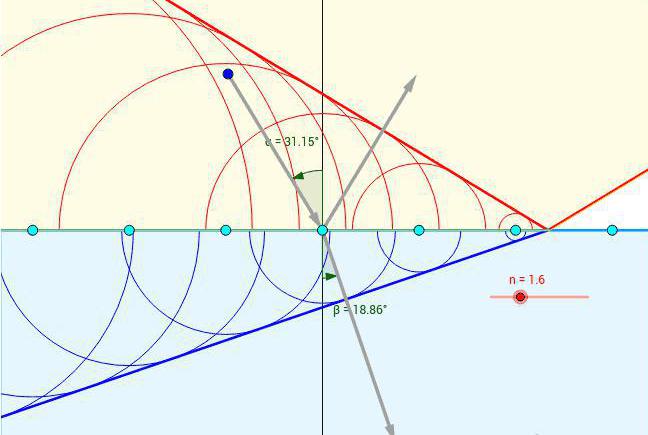
Treba primijetiti da ako su brzine vala jednake u oba medija, ili ako je svjetlo palo okomito na granicu, onda ne bi moglo biti govora o refrakcijskom procesu.

Zakoni loma svjetlosti

Ti su zakoni dobiveni eksperimentalno. Neka su 1 i 2 dva prozirna medija, a brzine širenja elektromagnetskih valova su v ₁ i v ₂ . Neka snop svjetlosti padne na granici od medija 1 pod kutom θ ₁ do normale, au drugom mediju se nastavlja širiti pod kutom θ ₂ u odnosu na normalu sučelja. Tada će formulacija zakona loma svjetlosti biti kako slijedi:

1. U istoj ravnini bit će dvije grede (upadne i lomljene) i norma vraćena na međusklop između medija 1 i 2.
2. Omjer brzina širenja snopa u mediju 1 i 2 bit će izravno proporcionalan omjeru sinusa kutova upada i loma, tj. Sin (θ ₁ ) / sin (θ ₂ ) = v ₁ / v ₂ .

Drugi zakon se zove Snellov zakon. Ako uzmemo u obzir da se indeks ili indeks loma prozirnog medija definira kao odnos brzine svjetlosti u vakuumu prema toj brzini u mediju, tada se formula za zakon loma svjetlosti može ponovno napisati kao: sin (θ ₁ ) / sin (θ ₂ ) = n ₂ / n ₁ , gdje su n1 i n2 indeksi loma medija 1 i 2, redom.

Dakle, matematička formula zakona pokazuje da je proizvod sinusa kuta i indeks loma za određeni medij konstantna vrijednost. Štoviše, uzimajući u obzir trigonometrijska svojstva sinusa, možemo reći da ako v ₁ > v ₂ , svjetlo će se pomaknuti bliže normalnom prilikom prolaska kroz sučelje i obrnuto.

Kratka povijest otkrića zakona

Tko je otkrio zakon loma svjetlosti? Zapravo, prvi put ju je formulirao srednjovjekovni astrolog i filozof Ibn Sahl u 10. stoljeću. Sekundarno otkriće zakona dogodilo se u 17. stoljeću, a to je učinio nizozemski astronom i matematičar Snell van Royen, tako da drugi svjetski zakon loma ima njegovo ime.

Zanimljivo je primijetiti da je malo kasnije ovaj zakon otvorio i Francuz Rene Descartes, stoga u zemljama francuskog govornog područja nosi svoje ime.

Primjer zadatka

Svi problemi zakona loma svjetlosti temelje se na matematičkoj formulaciji Snellovog zakona. Navedimo primjer takvog zadatka: potrebno je za vrijeme prijelaza iz dijamanta u vodu pronaći kut razmnožavanja fronte svjetlosti, pod uvjetom da to prednje strane padne na sučelje pod kutom od 30 ^o u odnosu na normalu.

Da bi se riješio ovaj problem, potrebno je poznavati ili refrakcijske indekse razmatranog medija ili brzinu širenja elektromagnetskog vala u njima. Pozivajući se na referentne podatke, možemo zapisati: n ₁ = 2.417 i n ₂ = 1.333, gdje brojevi 1 i 2 označavaju dijamant i vodu.

Zamjenjujući dobivene vrijednosti u formulu, dobivamo: sin (30 ^o ) / sin (θ ₂ ) = 1,333 / 2,417 ili sin (θ ₂ ) = 0,39 i θ ₂ = 65,04 ^o , tj. Snop će se značajno ukloniti iz normale.

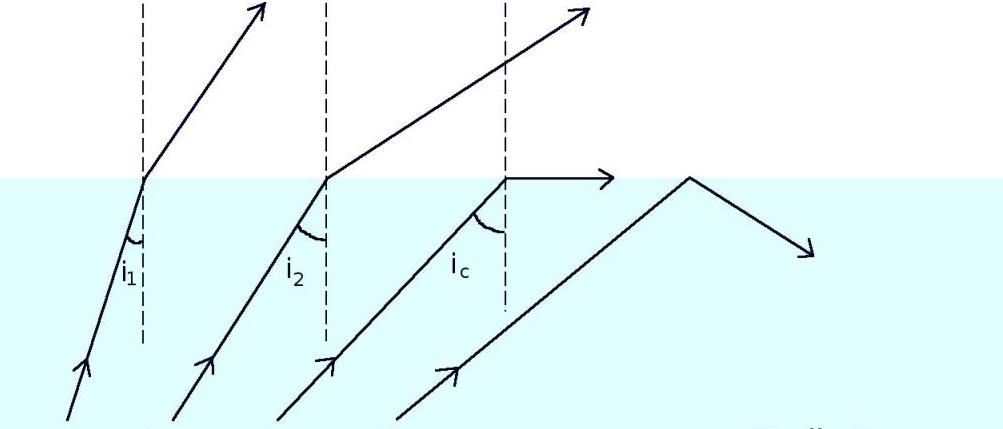
Zanimljivo je primijetiti da, ako je kut upadanja bio veći od 33,5 ^o , tada, u skladu s formulom zakona loma svjetlosti, ne bi postojao refrakcijski zrak, a cijeli bi se dio svjetlosti reflektirao natrag u dijamantni medij. Ovaj je učinak u fizici poznat kao potpuno unutarnje refleksija.

Gdje se primjenjuje zakon loma?

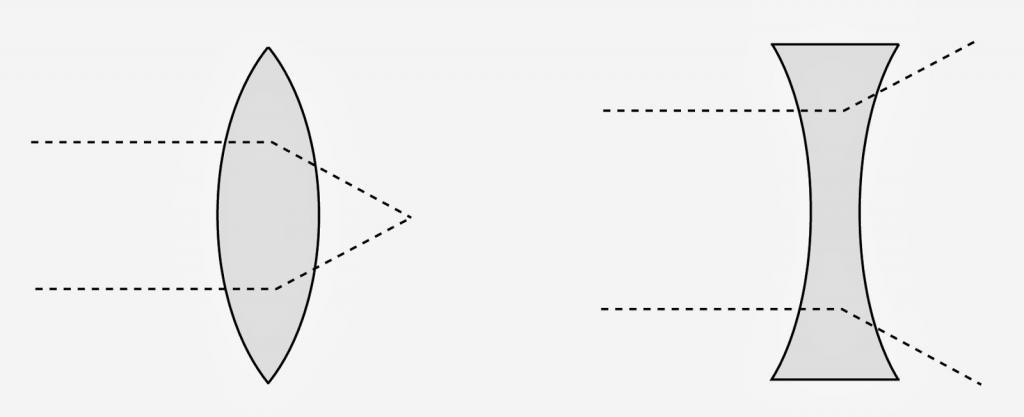
Praktična primjena zakona loma svjetlosti je raznolika. Može se bez pretjerivanja reći da većina optičkih uređaja radi na ovom zakonu. Refrakcija svjetlosnog toka u optičkim lećama koristi se u uređajima kao što su mikroskopi, teleskopi i dalekozori. Bez postojanja refraktivnog učinka, bilo bi nemoguće da osoba vidi svijet oko sebe, jer su staklasto tijelo i leće oka biološke leće koje obavljaju funkciju fokusiranja svjetlosnog toka na točku na osjetljivoj mrežnici oka. Osim toga, zakon potpune unutarnje refleksije nalazi svoju primjenu u svjetlosnim vlaknima.