Projekcija točke na ravnini. Projekcija točke na ravnoj liniji na ravnini
Proučavanje svojstava figura u prostoru i na ravnini je nemoguće bez poznavanja udaljenosti između točke i takvih geometrijskih objekata kao što su pravac i ravnina. U ovom članku ćemo pokazati kako pronaći te udaljenosti, uzimajući u obzir projekciju točke na ravnini i na ravnoj liniji.
Jednadžba pravca za dvodimenzionalne i trodimenzionalne prostore
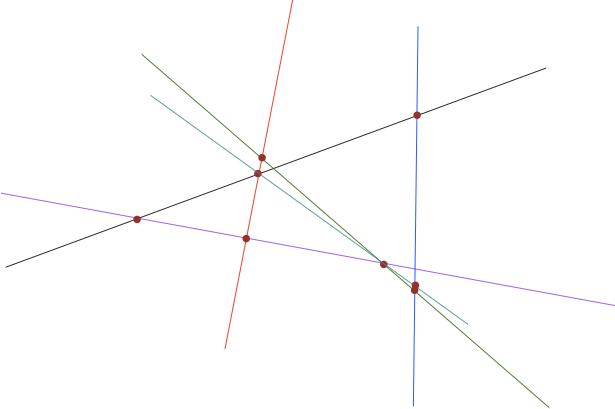
Izračunavanje udaljenosti točke do ravne linije i ravnine provodi se pomoću njegove projekcije na te objekte. Da bi se pronašle te projekcije, treba znati u kojem obliku su dane jednadžbe za ravne linije i ravnine. Počnimo s prvim.
Ravna crta je skup točaka, od kojih se svaka može dobiti iz prethodnog prijenosom u paralelne vektore. Primjerice, postoji točka M i N. Vektor MN them koji ih povezuje uzima M do N. Postoji i treća točka P. Ako je vektor MP¯ ili NP¯ paralelan s MN¯, sve tri točke na jednoj liniji leže i formiraju ga.
Ovisno o dimenziji prostora, jednadžba koja definira pravac može promijeniti svoj oblik. Dakle, dobro poznata linearna ovisnost y koordinate o x u prostoru opisuje ravninu koja je paralelna s trećom z osi. S tim u vezi, u ovom ćemo članku razmotriti samo vektorsku jednadžbu za tu liniju. Ima isti izgled za ravninu i trodimenzionalni prostor.
U prostoru, pravac se može definirati sljedećim izrazom:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Ovdje koordinatne vrijednosti s nultim indeksima odgovaraju ravnoj liniji određene točke, u¯ (a; b; c) koordinate usmjeravajućeg vektora koji leži na danoj pravoj liniji, α je proizvoljni stvarni broj koji mijenja sve točke ravne linije. Ta se jednadžba naziva vektor.
Često se gornja jednadžba piše u otvorenom obliku:
x = x 0 + a * a;
y = y 0 + α * b;
z = z 0 + α * c
Slično tome, možemo napisati jednadžbu za ravnu liniju u ravnini, tj. U dvodimenzionalnom prostoru:
(x; y) = (x 0 ; y 0 ) + α * (a; b);
x = x 0 + a * a;
y = y 0 + α * b
Planska jednadžba
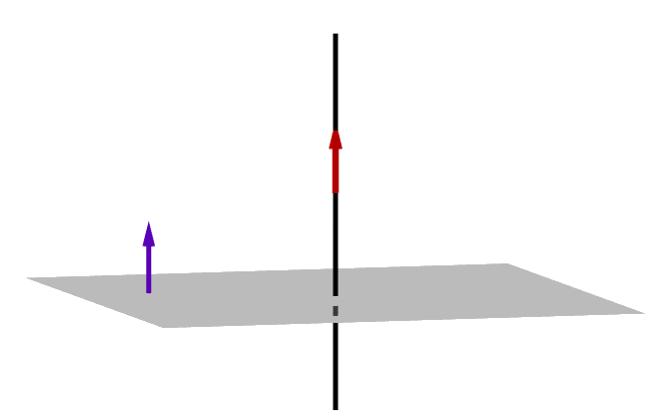
Da biste mogli pronaći udaljenost od točke do ravnina projekcija, morate znati kako je ravnina definirana. Kao i pravac, može se prikazati na nekoliko načina. Ovdje razmatramo samo jedno: opću jednadžbu.
Pretpostavimo da točka M (x 0 ; y 0 ; z 0 ) pripada ravnini, a vektor n ¯ (A; B; C) je okomit na nju, tada će za sve točke (x; y; z) ravnine biti slijedeća jednakost:
A * x + B * y + C * z + D = 0, gdje je D = -1 * (A * x 0 + B * y 0 + C * z 0 )
Treba imati na umu da su u ovoj općoj jednadžbi ravnine koeficijenti A, B i C koordinate normale ravnini vektora.
Izračun udaljenosti pomoću koordinata
Prije prelaska na razmatranje projekcija na ravnini točke i na pravoj liniji, treba podsjetiti kako treba izračunati udaljenost između dvije poznate točke.
Pretpostavimo da postoje dvije prostorne točke:
A 1 (x 1 ; y 1 ; z 1 ) i A 2 (x 2 ; y 2 ; z 2 )
Tada se udaljenost između njih izračunava po formuli:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2 )
Pomoću tog izraza određuje se i duljina vektora A 1 A 2 ¯.
Za slučaj na ravnini, kada su dane dvije točke sa samo jednim parom koordinata, možete napisati sličnu jednadžbu bez prisutnosti člana sa z u njemu:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 )
Sada razmotrimo različite slučajeve projekcije na ravnini točke na ravnoj liniji i na ravnini u prostoru.
Točka, linija i udaljenost između njih
Pretpostavimo da postoji neka točka i ravna crta:
P2 (xl; y1);
(x; y) = (x 0 ; y 0 ) + α * (a; b)
Udaljenost između tih geometrijskih objekata odgovara duljini vektora, čiji se početak nalazi u točki P 2 , a kraj je na takvoj točki P na označenoj pravoj, za koju je vektor P 2 P ¯ ove ravne linije okomit. Točka P naziva se projekcija točke P 2 na dotičnu liniju.
Na donjoj slici prikazana je točka P 2 , njezina udaljenost d do ravne crte, kao i vektor smjera v 1 ¯. Na liniji je odabrana i proizvoljna točka P 1, a iz nje se povlači vektor u P2. Točka P ovdje se podudara s mjestom gdje okomica presijeca crtu.
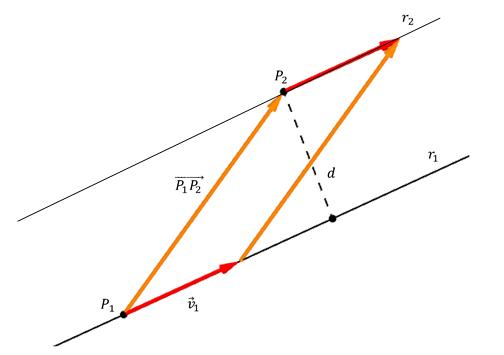
Vidljivo je da narančasta i crvena strelica tvore paralelogram, čije su strane vektor P 1 P 2 ¯ i v 1 ¯, a visina d. Iz geometrije je poznato da je za pronalaženje visine paralelograma njezino područje trebalo podijeliti s duljinom baze, na kojoj je spuštena okomica. Budući da je područje paralelograma izračunato kao vektorski proizvod njegovih strana, dobivamo formulu za izračunavanje d:
d = | [P 1 P 2 ¯ * v 1 ¯] | / | v 1 ¯ | |
Svi vektori i koordinate točaka u ovom izrazu su poznati, tako da ga možete koristiti bez ikakvih transformacija.
Taj bi se problem mogao riješiti drugačije. Da biste to učinili, zapišite dvije jednadžbe:
- skalarni proizvod P 2 P ¯ na v 1 ¯ treba biti jednak nuli, jer su ti vektori međusobno okomiti;
- koordinate točke P moraju zadovoljavati jednadžbu pravca.
Te su jednadžbe dovoljne za pronalaženje koordinata P, a zatim duljine d prema formuli iz prethodnog odlomka.
Zadatak pronalaženja udaljenosti između linije i točke
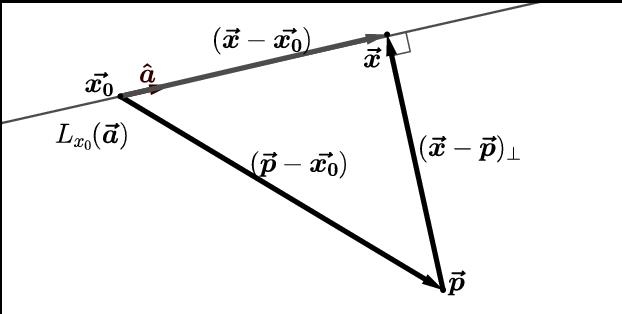
Pokazujemo kako te teorijske informacije koristiti za rješavanje određenog problema. Pretpostavimo da su poznata sljedeća točka i linija:
M (5; -3);
(x; y) = (3; 1) - α * (0; 2)
Potrebno je pronaći točke projekcije na ravnoj liniji na ravnini, kao i udaljenost od M do ravne crte.
Označiti projekciju koja se nalazi u točki M 1 (x 1 ; y 1 ). Taj problem rješavamo na dva načina, kako je opisano u prethodnom odlomku.
Metoda 1. Vektor smjera v 1 ¯ koordinate ima (0; 2). Za izradu paralelograma odaberite točku koja pripada pravoj liniji. Na primjer, točka s koordinatama (3; 1). Tada će vektor druge strane paralelograma imati koordinate:
(5; -3) - (3; 1) = (2; -4)
Sada je potrebno izračunati produkt vektora koji definiraju strane paralelograma:
[(2; -4) * (0; 2)] = 4
Zamjenimo ovu vrijednost u formulu, dobivamo udaljenost d od M do pravca:
d = 4 / =4 = 2
Metoda 2. Sada ćemo na drugi način pronaći ne samo udaljenost, nego i koordinate projekcije M na liniji, kako to zahtijeva uvjet problema. Kako je gore spomenuto, za rješavanje problema potrebno je stvoriti sustav jednadžbi. Izgledat će ovako:
(x 1 -5) * 0 + (y 1 +3) * 2 = 0;
(x 1 ; y 1 ) = (3; 1) -α * (0; 2)
Rješavamo ovaj sustav:
y1 = -3;
x 1 = 3
Projekcija početne točke koordinate je M1 (3; -3). Tada je potrebna udaljenost:
d = | MM 1 ¯ | = √ (4 + 0) = 2
Kao što možete vidjeti, oba rješenja dala su isti rezultat, što ukazuje na ispravnost izvedenih matematičkih operacija.
Projekcija točke na ravnini
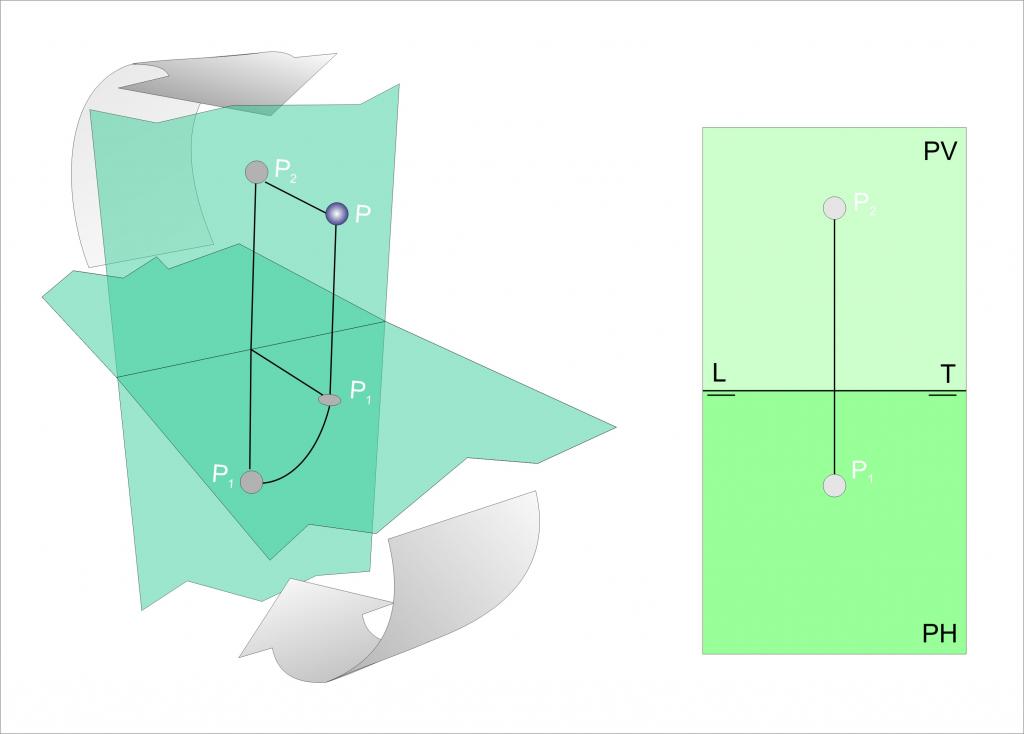
Sada razmislite što je projekcija točke dane u prostoru na određenoj ravnini. Lako se može pretpostaviti da je ova projekcija i točka, koja zajedno s izvornom oblikuje vektor okomit na ravninu.
Pretpostavimo da projekcija na ravninu koordinata točke M ima sljedeće:
M 1 (x 1 ; y 1 ; z 1 )
Sama ravnina opisana je jednadžbom:
A * x + B * y + C * z + D = 0
Na temelju tih podataka možemo napraviti jednadžbu prave linije koja prelazi ravninu pod pravim kutom i prolazi kroz M i M 1 :
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (A; B; C)
Ovdje su varijable s nultim indeksima koordinate točke M. Položaj na ravnini točke M 1 može se izračunati na temelju toga da njegove koordinate moraju zadovoljiti obje pisane jednadžbe. Ako ove jednadžbe nisu dovoljne za rješavanje problema, tada se može koristiti uvjet paralelizma MM 1 ¯ i vektor smjera za zadanu ravninu.
Očito, projekcija točke koja pripada ravnini podudara se sa samim sobom, a odgovarajuća udaljenost je nula.
Zadatak s točkom i ravninom
Neka je dano mjesto M (1; -1; 3) i ravnina koja je opisana sljedećom općom jednadžbom:
-x + 3 * y -2 * z + 4 = 0
Potrebno je izračunati koordinate projekcije na ravnini točke i izračunati udaljenost između tih geometrijskih objekata.
Za početak konstruiramo jednadžbu pravca koji prolazi kroz M i okomito na navedenu ravninu. Izgleda kao:
(x; y; z) = (1; -1; 3) + α * (- 1; 3; -2)
Označimo točku gdje ta ravna crta siječe ravninu, M1. Jednakosti za ravninu i ravnu liniju moraju biti zadovoljene ako zamjenimo M 1 koordinate u njima. Pišući izričito iz jednadžbe pravca, dobivamo sljedeće četiri jednadžbe:
-x 1 + 3 * y 1 -2 * z 1 + 4 = 0;
x 1 = 1 - a;
y1 = -1 + 3 * a;
z 1 = 3 - 2 x
Iz zadnje jednakosti dobivamo parametar α, zatim ga zamjenjujemo u pretposljednjem i drugom izrazu, dobivamo:
a = (3-z1) / 2;
y1 = -1 + 3 * (3-z 1 ) / 2 = -3 / 2 * z1 + 3.5;
x 1 = 1 - (3-z 1 ) / 2 = 1/2 * z 1 - 1/2
Izraz za y 1 i x 1 zamjenjuje se jednadžbom za ravninu, imamo:
-1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3.5) -2 * z 1 + 4 = 0
Gdje ćemo dobiti:
z 1 = 15/7
zatim:
y1 = -3 / 2 * 15/7 + 3.5 = 2/7;
x 1 = 1/2 * 15/7 - 1/2 = 4/7
Utvrdili smo da projekcija točke M na zadanu ravninu odgovara koordinatama (4/7; 2/7; 15/7).
Sada izračunajte udaljenost | MM 1 ¯ |. Koordinate odgovarajućeg vektora su:
MM 1 ¯ (-3/7; 9/7; -6/7)
Potrebna udaljenost je:
d = | MM 1 ¯ | = 6126/7 ≈ 1.6
Tri točke projekcije
Tijekom izrade crteža često je potrebno dobiti projekcije dijelova na međusobno okomite tri ravnine. Stoga je korisno uzeti u obzir što će projekcije određene točke M s koordinatama (x 0 ; y 0 ; z 0 ) na tri koordinatne ravnine biti jednake.

Nije teško pokazati da je xy ravnina opisana jednadžbom z = 0, xz ravnina odgovara izrazu y = 0, a preostala yz ravnina označena je jednakošću x = 0. Lako je pretpostaviti da će projekcije točke na 3 ravnine biti jednake:
za x = 0: (0; y 0 ; z 0 );
za y = 0: (x 0 ; 0; z 0 );
za z = 0: (x 0 ; y 0 ; 0)
Gdje je važno znati projekcije točke i njezinu udaljenost od ravnina?
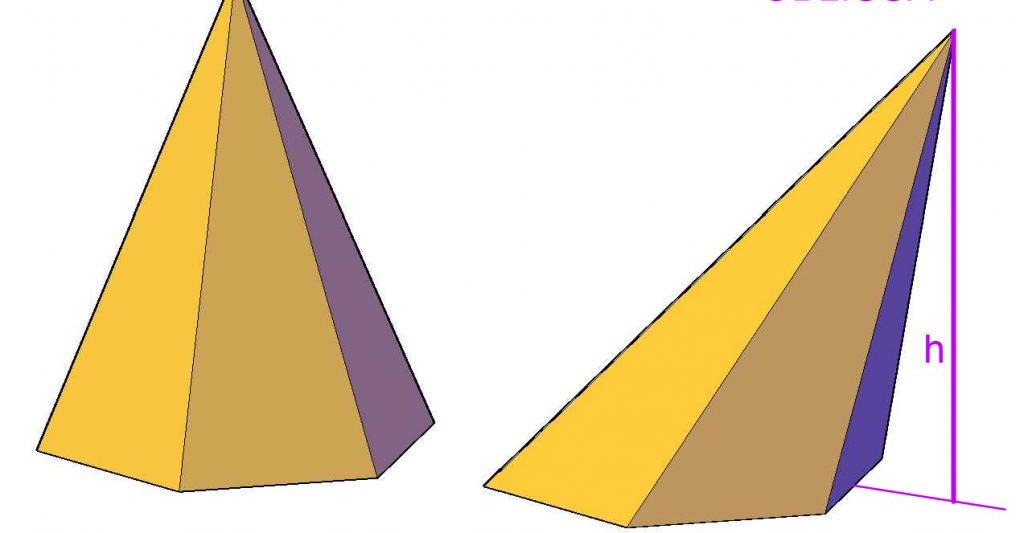
Određivanje položaja projekcije točaka na danoj ravnini važno je pri pronalaženju takvih veličina kao što su površina i volumen za kosu prizmu i piramidu. Na primjer, udaljenost od vrha piramide do ravnine baze je visina. Potonje je uključeno u formulu za volumen ove brojke.
Razmatrane formule i metode za određivanje projekcija i udaljenosti od točke do ravne linije i ravnine su prilično jednostavne. Važno je samo zapamtiti odgovarajuće oblike ravninskih i izravnih jednadžbi, ali i imati dobru prostornu imaginaciju kako bismo ih uspješno primijenili.