Turingov stroj: opis i primjeri Turingovih strojeva
Turingov stroj jedan je od najintrigantnijih i najzanimljivijih intelektualnih otkrića 20. stoljeća. Riječ je o jednostavnom i korisnom apstraktnom modelu računalstva (računalnom i digitalnom), što je prilično uobičajeno za realizaciju bilo kojeg računalnog zadatka. Zahvaljujući jednostavnom opisu i ponašanju matematička analiza ona čini temelj teorijske informatike. Ova je studija dovela do dubljeg znanja o digitalnim računalima i računici, uključujući i razumijevanje da postoje neki problemi u računanju koji se ne mogu riješiti na uobičajenim korisničkim računalima. 
Što je to i tko je stvorio
Alan Turing je pokušao opisati najprimitivniji model mehaničkog uređaja koji bi imao iste osnovne mogućnosti kao i računalo. Turing je prvi opisao automobil 1936. godine u članku "O izračunljivim brojevima s primjenom na problem rješivosti", koji se pojavio u Zborniku radova Matematičkog društva u Londonu. 
Turingov stroj je računalna naprava koja se sastoji od glave za čitanje / pisanje (ili "skener") s papirnom vrpcom koja prolazi kroz nju. Traka je podijeljena na kvadrate, od kojih svaka nosi jedan znak - "0" ili "1". Svrha mehanizma je da djeluje i kao sredstvo za ulazak i izlazak, i kao radna memorija za pohranjivanje rezultata međufaznih izračuna.
Od čega se uređaj sastoji
Svaki takav stroj sastoji se od dvije komponente:
- Neograničena vrpca. Beskonačan je u oba smjera i podijeljen je u stanice.
- Automatski kontrolirani program, skener glave za čitanje i pisanje podataka. Može biti u svakom trenutku u jednoj od mnogih država.
Svaki stroj spaja dvije konačne serije podataka: abecedu dolaznih simbola A = {a0, a1, ..., am} i abecedu stanja Q = {q0, q1, ..., qp}. Stanje q0 naziva se pasivno. Vjeruje se da uređaj završava svoj rad kada padne na njega. Stanje q1 naziva se početno - stroj započinje svoje kalkulacije, budući da je na početku u njemu. Ulazna riječ nalazi se na vrpci jedno slovo u nizu u svakom položaju. Na obje strane su samo prazne ćelije.
Kako mehanizam funkcionira
Turingov stroj ima temeljnu razliku od računalnih uređaja - njegov memorijski uređaj ima beskonačnu traku, dok za digitalne uređaje ovaj uređaj ima traku određene dužine. Svaka klasa zadataka rješava samo jedan izgrađen Turingov stroj. Ostale vrste zadataka uključuju pisanje novog algoritma.
Upravljački uređaj, koji je u jednom stanju, može se kretati u bilo kojem smjeru duž remena. Piše u stanice i čita od njih znakove konačne abecede. U procesu kretanja odabire se prazan element koji popunjava pozicije koje ne sadrže ulazne podatke. Algoritam za Turingov stroj određuje pravila prijelaza za upravljački uređaj. Oni postavljaju glavu za čitanje i pisanje na sljedeće parametre: upisivanje u ćeliju novog znaka, prebacivanje u novo stanje, pomicanje lijevo ili desno uz traku. 
Svojstva mehanizma
Turingov stroj, kao i drugi računalni sustavi, ima svoja svojstvena svojstva i sličan je svojstvima algoritama:
- Diskretna. Digitalni uređaj prelazi na sljedeći korak n + 1 tek nakon što je prethodni završen. Svaki završeni korak dodjeljuje ono što će biti n + 1.
- Razumljivost. Uređaj obavlja samo jednu radnju za istu ćeliju. Umeće znak iz abecede i čini jedan pokret: lijevo ili desno.
- Determinizam. Svaka pozicija u mehanizmu odgovara jednom ostvarenju specificirane sheme, a na svakom stupnju djelovanja i redoslijedu njihova izvođenja su nedvosmisleni.
- Učinkovitost. Točan rezultat za svaku fazu određuje Turingov stroj. Program izvršava algoritam iu konačnom broju koraka ulazi u stanje q0.
- Masačusets Svaki je uređaj definiran iznad valjanih riječi u abecedi.
Funkcije Turingova stroja
Rješenje algoritama često zahtijeva implementaciju funkcije. Ovisno o mogućnosti pisanja lanca za računanje, funkcija se naziva algoritamski rješivom ili nerješivom. Kao skup prirodnih ili racionalnih brojeva, riječi u konačnoj abecedi N za stroj, razmatra se niz skupa B - riječi unutar binarne kodne abecede B = {0.1}. Rezultat izračuna također uzima u obzir "nedefiniranu" vrijednost koja se javlja kada algoritam visi. Za provedbu funkcije važno je imati formalni jezik u konačnoj abecedi i rješivost problema prepoznavanja točnih opisa. 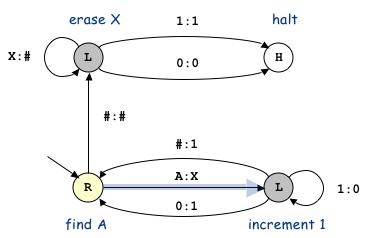
Program za uređaj
Programi za Turingov mehanizam formirani su tablicama u kojima prvi redak i stupac sadrže znakove vanjske abecede i vrijednosti mogućih unutarnjih stanja automata - unutarnje abecede. Tabelarni podaci su naredbe koje Turingov stroj percipira. Rješenje problema se javlja na ovaj način: slovo koje čita glava u ćeliji nad kojom se trenutno nalazi, i unutarnje stanje glave automata određuju koju naredbu treba izvršiti. Naime, takva se naredba nalazi na sjecištu simbola vanjske abecede i unutarnjeg, koji su u tablici. 
Komponente za izračune
Za izgradnju Turingovog stroja za rješavanje jednog specifičnog zadatka potrebno je odrediti sljedeće parametre.
Vanjska abeceda. To je neki konačni skup simbola, označen znakom A, čiji su sastavni elementi slova. Jedan od njih - a0 - mora biti prazan. Primjerice, abeceda Turingova uređaja koji radi s binarnim brojevima izgleda ovako: A = {0, 1, a0}.
Kontinuirani niz alfanumeričkih znakova zapisanih na traku naziva se riječ.
Automatski stroj je uređaj koji radi bez ljudske intervencije. U Turingovom stroju, on ima nekoliko različitih stanja za rješavanje problema i, pod određenim uvjetima, kreće se s jednog mjesta na drugo. Kombinacija takvih stanja vagona je unutarnja abeceda. Ima oznaku slova oblika Q = {q1, q2 ...}. Jedna od tih odredbi - q1 - trebala bi biti početna, tj. Ono što pokreće program. Drugi nužan element je stanje q0, koje je konačno, to jest, dovršava program i stavlja uređaj u položaj zaustavljanja.
Tablica konverzije. Ova komponenta je algoritam za ponašanje nosača uređaja, ovisno o trenutnom stanju stroja i vrijednosti simbola koji se čita. 
Algoritam za automat
Prijenos Turingovog uređaja tijekom rada kontrolira program, koji tijekom svakog koraka izvršava slijed sljedećih akcija:
- Pisanje vanjskog znaka abecede na mjesto, uključujući i prazan, zamjenom elementa koji je bio u njemu, uključujući i prazan.
- Pomaknite jedan korak ulijevo ili udesno.
- Promijenite svoje unutarnje stanje.
Dakle, prilikom pisanja programa za svaki par znakova ili pozicija, moraju se točno opisati tri parametra: i - element iz odabrane abecede A, smjer pomicanja nosača ("←" na lijevo, "→" na desno, "točka" - bez kretanja) i q k je novo stanje uređaja, na primjer, naredba 1 "←" q2 postavljena je na "zamjena znaka za 1, pomicanje glave nosača ulijevo pomoću jedne stupnjevite ćelije i provođenje prijelaza u stanje q 2 ".
Turingov stroj: primjeri
Primjer 1. Zadatak je izraditi algoritam koji dodaje jedan na posljednju znamenku danog broja koji se nalazi na vrpci. Ulazni podaci - riječ - znamenke cijelog decimalnog broja, zapisane u uzastopnim ćelijama na vrpci. U početku se uređaj nalazi nasuprot krajnjem desnom simbolu - znamenki broja.
Odluka. Ako je zadnja znamenka jednaka 9, mora se zamijeniti s 0, a zatim dodati jednom prethodnom znaku. Program u ovom slučaju za ovaj Turingov uređaj može biti napisan ovako:
| a 0 | 0 | 1 | 2 | 3 | ... | 7 | 8 | 9 | |
| q 1 | 1 H q 0 | 1 H q 0 | 2H q 0 | 3H q 0 | 4H q 0 | ... | 8 H q 0 | 9 H q 0 | 0 λ q 1 |
Ovdje q 1 je stanje promjene znamenke, q 0 je stajalište. Ako u q 1 automat fiksira element iz serije 0..8, onda ga zamjenjuje s jednim od 1..9, odnosno, a zatim se prebacuje u stanje q 0 , odnosno uređaj se zaustavlja. Ako nosač fiksira broj 9, zamjenjuje ga brojem 0, zatim se pomiče ulijevo, zaustavljajući se u stanju q 1 . Ovo kretanje se nastavlja sve dok uređaj ne fiksira znamenku manju od 9. Ako su svi znakovi jednaki 9, oni se zamjenjuju nulama, 0 zamjenjuje vodećim elementom, nosač će se pomaknuti ulijevo i upisati 1 u praznu ćeliju. Sljedeći korak će biti prijelaz u stanje q 0 - stop.
Primjer 2. S obzirom na niz znakova koji označavaju otvaranje i zatvaranje zagrada. Potrebno je izgraditi Turingov uređaj koji će ukloniti par recipročnih zagrada, to jest elemente poredane u red - "()". Na primjer, početni podaci: “) (() (()”, odgovor bi trebao biti: “) .. ((”. Rješenje: mehanizam, koji je u q 1 , analizira krajnji lijevi element u liniji.
| a 0 | ( | ) | |
| q 1 | a 0 H q 0 | (Pq2 | ) P q 1 |
| q2 | a 0 H q 0 | (Pq2 | ) λ q3 |
| q 3 | a 0 H q 0 | a 0 n q3 | a 0 n q1 |
Navedite q 1 : ako se pojavi simbol “(”), zatim pomaknite udesno i prijeđite na položaj q 2 ; ako je definirano “ 0 ”, zaustavite se.
Stanje q 2 : analiza zagrada “(” za prisutnost para provodi se, u slučaju slučajnosti treba ispasti “)”. Ako je element par, napravite kočnicu na lijevo i idite na q 3 .
Navedite q 3 : prvo izbrišite simbol “(”, a zatim “)” i idite na q 1 .