Što je ubrzanje? Vrste ubrzanja. Formula. Primjer rješavanja problema

Dio fizike odgovoran za proučavanje značajki gibanja u prostoru tijela naziva se kinematika. U ovom članku razmatramo koje se fizikalne veličine u kinematici koriste za opisivanje kretanja objekata, te također otkrivamo što je ubrzanje.

Fizičke veličine u kinematici

Kada se tijelo kreće u prostoru, važno je da znamo koju udaljenost putuje unutar određenog vremenskog razdoblja i po kojoj putanji se kreće.

Za opisivanje udaljenosti u fizici koristi se pojam putanje - L. U slučaju gibanja duž kruga, umjesto puta koristi se pojam rotacijskog kuta θ. Vrijednost L u SI mjeri se u metrima (m), a vrijednost θ mjeri se u radijanima (rad.).

Osim staze, važno je znati i brzinu kretanja tijela. Pod njim razumjeti brzinu prolaska udaljenosti. Matematički izraz za linearnu brzinu ima oblik:

v¯ = d L / dt

Za opisivanje kretanja u krugu primijenite kutnu brzinu ω koja se izračunava na sljedeći način:

ω¯ = d θ / dt

Treća važna količina kinematike je ubrzanje.

Što je ubrzanje? To je količina u fizici, koja pokazuje koliko brzo brzina varira tijekom vremena. Matematički se to može napisati kao:

a¯ = d v¯ / dt

Ako zamijenimo izraz za brzinu ovoj formuli ubrzanja, dobivamo:

a = d ² L / dt ²

Ubrzanje je prvi derivat brzine tijekom vremena ili drugi derivat tijekom vremena putovanja.

Tangencijalno i normalno ubrzanje

Iznad je dana definicija ubrzanja. Naziva se potpunim. U općem slučaju, smjer punog ubrzanja ne podudara se s smjerom vektora brzine. Potonja je tangenta na putanju kretanja na bilo kojoj od njezinih točaka.

Budući da je brzina vektorska veličina, mijenja se podrazumijeva sposobnost promjene modula i smjera. U prvom slučaju kažu da tijelo ima tangencijalno ubrzanje, u drugom je to normalno.

Formula za tangencijalno ubrzanje a _t se ne razlikuje od one za ubrzavanje pune a. Formula ima oblik:

a _t = dv / dt

To jest, tangencijalno, ili tangencijalno, kako se također naziva, ubrzanje se dobiva iz modula brzine tijekom vremena. Vektor a _t ¯ podudara se s vektorom v ¯ s ubrzanim kretanjem i suprotan je s usporenim pokretom.

Normalno ubrzanje je fizička veličina koja dovodi do zakrivljenosti pravocrtne putanje pokretnih tijela. Ona je usmjerena duž polumjera zakrivljenosti trajektorije, to jest normalno u odnosu na nju. Formula za njezinu definiciju je:

a _c = v2 / r

Normalno ubrzanje a _c ovisi o modulu brzine v i radijusu zakrivljenosti trajektorije r. Očito, u slučaju gibanja duž pravog radijusa, r se može smatrati jednakim beskonačnosti. Ovo posljednje znači da je normalno ubrzanje nula za pravocrtno gibanje.

Za kružna gibanja, vektor a _c ¯ usmjeren je na njegovo središte duž radijusa. Zbog toga se vrijednost _c također naziva centripetalno ubrzanje.

Puno ubrzanje

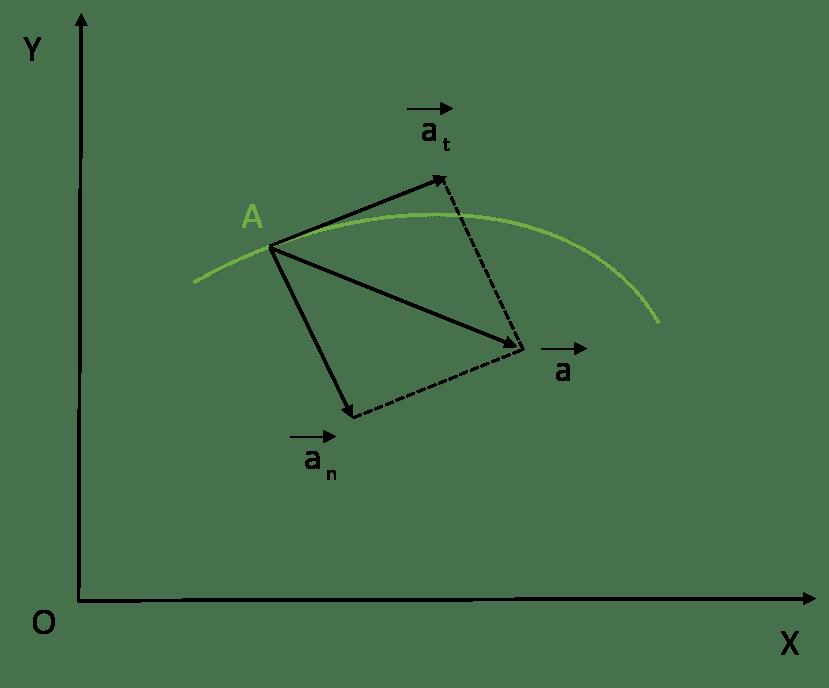
Vektor ukupnog ubrzanja je uvijek zbroj tangencijalnih i normalnih komponenti. Budući da su međusobno okomiti, Pitagorin teorem može se upotrijebiti za izračunavanje ukupnog modula ubrzanja. Željena formula za potpuno ubrzanje poprima oblik:

a = √ (a _t ² + a _c ² )

Da bi se odredilo gdje je vektor a¯ usmjeren, dovoljno je izračunati kut između njega i bilo koje komponente. Primjerice, kut the između vektora a i a _t jednak je:

ar = arctg (a _c / a _t )

Podsjetimo se da je centripetalno ubrzanje različito od nule samo kada je zakrivljenost putanje različita od beskonačnosti. U slučaju pravocrtnog gibanja, ukupno ubrzanje u magnitudi i smjeru jednako je tangencijalnoj komponenti.

Kutno ubrzanje

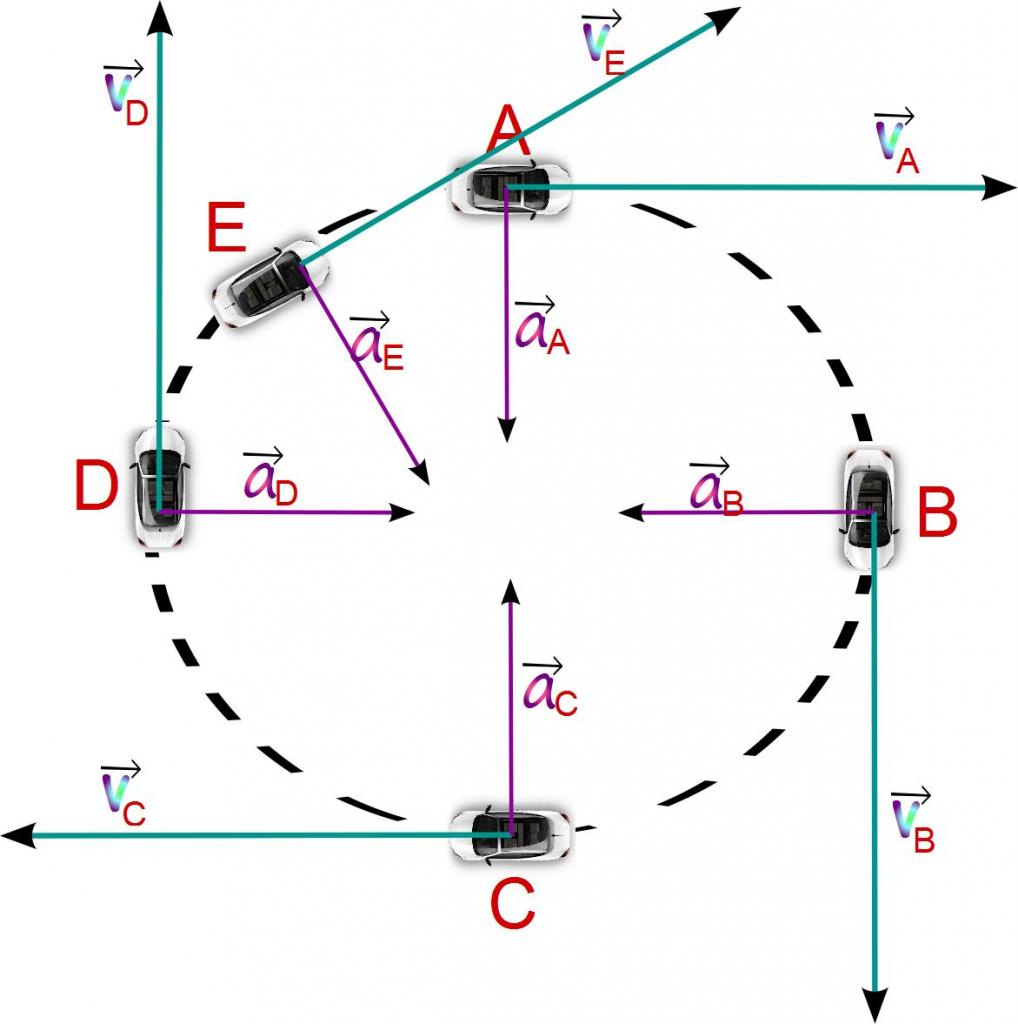
S obzirom na to da je takvo ubrzanje potrebno zadržati se na odgovarajućim kutnim karakteristikama.

Iznad je uveden koncept kutne brzine, koja se mjeri u radijanima u sekundi (rad / s). Ako nađemo derivaciju te brzine u odnosu na vrijeme, tada dobijemo veličinu kutnog ubrzanja:

α¯ = ω¯ / dt

Lako je pokazati da je kutna vrijednost povezana s tangencijalnom komponentom punog ubrzanja sljedećim odnosom:

a _t = α × r

Uz konstantno kutno ubrzanje, tangensna komponenta a _t će biti veća za točke koje su udaljenije od osi rotacije.

Kutno ubrzanje nema nikakve veze s normalnom komponentom.

Rješavanje problema određivanja ubrzanja

Pretpostavimo da se, krećući se s konstantom ubrzanja duž ravne linije, tijelo prevalilo na udaljenosti od 100 metara. Poznato je da je početna brzina tijela bila 1 m / s. Tijelo je prevalilo označenu udaljenost za 5,5 sekundi. Što je ubrzanje pokreta?

Prema stanju problema govorimo o ravnomjerno ubrzanom kretanju duž ravne putanje. Put koji se putuje u ovom slučaju može se izračunati pomoću formule:

L = v ₀ × t + a × t 2/2

Izražavajući iz jednakosti vrijednost a, imamo:

a = 2 × (L - v ₀ × t) / t ²

Sve vrijednosti na desnoj strani jednakosti poznate su iz stanja. Zamijenite ih i napišite odgovor: a = 6,25 m / s ² . Odnosno, tijekom svakog od 5,5 sekundi, brzina tijela se povećava za 6,25 m / s. Pronađena vrijednost ukupnog ubrzanja podudara se s tangencijalnom komponentom.