Što je egipatski sustav brojeva? Povijest, opis, primjeri

S nedostavnim egipatskim brojevnim sustavom, koji je korišten u starom Egiptu, vizualno smo upoznati s nekoliko preostalih papirusa. Primjeri zadataka i njihova rješenja toliko su zanimljivi u njima da ostaje samo žaliti što ih je tako malo.

Iz njih se može vidjeti da su matematika i egipatski brojevni sustav usko povezani s ekonomskim potrebama i praktičnom primjenom. Svake godine nakon poplave Nila bilo je potrebno obnoviti zgrade, preseliti zemljište, izračunati površinu i granice, voditi evidenciju o žetvi, kalendaru.

Što su pozicijski i nonpositional numerirani sustavi?

Odgovor leži u samom naslovu. Ako položaj znamenke utječe na rezultat izračuna, imamo pozicijski sustav brojeva, ako ne - ne pozicijski.

Ako napišemo 12, to je dvanaest, i sa istim brojevima, 21 je dvadeset i jedan. Prema egipatskom brojevnom sustavu: za pisanje 12, potrebno je dvaput upotrijebiti simbol jedinice, a simbol desetka i 21 izgledati kao jedan jedinstveni simbol i dva desetka simbola, to jest, samo trebate napisati tri simbola.

Nepozicijski su: rimski sustav, koji nam je poznat, u kojem su brojevi označeni rimskim slovima, slavenskim sustavom, gdje svako slovo također označava određeni broj ili broj. Rimski je sustav funkcionirao u zapadnoj Europi sve do 16. stoljeća.

Brojevni sustav koji koristimo u suvremenom životu je položajni decimalni sustav.

Nonpositional sustavi bili su vrlo pogodni za obavljanje jednostavnih aritmetičkih operacija, budući da su složeni izračuni uključivali glomazne zapise, koji nisu spriječili uspješan razvoj algebre i geometrije u starom Egiptu.

Kako su Egipćani mislili?

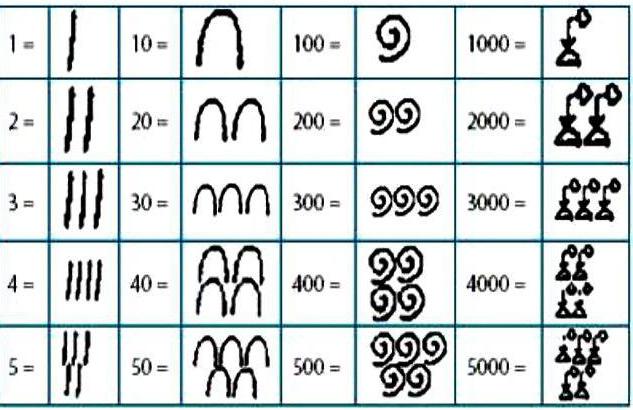
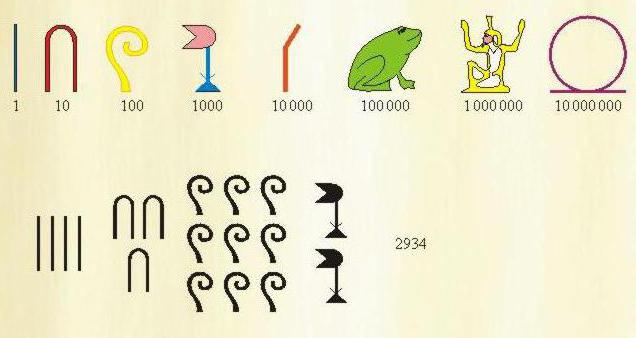
Što je to - egipatski sustav brojeva? Da bismo napisali bilo koji broj, koristili smo hijeroglife, označavajući određene brojeve, čiji je zbroj bio jednak željenoj vrijednosti.

Dostupne su posebne oznake za brojeve 1, 10, 100, 1000, 10000, 100000, 1000000. Prilikom upisivanja potrebnog broja, svaka oznaka je korištena do 9 puta. Zapisi u egipatskom brojevnom sustavu bili su u uzlaznom redu: prvo, jedinice, zatim desetke, stotine i tako dalje.

I pisali su, u pravilu, s desna na lijevo, ali bilo je moguće s lijeva na desno, iznos toga se nije promijenio. Također je korišteno i vertikalno pisanje, ali tada je odbrojavanje išlo od vrha prema dnu.

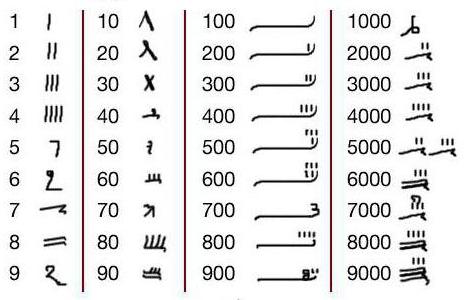
Upotrijebljena su dva načina pisanja:

1. Hijeroglif, u kojem su korišteni usvojeni hijeroglifi.
2. Hieratic, što je više shematski i praktično u praksi.

Povijesni obilazak

Povijest egipatskog brojevnog sustava nastala je u antičko doba, prvi rukopisi s brojevima odnose se na drugo tisućljeće prije Krista. Tada nije bilo novca, pa se sustav koristio i za nevjerojatnu složenost i veličinu matematičkih problema, kao i za rješavanje svakodnevnih svakodnevnih problema.

Naposljetku, poznavanje matematike korišteno je u geodetskim mjerenjima, u izradi kalendara i karata u astronomiji, plovidbi i izgradnji palača, kanala i vojnih utvrda.

Egipatski ne-pozicijski sustav brojeva korišten je sve do 10. stoljeća poslije Krista.

Imao je i mistično značenje, tajnu koju su svećenici nosili sa sobom, ali je djelomično otvorio svijet Pitagori. Ima djela u kojima opisuje simbolička značenja koja se daju digitalnim hijeroglifima, koje je napisao nakon boravka u Egiptu. Stoga njihov opis pripada egipatskom brojevnom sustavu.

Preživjelo je samo nekoliko papira s tim vremenima, čime se može razumjeti da je razina matematike visoka. Istinski je poznato da su Grci proučavali drevnu egipatsku matematiku. Jedno od najintimnijih znanja je egipatski ne-pozicijski sustav brojeva.

Papyrus Ahmes

Akhmes Papyrus datira iz 1650. godine prije Krista, sadrži 84 matematičkih zadataka. Pronađen je u Tebi, pohranjen u Britanskom muzeju.

Svi zadaci u papirusu razmatraju se na konkretnim primjerima egipatskog brojevnog sustava. Prikazuju primjere izračuna s razlomcima, s cijelim brojevima, dijeljenjem i množenjem.

Izračuni su dani za pronalaženje područja geometrijskih oblika: četverokut, krug, trokut.

Informacije iz papirusa dokazuju da su egipatski matematičari mogli izvaditi korijen, napraviti aritmetiku i geometrijska progresija jednadžbe s nepoznanicama.

Alikvotne frakcije

Zanimljivo je da su u izračunima korištene samo alikvotne frakcije, u kojima je brojnik bio jednak jednom i označen takvim znakom, a ispod njega su zapisane vrijednosti nazivnika, a sve ostale frakcije za izračune najprije je trebalo proširiti na alikvotne frakcije. No, oni su korišteni i imali su posebnu oznaku frakcije 2/3 i 3/4.

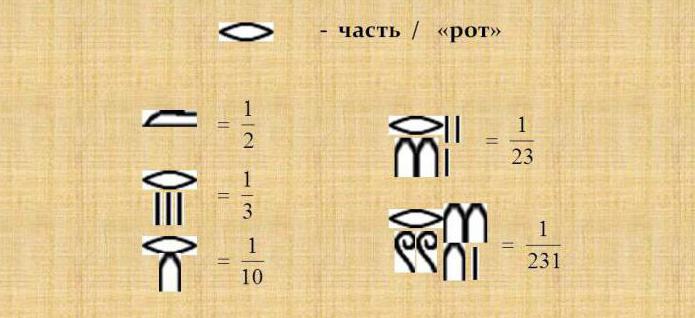
Da bi se uobičajene frakcije dovele u stanje alikvota na egipatski sustav brojeva, bilo je potrebno raditi:

4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2 + 1/4 + 1/20

2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28

3/7 = 12/28 = 24/56 = 14/56 + 7/56 + 3/56 = 1/4 + 1/8 + 1/18 + 1/56.

Frakcije su se formirale na moderan način: reduciranjem na zajednički nazivnik, za mnoge vrijednosti postojali su brojni gotovi stolovi.

množenje

Egipćani su naučili željeni rezultat, ne znajući tablicu množenja, ali koristeći znanje da ako se jedan faktor udvostruči i drugi faktor se smanji, rezultat se neće promijeniti:

32 x 13 = 16 x 26 = 8 x 52 = 4 x 104 = 2 x 208 = 1 x 416

Zanimljivo je da je ova metoda umnožavanja bila poznata u Rusiji, a smatralo se da je došlo iz drevnog Egipta, au Europi je nazvano ruskim.

Papyrus Golenishcheva

Zahvaljujući naporima znanstvenika egiptologa V. S. Golenischeva, papirus je pohranjen u Moskvi još 200 godina stariji od papirusa pisara Ahmesa. Znanstvenik ga je kupio tijekom svog rada u Tebi.

Napisana je hijeratski, u kurzivu, bavi se 25 problemima, dan je njihov opis prema egipatskom brojevnom sustavu i rješenje. Njegova je duljina veća od 5 m, a širina je 7 cm. Na ove probleme nema komentara, kao u prethodnom papirusu, postoje samo matematički izračuni.

To pokazuje da su Egipćani mogli s velikom točnošću izračunati površine trokuta, trapeza, pravokutnika, kruga, kao i volumena piramide, prizme, paralelepipeda, cilindra i krnje piramide, a mnoge formule u potpunosti se podudaraju s modernim.

U egipatskom brojevnom sustavu broj pi je bio 3,16, što je gotovo odgovaralo modernoj vrijednosti 3,14, iako je u to vrijeme vrijednost 3 bila korištena svugdje na Istoku.

Sve su stvari brojke

Smatra se da je Pitagora živio u Egiptu već 22 godine, duboko proučavajući geometriju, filozofiju, misticizam brojeva. Ta otkrića koja je kasnije napisana u pitagorejskoj školi mogla su biti napravljena u starom Egiptu.

Stoga se vjeruje da se djela Pitagore o misticizmu brojeva koje je kasnije napisao temelje na tajnom znanju koje je dobio od egipatskih svećenika. Nisu uzimali strance na studij, on je došao do njih po visokom pokroviteljstvu, nakon razgovora s glavnim svećenikom, koji je smatrao dostojnim da bude upućen u tajne.

Brojevi su bili živa bića, odražavajući svojstva prostora, glazbe, energije. Sve se može izraziti kroz matematiku, opisujući vidljive fenomene formulama, predvidjeti nevidljivo, na temelju logike i matematičkih zakona.

Visina, širina podnožja, kut nagiba Keopsove piramide u Egiptu one odgovaraju matematičkom pravilu za izgradnju pitagorejske piramide, što također potvrđuje povezanost otkrića koja je on napravio i znanje stečeno od drevnih egipatskih svećenika koji su koristili egipatski sustav brojeva.

Radeći s brojevima, drevni mislioci ne samo da su razumjeli suštinu stvari, već su mogli utjecati i na njih.

Proučavajući matematiku drevnog Egipta, koristeći se egipatskim brojevnim sustavom, možemo se samo diviti koliko su ljudi otkrili tisuće godina prije naše ere.