Što je integral? Integrali s detaljnim rješenjem. Integralna tablica
Riječ "integral" dolazi od latinske integralis - holističke. Ovaj naslov je predložen u 17. stoljeću. student velikog Leibniza (i također izvanredan matematičar) I. Bernoulli. A što je integralni u suvremenom smislu? U nastavku ćemo pokušati dati sveobuhvatan odgovor na ovo pitanje.
Povijesna pozadina pojma integral
Početkom 17. stoljeća u razmatranju vodećih znanstvenika došlo je do velikog broja fizičkih (prije svega mehaničkih) zadataka u kojima je bilo potrebno istražiti ovisnosti pojedinih količina o drugima. Najočitiji i najhitniji problemi bili su određivanje trenutne brzine nejednakog kretanja tijela u bilo kojem danom trenutku i njegov obrnuti problem pronalaženja veličine puta koji je tijelo prolazilo tijekom određenog vremenskog razdoblja tijekom takvog kretanja. Danas već znamo što je integral brzine kretanja - to je put koji putuje. Ali razumijevanje kako ga izračunati, poznavanje brzine u svakom trenutku u vremenu, nije se odmah pojavilo.
Isprva, iz razmatranja takvih ovisnosti fizikalnih veličina, na primjer o putanji na brzini, nastao je matematički koncept funkcije y = f (x). Proučavanje svojstava različitih funkcija dovelo je do pojave matematička analiza. Znanstvenici aktivno traže načine za proučavanje svojstava različitih funkcija. 
Kako je izračun integrala i derivata?
Nakon što je Descartes stvorio osnove analitičke geometrije i grafički prikazao funkcionalne ovisnosti o osi kartezijanskog koordinatnog sustava, istraživači su se susreli s dva nova zadatka: kako nacrtati tangentu na zakrivljenu liniju u bilo kojoj točki i kako pronaći područje figure iznad ove krivulje i ravne linije, paralelno s koordinatnim osima. Na neočekivan način, ispostavilo se da je prvi jednak pronalaženju trenutne brzine, a drugi od pronalaženja pređene udaljenosti. Uostalom, u slučaju neujednačenog kretanja, on je prikazan u kartezijanskim osima koordinata "udaljenost" i "vrijeme" s određenom zakrivljenom linijom.
Genij Leibniz i Newton sredinom 17. stoljeća. stvorene su metode koje omogućuju rješavanje oba problema. Pokazalo se da je za provođenje tangente na krivulju u određenoj točki potrebno pronaći vrijednost tzv. Izvedenice funkcije koja opisuje tu krivulju u točki o kojoj se radi, a ta je vrijednost jednaka brzini promjene funkcije, tj. U odnosu na ovisnost o putanji u odnosu na brzinu. trenutna brzina tijela.
Da bi se pronašlo područje ograničeno krivuljom, bilo je potrebno izračunati određeni integral, koji je dao njegovu točnu vrijednost. Derivativni i integralni - osnovni pojmovi diferencijalnog i integralnog računa koji su temelj moderne matematičke analize - najvažniji dio više matematike.
Područje ispod krivulje
Dakle, kako ga definirati točnu vrijednost? Pokušajmo od samog početka detaljno otkriti proces njegovog izračuna kroz integral.
Neka je f kontinuirana funkcija na intervalu [ab]. Razmotrite krivulju y = f (x) prikazanu na slici ispod. Kako pronaći područje površine ograničeno krivuljom), x osi i linije x = a i x = b? To jest, područje zasjenjene figure na slici. 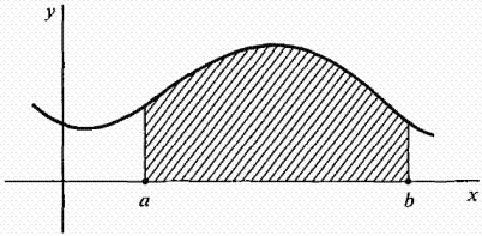
Najjednostavniji slučaj je kada je f konstantna funkcija; to jest, krivulja je vodoravna crta f (X) = k, gdje je k konstanta i k ≥ 0, kao što je prikazano na slici ispod. 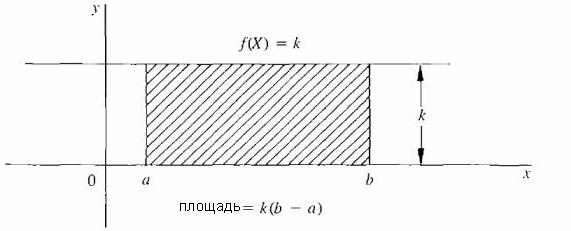 U ovom slučaju, površina ispod krivulje je samo pravokutnik s visinom k i širinom (b - a), tako da je područje definirano kao: k · (b - a).
U ovom slučaju, površina ispod krivulje je samo pravokutnik s visinom k i širinom (b - a), tako da je područje definirano kao: k · (b - a).
Područja nekih drugih jednostavnih oblika, kao što su trokut, trapez i polukrug, dana su planimetričkim formulama.
Područje pod bilo kojom kontinuiranom krivuljom y = f (x) dano je određenim integralom, koji je ispisan na isti način kao i regularni integral.
Riemannova suma
Prije nego što se upustimo u detaljan odgovor na pitanje što je integral, istaknimo neke osnovne ideje.
Prvo, područje ispod krivulje podijeljeno je na određeni broj n vertikalnih pruga dovoljno male širine Δx. Nadalje, svaka vertikalna traka se zamjenjuje okomitim pravokutnikom visine f (x), širine Δx i površine f (x) dx. Sljedeći korak je formiranje zbroja područja svih ovih pravokutnika, koji se nazivaju Riemannova suma (vidi donje slike).
Crtanjem naših pravokutnika xx široko, možemo uzeti njihovu visinu jednaku vrijednosti funkcije na lijevom rubu svake trake, tj. Krivulja će biti krajnje lijeve točke njihovih gornjih kratkih strana Δx široke. U isto vrijeme, u dijelu gdje funkcija raste, a njegova krivulja je konveksna, svi pravokutnici su ispod te krivulje, tj. Njihova suma će sigurno biti manja od točne vrijednosti površine ispod krivulje u ovom području (vidi sliku dolje). Ova metoda aproksimacije naziva se lijevom stranom. 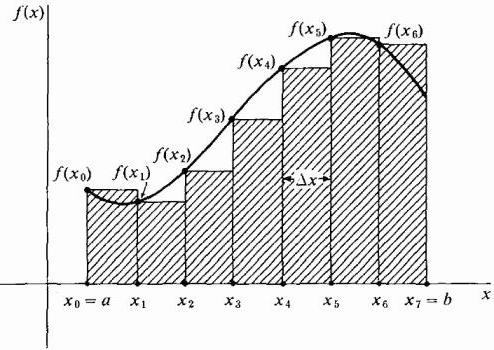
U principu, moguće je nacrtati aproksimirajuće pravokutnike na takav način da ekstremne desne točke njihovih gornjih kratkih strana širine Δx leže na krivulji. Tada će biti veći od krivulje, a aproksimacija područja u ovom području bit će veća od njezine točne vrijednosti, kao što je prikazano na donjoj slici. Ova metoda se zove pravo. 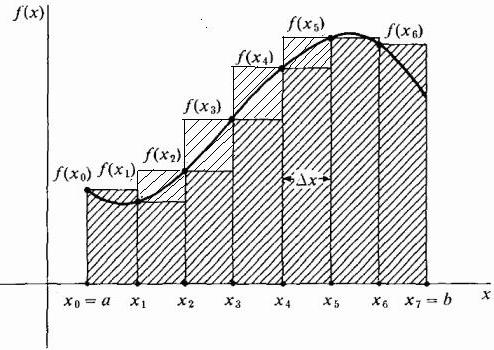
Ali možemo također uzeti visinu svakog od aproksimiranih pravokutnika jednakim samo nekoj vrijednosti funkcije u proizvoljnoj točki x * i unutar odgovarajuće trake Δx i (vidi sl. nastavku). U ovom slučaju, čak ne možemo uzeti istu širinu svih traka. 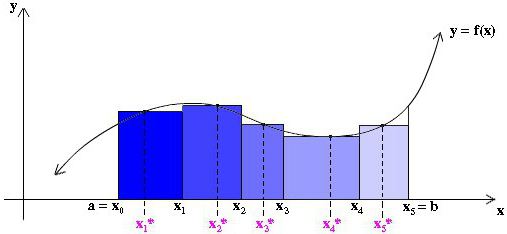
Izrađujemo Riemannov iznos:

Prijelaz iz Riemannove suma u definitivni integral
U višoj matematici dokazan je teorem, koji kaže da ako, s neograničenim povećanjem broja n aproksimiranih pravokutnika, njihova najveća širina teži nuli, tada Riemannova suma A n teži prema nekoj granici A. Broj A je isti za bilo koji način oblikovanja aproksimacija pravokutnika i za bilo koji izbor točaka x * i .
Jasno objašnjenje teorema dano je na slici ispod.
To pokazuje da, što su uži pravokutnici, to je područje stepenastog broja bliže području ispod krivulje. Kada je broj pravokutnika n → ∞, njihova širina je Δx i → 0, a granica A zbroja A n je brojčano jednaka traženoj površini. Ovo ograničenje i postoji određeni integralni dio funkcije f (x): 
Integralni simbol, koji je modificirani kurziv S, uveo je Leibniz. J. B. Fourier je predložio da se oznaka za integral stavi na vrh i na dno. Istovremeno su jasno naznačene početne i konačne vrijednosti x.
Geometrijska i mehanička interpretacija određenog integrala
Pokušajmo dati detaljan odgovor na pitanje što je integralni? Razmotrimo integral na intervalu [a, b] iz pozitivne funkcije f (x) unutar njega i pretpostavimo da je gornja granica veća od donje Ako su ordinate funkcije f (x) negativne unutar [a, b], tada je apsolutna vrijednost integrala jednaka površini između x-osi i grafa y = f (x), a sam integral je negativan. U slučaju jednokratnog ili ponovljenog sjecišta y = f (x) osi apscise na segmentu [a, b], kako je prikazano na donjoj slici, za izračunavanje integrala potrebno je odrediti razliku u kojoj je smanjenje jednako ukupnoj površini ploha iznad x-osi , i odbitna - ukupna površina područja ispod nje. Mehanička interpretacija određenog integrala usko je povezana s geometrijskim. Vratimo se na odjeljak "Riemannova suma" i zamislimo da grafikon prikazan na slikama izražava funkciju brzine v = f (t) s nejednolikim kretanjem materijalna točka (osa apscise je vremenska os). Tada će površina bilo kojeg aproksimiranog pravokutnika širine Δt, koju smo izgradili za vrijeme stvaranja Riemannove sume, izraziti približno put točke u vremenu Δt, odnosno v (t *) Δt. Ukupna suma površina pravokutnika na intervalu od t 1 = a do t 2 = b izražava približno put s u vremenu t 2 - t 1 i njezina granica, tj. integralni (definirani) od a do b funkcije v = f (t) iznad dt će dati točnu vrijednost puta s. Ako se vratimo na njegovu oznaku, onda možemo dobro pretpostaviti da je a = const, a b specifična vrijednost neke nezavisne varijable x. Tada se određeni integral s gornjom granicom x̃ iz konkretnog broja pretvara u funkciju od x̃. Takav integral je jednak površini slike ispod krivulje označene točkama aABb na donjoj slici. Pretpostavimo da smo dali varijablu x̃ = b neki mali prirast ̃x̃. Tada se prirast površine figure aABb sastoji od područja pravokutnika (zasjenjenog na slici) Bb ̃ Δx̃ i površine BDC figure ispod krivulje. Područje pravokutnika jednako je Bb x Δx f = f (x̃) Δx̃, to jest, to je linearna funkcija prirasta nezavisne varijable. Područje BDC oblika je očito manje od područja pravokutnika BDCK = Δx̃ ∙ Δy, a kako Δx̃ → 0 teži, on se smanjuje čak i brže od njega. Dakle, f (x̃) Δx̃ = f (x̃) dx̃ je razlika varijabilnog područja aABb, tj. Diferencijala određenog integrala Iz toga možemo zaključiti da se izračunavanje integrala sastoji u pronalaženju funkcija iz danih izraza njihovih diferencijala. Integralni račun upravo je sustav metoda za pronalaženje takvih funkcija iz njihovih poznatih diferencijala. Ona povezuje odnos između diferencijacije i integracije i pokazuje da postoji operacija inverzna prema diferencijaciji funkcije - njenoj integraciji. Također pokazuje da ako je bilo koja funkcija f (x) kontinuirana, tada primjenom te matematičke operacije na nju možete naći cijeli skup (skup, skup) funkcija primitivnih za njega (ili na drugi način pronaći neodređeni integralni od njega). Neka je funkcija F (x) oznaka rezultata integriranja funkcije f (x). Korespondencija između ove dvije funkcije kao rezultat integracije druge od njih naznačena je kako slijedi: Kao što se može vidjeti, s integralnim simbolom nema ograničenja integracije. To znači da se iz određenoga transformira u neodređeni integralni. Riječ "neodređeno" znači da rezultat operacije integracije u ovom slučaju nije jedna, nego mnoge funkcije. Doista, osim same funkcije F (x), svaka funkcija F (x) + C zadovoljava posljednje izraze, gdje je C = const. To podrazumijeva da se stalni član u skupštini antiderivativa može proizvoljno postaviti. Treba naglasiti da ako je integral definiran funkcijom broj, onda je neodređeno funkcija, točnije, njihov skup. Pojam "integracija" koristi se za definiranje potrage za oba tipa integrala. To je potpuna suprotnost odgovarajućeg pravila za diferencijaciju. Kako se uzimaju neodređeni integrali? Primjeri ovog postupka razmatramo specifične funkcije. Pogledajmo funkciju snage općeg oblika: f (x) = cx n Nakon što smo to učinili sa svakim izrazom u izrazu integrabilne funkcije (ako ih ima više), dodamo konstantu na kraju. Podsjetimo se da ga uzimanje derivata konstantne vrijednosti uništava, tako da uzimanje integrala bilo koje funkcije daje nam obnovu ove konstante. Označavamo ga s C, jer je konstanta nepoznata - može biti bilo koji broj! Stoga možemo imati beskonačno mnogo izraza za neodređeni integral. Pogledajmo jednostavne neograničene integrale, primjeri koji su prikazani ispod. Pretpostavimo da trebate pronaći integralni dio funkcije: f (x) = 4x2 + 2x - 3. Počnimo s prvim pojmom. Pogledamo eksponent 2 i povećamo ga za 1, zatim prvi pojam dijelimo s rezultirajućim pokazateljem 3. Dobivamo: 4 (x 3 ) / 3. Tada ćemo pogledati sljedećeg člana i učiniti isto. Budući da ima eksponent 1, rezultirajući pokazatelj će biti 2. Dakle, taj pojam dijelimo s 2: 2 (x 2 ) / 2 = x 2 . Posljednji izraz ima faktor x, ali ga jednostavno ne vidimo. Posljednji izraz možemo zamisliti kao (-3x 0 ). To je ekvivalentno (-3) ∙ (1). Ako koristimo pravilo integracije, dodamo 1 indikatoru kako bismo ga podigli na prvi stupanj, a onda podijelimo posljednji izraz na 1. Dobivamo 3x. Ovo pravilo integracije radi za sve vrijednosti n, osim n = - 1 (jer ne možemo dijeliti s 0). Smatrali smo najjednostavniji primjer pronalaženja integralnog. Općenito, rješenje integrala nije lak zadatak, a iskustvo koje je već stečeno u matematici u tome je dobra pomoć. U gornjem dijelu vidjeli smo da se iz svake formule diferencijacije dobiva odgovarajuća integracijska formula. Stoga su sve njihove moguće opcije već davno dobivene i sažete u odgovarajućim tablicama. Sljedeća tablica integrala sadrži formule za integriranje osnovnih algebarskih funkcija. Te formule treba pamtiti, pamtiti ih postupno, jer su fiksne vježbe. Druga tablica integrala sadrži glavne trigonometrijske funkcije: Ispostavlja se da je za to moguće jednostavno integrirati se, tj. Pronaći neodređene integrale. I formula osnivača Newton-Leibnizova integro-diferencijalnog računa pomaže u tome. Prema tome, u prvoj fazi izračun željenog integrala sastoji se u pronalaženju neodređenog, zatim izračunavanju vrijednosti pronađenog primitivnog F (x) uz zamjenu x, jednakoj gornjoj granici, zatim prema nižoj, i konačno, za određivanje razlike tih vrijednosti. U ovom slučaju konstanta C se ne može napisati. jer nestaje pri izuzimanju. Neke integrale razmatramo s detaljnim rješenjem. Pronađite područje mjesta pod jednim sinusnim valom od pola vala. Sada razmatramo integrale s detaljnim rješenjem koje koristi svojstvo aditivnosti u prvom primjeru, te zamjenu varijable intermedijarne integracije u drugom primjeru. Izračunavamo određeni integralni dio djelomično racionalne funkcije: y = (1 + t) / t 3 od t = 1 do t = 2. Sada ćemo pokazati kako pojednostaviti uzimanje integrala uvođenjem intermedijerne varijable. Pretpostavimo da trebate izračunati integral od (x + 1) 2 . Govorili smo o određenom integralu za konačni interval [a, b] funkcije f (x) kontinuiranog na njoj. Međutim, određeni broj specifičnih problema dovodi do potrebe da se koncept integrala proširi na slučaj kada su granice (jedna ili obje) jednake beskonačnosti, ili kada je diskontinuirana funkcija. Primjerice, kada se računaju površine ispod krivulja, asimptotski se približavaju osi koordinata. Da bi se koncept integrala proširio na ovaj slučaj, uz prolaz do granice u izračunavanju Riemannovog zbroja aproksimiranih pravokutnika, izvodi se još jedan. S takvim dvostrukim prolazom do granice dobiva se neispravan integral. Nasuprot tome, svi gore navedeni integrali nazivaju se pravilnim. 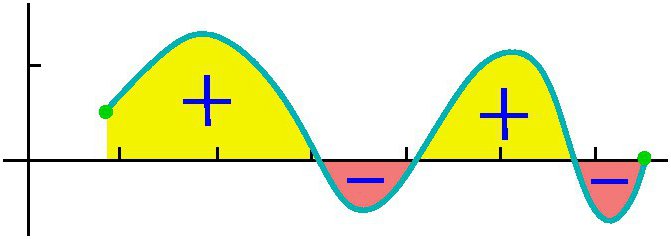 Dakle, za funkciju prikazanu na slici iznad, određeni integral od a do b će biti (S1 + S3) - (S2 + S4).
Dakle, za funkciju prikazanu na slici iznad, određeni integral od a do b će biti (S1 + S3) - (S2 + S4). Diferencijal određenog integrala
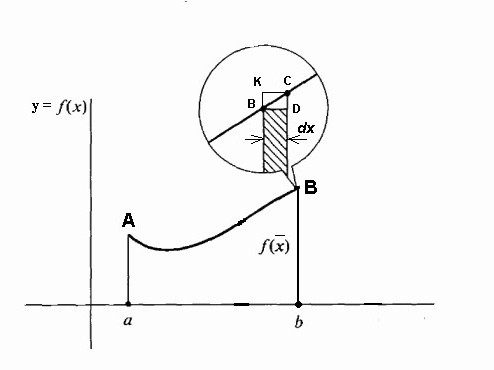 S fiksnom linijom aA i pokretnim Bb, ovo područje postaje funkcija f (x̃), pri čemu se inkrementi Δx̃ još uvijek talože duž x osi, a inkrementi funkcije f (xments) su inkrementi površine ispod krivulje.
S fiksnom linijom aA i pokretnim Bb, ovo područje postaje funkcija f (x̃), pri čemu se inkrementi Δx̃ još uvijek talože duž x osi, a inkrementi funkcije f (xments) su inkrementi površine ispod krivulje. 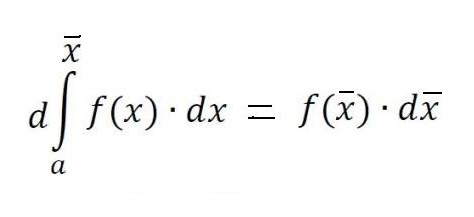
Temeljni omjer integralnog računa
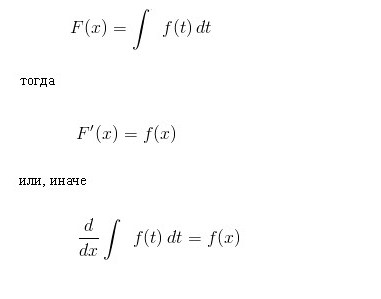
Osnovno pravilo integracije

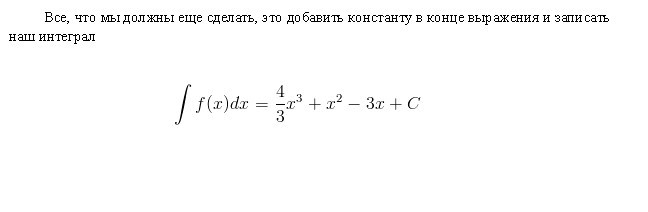

Integralne tablice
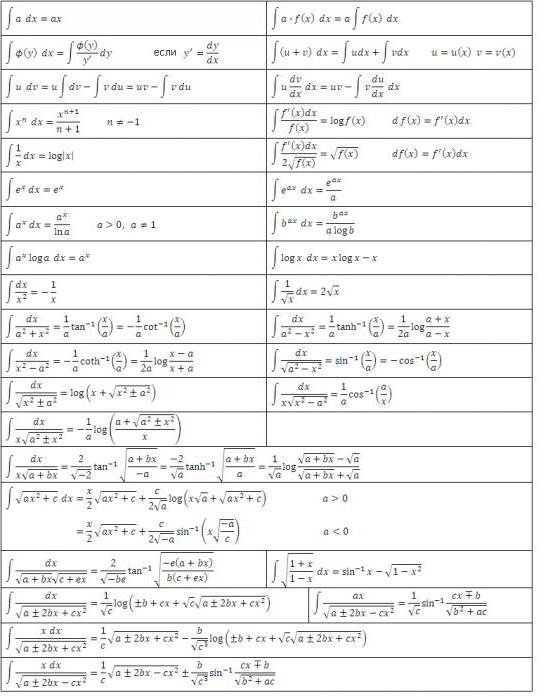

Kako izračunati određeni integral
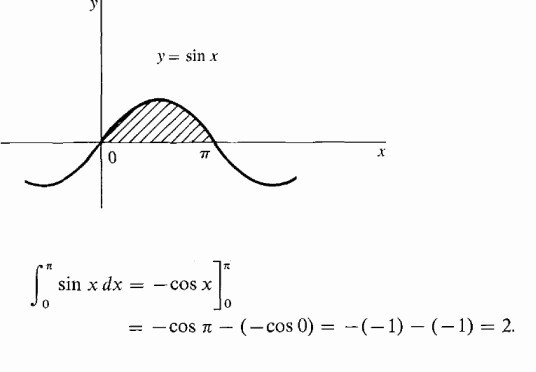 Izračunajte zasjenjeno područje pod hiperbolom.
Izračunajte zasjenjeno područje pod hiperbolom. 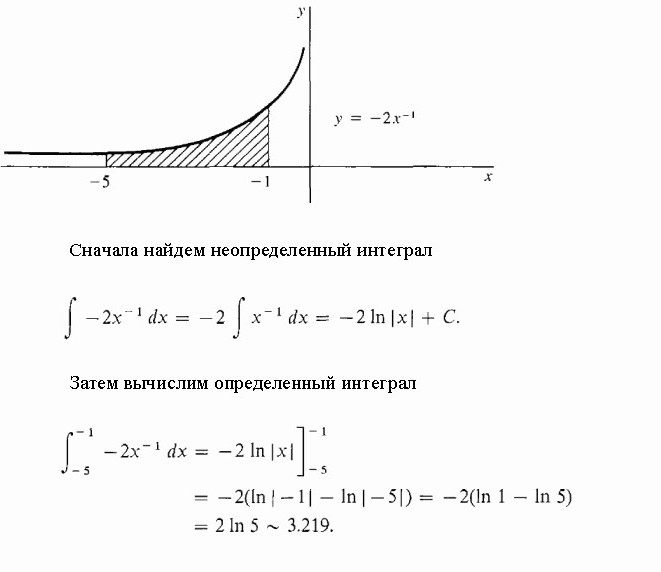
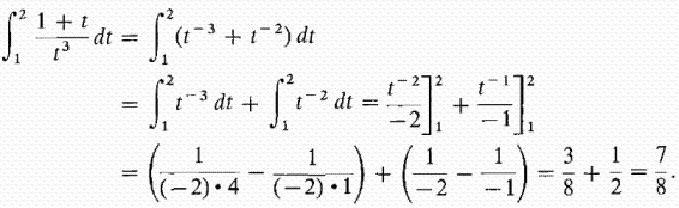
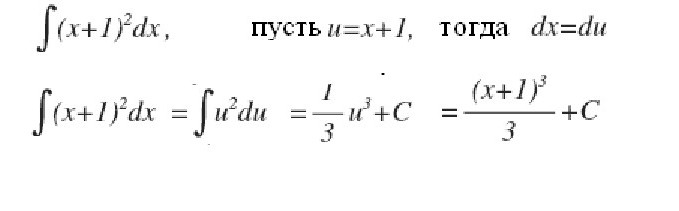
O nepropisnim integralima