Koji je trenutak izmjerene inercije, koje je njegovo fizičko značenje?

Rotacija mehaničkog sustava jedan je od najčešćih načina kretanja tijela u prostoru. Ovaj tip kretanja karakterizira skup fizičkih veličina, čije ime sadrži riječ "trenutak". Ovaj je članak posvećen odgovaranju na sljedeće pitanje: u kojem se trenutku mjeri inercija?

Karakteristika rotacije

Svi su svjesni onoga što je u pitanju. Dovoljno je spomenuti rotaciju kotača automobila, bicikla ili kotača u zabavnom parku. Ako govorimo o velikim prostorima i masama, možemo se prisjetiti rotacije naše Zemlje oko zvijezde Sunca.

U fizici, sva pomicanja objekata zabilježena u gornjim primjerima obično se opisuju sljedećom jednadžbom:

M¯ = dL¯ / dt.

Ovdje je M trenutak vanjske sile, koja, djelujući na sustav tijekom vremena dt, uzrokuje promjenu kutnog momenta za vrijednost dL. Stupac iznad znakova označava da su to vektori.

Ako vanjske sile nemaju nikakav trenutak M¯p, tada gornja jednadžba postaje takozvani zakon očuvanja kutnog momenta L¯, to jest:

L¯ = const.

Kutni moment (koji se naziva i kutni moment) unosi se u fiziku kao vektorski proizvod linearnog momenta točke s masom m i brzine v¯ i vektora r¯, koji je okomit na os rotacije i povezuje ga s tom točkom, odnosno:

L¯ = r¯ * m * v¯.

Ako upotrijebimo pojam kutne brzine ω¯ i njenu vezu sa sličnom linearnom veličinom v, tada se ta jednakost može ponovno napisati u ovom obliku:

L¯ = I * ω¯.

U ovom izrazu, I je faktor koji povezuje dvije vektorske veličine. Dobio je ime trenutka inercije.

Magnituda i u fizici

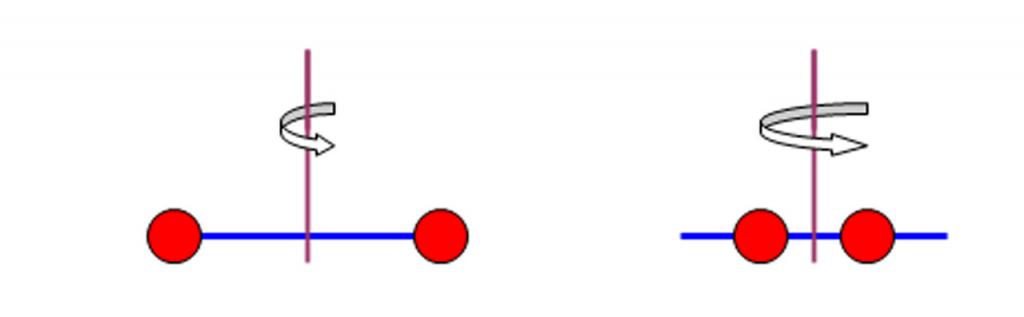
U zadnjem izrazu prethodnog stavka, vrijednost I jednaka je proizvodu mase točke po kvadratu njezine udaljenosti od osi, odnosno:

I = m * r2.

Budući da sva stvarna tijela nisu materijalne točke, već imaju određene prostorne parametre i oblik, za određivanje njihovog momenta inercije koristi se izvorni izraz koji postaje integrand. Opća formula za tijelo I je sljedeća:

I = ( _m (r2 * dm).

Ova matematička formula kaže da je za izračun trenutka inercije cijelog tijela potrebno mentalno ga podijeliti u materijalne točke dm, pomnožiti ih s kvadratom udaljenosti do osi rotacije, a zatim dodati sve rezultate.

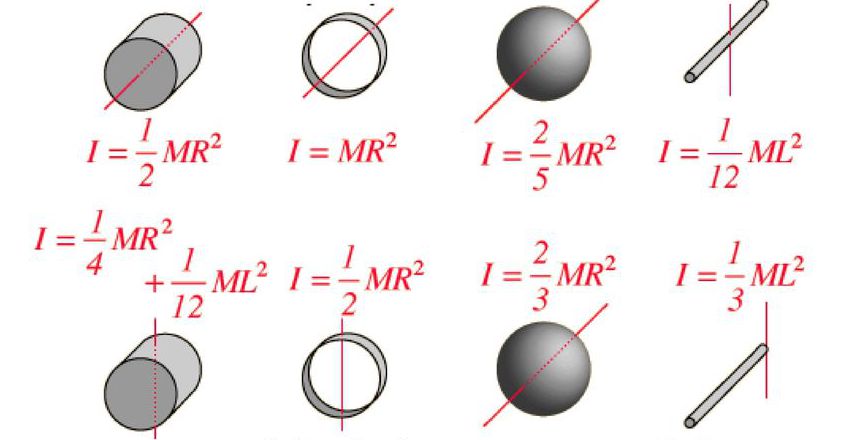
Kako se mjeri trenutak inercije tijela?

Budući da je gore navedeno osnovna informacija koju morate znati da biste razumjeli vrijednost o kojoj se radi, svatko može odgovoriti na pitanje o ovoj stavci. Ipak, razmatramo ga detaljnije.

Dakle, u kojim jedinicama se mjeri trenutak inercije tijela? I formula za materijalnu točku i opći izraz za tijelo proizvoljnog oblika vode do istog odgovora: vrijednost I apsolutno bilo kojeg rotirajućeg sustava mjeri se u kilogramima po kvadratnom metru (kg * m2).

Naravno, da bi se izrazio trenutak inercije, možete koristiti bilo koje djelomične jedinice od navedenog standarda u SI. Na primjer, za sustave s malim masama i linearnim dimenzijama, I se može izraziti u gramima po centimetru na kvadrat (g * cm2). Naprotiv, megatoni se mogu koristiti na kozmičkim ljestvicama za astronomske jedinice u kvadratu (najčešće se ipak koristi kg * m ² s brojem 10, izgrađenim u velikoj mjeri).

Odgovarajući na pitanje kako se mjeri trenutak inercije, treba spomenuti drugačiji pristup kako bi se izrazila ta količina. Da bismo ga razumjeli, napišemo formulu za promjenu kutnog momenta:

M¯ = dL¯ / dt = I * dω¯ / dt, dakle, I = M¯ * dt / dω¯.

Kako se trenutak sila mjeri u newtonima po metru (N * m), dt - u sekundama, dω¯ - u radijanima u sekundi, dobivamo za I:

I = [N * m * s ² / rad] ili [J * s ² / rad].

Obje mjerne jedinice vrijede za I, ali gotovo da se ne koriste u rješavanju problema, jer su izvedene iz standarda u SI, odnosno od kg * m ² . Ipak, ove su jedinice (posebno potonje) povezane s fizičkim značenjem procesa rotacije tijela.

Znači ja

Razmatrajući pitanje jedinica u kojima se mjeri moment inercije, možemo reći i što to znači.

Ako obratimo pozornost na oblik bilježenja kutnog momenta L¯ kroz brzinu ω¯, tada možemo uočiti njegovu potpunu sličnost s izrazom za linearni impuls. Iz te sličnosti slijedi da je moment inercije I neka vrsta mase za kretanje rotacije. Što više ja, to je teže ubrzati sustav (okretati ga ili zaustavljati).

S obzirom na fizičko značenje I sa stajališta energije, okrenimo se mjernoj jedinici dobivenoj u prethodnom odlomku - [J * s ² / rad]. To pokazuje da je za moment inercije tijela pri 1 J * s ² / rad (1 kg * m ² ) potrebno da trenutak sila radi na 1 J da bi se sustavu dalo kutno ubrzanje jednako 1 rad / s2.

Odjeljak momenta inercije

Odgovarajući na pitanje kako se mjeri moment inercije, smatrali smo vrijednost I za rotirajuće tijelo. Ipak, postoji još jedna količina, koja se u matematici naziva momentom inercije drugog reda. To je sasvim drugačija vrijednost od razmatrane. Izračunava se preko dvostrukog integrala za proizvoljni poprečni presjek i koristi se za analizu napona pri savijanju koje nastaju u stvarnim tijelima kada su izložena vanjskim opterećenjima. Ovaj moment inercije mjeri se u jedinicama duljine do četvrte snage, tj. U m ⁴ .